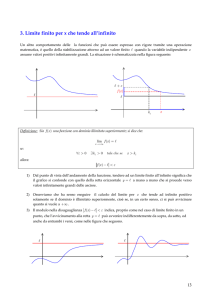
Esempio: analizza il limite per x che tende a c=2
LIMITI
y
Ord =limite
Sia y=f(x) funzione
definita in dominio D.
Ord =limite
Sia c ∉D
c
Cercare il LIMITE della funzione
per x→c ( x che tende a c) significa trovare,
man mano che la x TENDE a c,
l’ORDINATA
a cui SI AVVICINA la funzione.
Per x→2 - da sinistra
le ordinate tendono
a l =3 dal basso
CI SONO QUATTRO DEFINIZIONI DI LIMITE
1) LIMITE FINITO l per x→c valore finito
Man mano che la x tende a c da sin e da ds
le ordinate tendono al valore finito
l
# lim" f (x) = 3"
% x!2
$
lim+ f (x) = 3+
%& x!2
Lim sinistro
Lim destro
Quando limite sin = lim destro
lim f(x)= ∞
x→c
l
x
LIMITE destro
Per x→c + le ordinate
possono tendere a l
o dall’alto o dal basso
Man mano che la x tende a ±∞
lim f(x)= l
x→∞
le ordinate tendono a l
l
-∞
←
LIMITE destro di c
x
Analogo ragionamento per x→c+
x=c è asintoto verticale
In figura è rappresentata una della 4 possibili situazioni
4) LIMITE INFINITO per x che tende all’infinito
lim f(x)= ∞
Man mano che la x tende a ±∞
le ordinate tendono a ±∞
x→∞
y= l asintoto orizzontale
→
Per x→c- le ordinate possono tendere
o a + ∞ (divergono positivamente)
oppure a -∞ ( div negativamente)
(uno dei due casi)
c
y
_
_
_
LIMITE sinistro di c
→ ←
In figura è rappresentata una della 4 possibili situazioni
3 ) LIMITE FINITO l per x che tende all’infinito
LIMITE verso meno infinito
Per x→ -∞
le ordinate possono tendere
y
+∞
x
LIMITE sinistro di infinito
Per x→ -∞ le ordinate possono tendere
o a l+ (dall’ alto) oppure a a l- (dal basso)
Analogamente per x→ +∞ ( limite destro di infinito)
In figura è rappresentata una della 4 possibili situazioni
x!2
Man mano che la x -->c [da sin e da ds ]
le ordinate tendono all’ infinito ±∞
y
c
lim f (x) = 3
2) LIMITE INFINITO per x→c: valore finito
y
LIMITE sinistro
Per x→c - le ordinate
possono tendere a l
o dall’alto o dal basso
(uno dei due casi)
Per x→2 + da destra
le ordinate tendono
a l =3 dall’alto
2
Si scrive in forma compatta:
Tutorial di Paola Barberis - agg 2012
lim f(x)= l
x→c
l=3
←
-∞
→
o a +∞ (divergono positivamente)
oppure a -∞ ( div negativamente)
+∞
x
Analogamente per x→ +∞
In figura è rappresentata una della 4 possibili situazioni
1
es
em
pi
funzione esponenziale con base e:
Analizza i limiti agli estremi del dominio
y=ex
Dominio: ∀x∈R (- ∞;+∞)
Codominio COD: y>0
Gli estremi del dominio sono - ∞ ;+∞
y=
ex
x
es
em
pi
Funzione logaritmica con base e :
Analizza i limiti agli estremi del dominio
y=lnx
Gli estremi del dominio sono
lim e x = e-∞ =0+
x→-∞
lim e x = e+∞=+∞
x→+∞
F. Log con base maggiore di 1
F. Log con base compresa tra 0 e 1
Asintoto verticale: x=0 (asse y)
Limiti: principali regole di calcolo
+! + 5 = +!
"! + 7 = "!
#log(0 + ) = +!
$
%log(+!) = "!
#log(0 + ) = !"
$
%log(+") = +"
F. esp con base maggiore di 1
!"
+
%#a = 0
$ +"
&%a = +"
"! " ! = "!
+! + ! = +!
( +! ) # ( +7 ) = +!
( +! ) # ( "5 ) = "!
F. esp con base compresa tra 0 e 1
!"
%#a = +"
$ +"
+
&%a = 0
CALCOLO di Limiti
Il calcolo di un limite si ottiene, per funzioni
continue, sostituendo
il valore a cui tende la x nella funzione f(x):
0+ ;+∞
lim ln x = ln(0+ ) = -∞
x→0 +
lim ln x = ln(+∞)= +∞
x→+∞
Asintoto orizzontale
(asse x): y=0
Riepilogo LIMITI FUNZ ESPONENZIALE E LOGARITMICA
Dominio D: x>0 (0;+∞)
Codominio COD: ∀ y ∈ R
0
=0
N
!
=!
N
BASE > 1
opp _ BASE = e
e
!"
=0
+
e!" = +"
ln0 + = !"
ln ( +" ) = +"
0 < BASE < 1
a !" = +"
a +" = 0 +
+
log 0 = +"
log ( +" ) = !"
a
a
Quando il denominatore tende ad infinito
ATTENZIONE N " 0
l’intera frazione tende a ZERO
!
Quando il denominatore tende a zero
N
"!
l’intera frazione tende ad INFINITO
0
Forme indeterminate +∞ -∞ ∞ / ∞
0 / 0 0·∞
Principali Forme indeterminate:
+! " !
!
!
0
0
come eliminarle
Raccolgo la x di grado massimo
Il risultato è +∞ oppure -∞
Rapporto dei termini di grado max al Num e Den
LIMITE IMMEDIATO
Se ottengo subito il
risultato finito o
infinito, il limite si
chiama IMMEDIATO
LIMITE CON FORMA
INDETERMINATA
Se ottengo una di queste
forme indeterminate:
+∞ -∞ ∞ / ∞
0/0
In tal caso si deve“ togliere”
l’indeterminazione
Se gradoNUM>gradoDEN ottengo limite ∞
Se gradoNUM =gradoDEN ottengo limite finito l
Se gradoNUM<gradoDEN ottengo 0
Devo scomporre numeratore e denominatore
o con le note regole o con il metodo di Ruffini
Otterrò un fattore che si semplifica mandando via
l’indeterminazione.
Il risultato può essere finito o infinito
2