MATEMATICA
LEZIONE 9
POTENZE DI NUMERI RELATIVI
(Prof. Daniele Baldissin)
ARGOMENTI
1) Definizione di potenza di un numero relativo
2) Le proprietà delle potenze (un ripasso)
Prendiamo un numero relativo che chiameremo a. Ora supponiamo che il numero n sia un numero
intero positivo (esempio +1, +2, + 3, +4, ecc..). Chiameremo potenza n-essima (si legge
ennesima) di a il prodotto di n fattori uguali ad a.
Questa potenza si rappresenta col simbolo an.
Esso sta ad indicare che dobbiamo moltiplicare a per se stesso n volte.
Esempio:
(+2)3 = (+2) x (+2) x (+2)
(-5)4 = (-5) x (-5) x (-5) x (-5)
(-3)5 = (-3) x (-3) x (-3) x (-3) x (-3).
Il numero a prende il nome di base, mentre n si dice esponente o grado della potenza.
Per convenzione si ha che:
a1 = a
mentre
a0 = 1 a condizione che a sia diverso da zero, cioè
0
avremmo 0 che non ha significato.
. Infatti, se a fosse uguale a zero,
Ricapitolando:
a
n
an
a
n
a1
a0
NUMERO RELATIVO
NUMERO INTERO POSITIVO
potenza n-essima di a (si legge potenza
ennesima di a)
significa moltiplicare a per se stesso per n
volte
BASE
ESPONENTE
=a
=1
Vediamo ora come si esegue la potenza di un numero relativo, posto che n sia un numero intero
positivo (delle potenze di numeri relativi con esponente negativo parleremo in seguito).
La potenza del numero relativo an si determina nel modo seguente:
il suo valore assoluto si ottiene moltiplicando il valore assoluto per se stesso per n volte.
il suo segno sarà positivo se l'esponente è pari, mentre risulterà invariato rispetto al
segno della base se l'esponente è dispari.
Cioè:
an
a x a x a ...... (per n volte)
valore
assoluto
Esempio:
(+2)3
valore assoluto del risultato: 2 x 2 x 2 = 8
positivo se n è pari
Esempio:
segno
(+2)2
valore assoluto del risultato: 2 x 2 = 4
segno: n = 2; pari; segno +
(+2)2 = +4
invariato se n è dispari
Esempio:
(+2)3
valore assoluto del risultato: 2 x 2 x 2 = 8
segno: n = 3; dispari; segno uguale a quello
della base, cioè +
(+2)3 = +8
La potenza gode delle stesse proprietà delle potenza proprie dell'aritmetica. Le ricordiamo di
seguito. Esse sono importanti perchè permettono di semplificare numerosi calcoli.
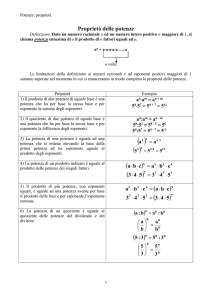
PRIMA PROPRIETA’
Il prodotto di due o più potenze aventi la stessa base è una potenza della stessa base con
esponente uguale alla somma degli esponenti.
Quindi:
am an = a m+n
POSITIVI.
- ponendo come condizione che m ed n siano NUMERI INTERI
Esempio:
(-2)2 (-2)3 = (4) (-8) = 32.
Come possiamo notare la base dei due fattori del prodotto è la stessa (-2).
Ora proviamo ad applicare la regola precedente. Avremo:
Come possiamo osservare il risultato è uguale.
SECONDA PROPRIETA’
Il quoziente di due o più potenze aventi la stessa base è una potenza della
stessa base con esponente uguale alla differenza degli esponenti.
Quindi:
am : an = a m-n
ponendo come condizione che m sia maggiore di n (si scrive m > n).
Esempio:
(3)4 : (3)3 = 81 : 27 = 3.
Come possiamo notare la base del dividendo e del divisore è la stessa (pari a 3).
Ora proviamo ad applicare la regola precedente. Avremo:
Come possiamo osservare il risultato è uguale.
TERZA PROPRIETA’
La potenza di una potenza è una potenza che ha per base la
stessa base e per esponente il prodotto degli esponenti.
Quindi:
(am)n = a mn
POSITIVI.
- ponendo come condizione che m ed n siano NUMERI INTERI
Esempio:
(-32)3 = (9)3 = 729.
Ora proviamo ad applicare la regola precedente. Avremo:
Anche in questo caso il risultato è lo stesso.
QUARTA PROPRIETA’
Il prodotto tra due o più potenze aventi gli stessi esponenti è uguale ad una potenza che ha
per base il prodotto delle basi e per esponente lo stesso esponente.
Quindi:
am bm = (a b)m .
Esempio:
(-3)2 (+2)2 = (+9) (+4) = +36.
Ora proviamo ad applicare la regola precedente. Avremo:
Anche in questo caso il risultato è lo stesso.
QUINTA PROPRIETA’
Il quoziente tra due potenze aventi gli stessi esponenti è uguale ad una potenza che ha per
base il quoziente delle basi e per esponente lo stesso esponente.
Quindi:
am : bm = (a : b)m .
Esempio:
(-6)2 : (+2)2 = (+36) : (+4) = +9.
Ora proviamo ad applicare la regola precedente. Avremo:
Il risultato, come si può notare, è lo stesso.