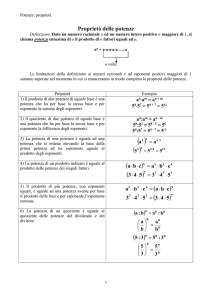
ALGEBRA
Esponenti
NOZIONI DI BASE
Moltiplicare un numero (Es. una misura) per se stesso significa ottenerne il quadrato, da cui m2.
Es: a . a = a 2
Moltiplicare un numero per se stesso tre volte significa ottenerne il cubo, da cui m3.
Es: a . a . a = a 3
In pratica, l’esponente indica quante volte un termine è moltiplicato per se stesso.
Quando in un’espressione compaiono dei termini a gradi differenti, non è possibile sommarli tra
loro, mentre nel prodotto o le frazioni, con alcune regole ben precise è possibile accorpare i termini.
Operazioni di moltiplicazione:
x2 x3 = x 2 + 3 = x 5
si sommano gli esponenti
Operazioni di divisione
x3 / x2 = x 3 - 2 = x1 = x
si sottraggono gli esponenti
Termini con lo stesso esponente:
x2 y2 = ( x y ) 2
,
( x / y ) 2 = x2 / y2
i termini ricevono l’esponente
Potenza di potenza
( x2 ) 3 = x
2x3
= x
6
si moltiplicano gli esponenti
Somme di termini uguali
x2 + x3 = x2 + x3
o, al massimo,
x2 + x2 = 2x2
Esponente nullo, negativo, fratto:
= x 1–1
x0 = 1
poiché
x0
x -1 = 1 / x
poiché
x2 / x3 = x 2 - 3 = x -1 = 1 / x
x 1/2 = x
0,5
= x/x = 1
ovvero x2 / x4 = x 2 - 4 = x-2 = 1 / x2
=
Date queste regole sinteticamente riportate è possibile compiere operazioni sulle espressioni di
diversi gradi, e interpretare meglio le operazioni con le radici.