Moltiplicazione

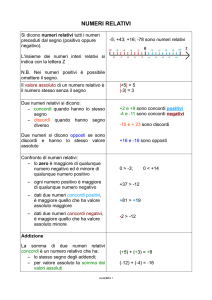
Moltiplicazione
Il prodotto di due numeri relativi è il numero relativo che ha per valore assoluto il
prodotto dei valori assoluti; il segno è positivo se i due numeri sono concordi,
negativo se sono discordi.
Es. :
(+5) (+8) = +40 ; (-6) (-7) = +42 ; (+9) (-4) = -36 ; (-3/4) (+3/5) = (-9/20)
Divisione
Il quoziente di due numeri relativi è il numero relativo che ha per valore assoluto il
quoziente del valore assoluto del divisore; è positivo se dividendo e divisore sono
concordi (stesso segno), è negativo se sono discordi (segno diverso).
Es.:
2 7
14
(+15):(+3)=(+5) ; (-20):(-5)=(+4) ; (+30):(-6)=(-5) ; (-2/5):(+3/7)=      
5
3
15
Elevamento a potenza
La potenza di un numero relativo è il prodotto di più fattori tutti uguali a quel
numero.
Il numero si chiama base; il numero dei fattori richiama esponente.
Es.:
 23   2 2 2   8
+2 = base
3 = esponente
La potenza di un numero relativo positivo è sempre positiva; la potenza di un numero
relativo negativo è positiva se l’esponente è pari, è negativa se l’esponente è dispari.
Es.:
 3
4
 81 ;
 4
3
 64 ;
 2
3
 8 ;
 2
3
4
8
 2
 16 ;     
27
 3