Classe 4A
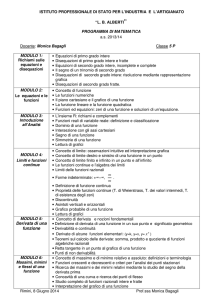
Programma di MATEMATICA
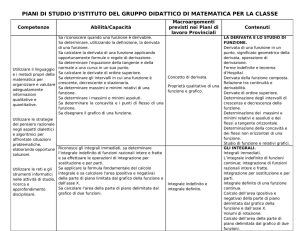
Modulo 1
Premesse all’analisi infinitesimale
Modulo 2
Limiti e continuità delle funzioni
Anno Scolastico 2014 - 2015
Prof.ssa Erminia Del Prete
La retta reale: insiemi numerici,
intervalli, intorni, insiemi limitati e
illimitati,
estremo
superiore
e
inferiore, punti di accumulazione,
punti isolati.
Funzioni:dominio,segno,intersezioni
con gli assi. Funzioni pari e dispari.
Condizioni di invertibilità di una
funzione.
Esempi con funzioni razionali intere e
fratte, logaritmiche ed esponenziali.
Disequazioni del tipo f(x)<o>k.
Limiti: concetto intuitivo di tutti i tipi
di limite (destro e sinistro, per difetto
e per eccesso),definizione generale di
limite. Verifica del limite finito o
infinito di una funzione per x che
tende a un valore finito o infinito.
Funzioni continue:definizione, punti
di discontinuità (le tre specie). Calcolo
dei limiti delle funzioni continue. Le
funzioni continue elementari. Regola
di De L’ Hôpital.
Modulo 3
L’algebra dei limiti e delle funzioni Teoremi sul calcolo dei limiti delle
continue
funzioni qualsiasi (senza dim.) e
conseguenze sul calcolo dei limiti delle
funzioni risultato di operazioni tra
funzioni continue. Forme
indeterminate. Limiti delle funzioni
polinomiali e delle funzioni razionali
fratte.
Modulo 4
Grafico probabile di una funzione
Costruzione del grafico probabile di
una funzione razionale intera o fratta
mediante rappresentazione grafica di:
dominio, segno della funzione,
intersezioni con gli assi, calcolo dei
limiti ai confini del dominio, eventuali
asintoti verticali, orizzontali,obliqui.
Modulo 5
Derivata di una funzione
Modulo 6
Studio di funzione
Derivate: definizione di rapporto
incrementale e di derivata di una
funzione in un punto. Significato
geometrico
del
valore
della
derivata di una funzione calcolato
in un punto del suo dominio.
Equazione della retta tangente al
grafico in un punto di ascissa xo. La
funzione derivata.
Punti
stazionari.
Interpretazione
geometrica di casi di non derivabilità:
flessi verticali, cuspidi, punti angolosi.
Continuità e derivabilità in un punto.
Derivate fondamentali. Teoremi sul
calcolo delle derivate (senza dim.),
tutte le regole di derivazione. Derivata
delle funzioni composte.
Segno della derivata prima: funzioni
crescenti
e
decrescenti.
Individuazione di max, min e flessi
orizzontali con lo studio del segno
della derivata prima.
Derivata seconda e concavità del
grafico,
ricerca dei flessi obliqui
mediante lo studio del segno della
derivata seconda.
Dall’equazione della funzione alla
traccia del suo grafico (aggiungendo
la ricerca di max, min, flessi e lo
studio della concavità alla costruzione
del grafico probabile).
Esercizi con funzioni razionali intere o
fratte
e
con
semplici
funzioni
esponenziali e logaritmiche.
Obiettivo minimo: sapere studiare l’andamento completo di una funzione
razionale fratta per costruirne il grafico.
Bologna, 6 giugno 2015
Gli alunni
L’ insegnante