ISTITUTO D’ISTRUZIONE SUPERIORE PROFESSIONALE E TECNICO COMMERCIALE
“A. CASAGRANDE” “F. CESI”
TERNI
A.S. 2015/2016
Disciplina
MATEMATICA
Docente
prof.ssa ROSA TIQUINO
Libri di testo usati “APPUNTI DI MATEMATICA” di Ilaria Fragni, Edizione Riforma,
Editore Cedam scuola (vol F)
PROGRAMMA SVOLTO NELLA CLASSE 5P
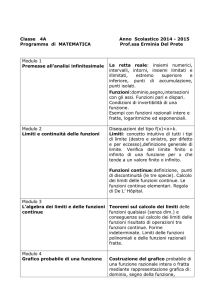
MODULO 1 Funzioni reali di variabile reale
-
Definizione di funzione in una variabile (dominio e codominio, classificazione)
Intervalli (definizione, limitati e illimitati, aperti, chiusi)
Determinazione del dominio di una funzione algebrica razionale e irrazionale, intera e fratta, e
della funzione esponenziale e logaritmica.
Definizione di grafico di una funzione e ricerca dei punti d’intersezione di una funzione con gli
assi cartesiani.
Determinazione degli intervalli di positività e di negatività di una funzione algebrica razionale
intera e fratta e loro rappresentazione grafica.
Definizione di funzione composta;
Lettura di grafici (dominio, codominio, segno, intersezione con gli assi)
MODULO 2 Limiti di funzioni reali di variabile reale e continuità
Unità 1
- Definizione di intorno di un punto
- Limite di una funzione (definizione a livello intuitivo, attraverso tabellina di valori)
- Limite destro e limite sinistro
- Limite finito ed infinito, per x tendente ad un valore finito c e per x tendente a più o meno
infinito;
- Riconoscimento del valore di un limite dal grafico
Unità 2
-
Definizione di funzione continua
Limite di funzioni continue
Algebra dei limiti
-
Forme indeterminate di funzioni razionali intere e fratte e loro risoluzione ( ,
Limite della funzione esponenziale e logaritmica attraverso la lettura del loro grafico.
Unità 3
0
0
,
)
-
Ricerca degli asintoti orizzontale e verticale per funzioni razionali e rappresentazione nel piano
cartesiano.
Ricerca dei punti di discontinuità (di prima, seconda e terza specie) per funzioni razionali.
MODULO 3 La derivata
Unità1
-
Derivata di una funzione in un punto (significato geometrico)
Derivata di alcune funzioni elementari
Algebra delle derivate
Unità 2
-
-
Funzioni crescenti e decrescenti (definizione)
Massimo e minimo assoluti e relativi (definizione)
Criterio per studiare, attraverso la derivata prima, la crescenza e la decrescenza di una funzione
razionale.
Significato geometrico del Teorema di Fermat (condizione necessaria per la ricerca di estremi
relativi)
Criterio per la ricerca di punti di massimo e di minimo relativi di una funzione razionale
attraverso la derivata prima.
Enunciato e applicazione del Teorema di De l’Hopital (per le forme indeterminate
funzioni razionali)
0
0
,
di
Unità 3
-
Definizione geometrica di funzione concava e convessa.
Definizione di flesso. Significato grafico di flesso a tangente orizzontale, verticale ed obliquo.
Criterio per stabilire la concavità e la convessità di una funzione razionale.
Criterio per la ricerca dei flessi attraverso la derivata seconda di una funzione razionale.
Unità 4
Studio di semplici funzioni razionali intere e fratte e rappresentazione probabile del grafico
FIRMA DEL DOCENTE __________________________________
FIRME ALUNNI p.p.v
1) __________________________
2) __________________________
3) _____________________________
DATA
_____________________