Le basi del calcolo statistico
equilibrio statistico di N particelle su k stati possibili:
•
descrizione del sistema: individuare gli stati possibili (microstati),
mediante i relativi numeri quantici
• calcolare l’energia Ei dell’i-esimo stato
• calcolare la degenerazione gi dell’i-esimo stato
• calcolare la probabilità di una certa partizione, cioè in quanti modi
si possono disporre Ni particelle sui k stati conservando l’energia totale a
disposizione (probabilità di una certa partizione di stati)
• ipotesi: tutti i microstati accessibili sono egualmente probabili
stat-1
4
4
4
4
4
4
4
4
4
4
4
4
4
4
4
4
3
3
3
3
3
3
3
2
2
2
2
2
1
1
1
0
+3
+2
+1
0
-1
-2
-3
+2
+1
0
-1
-2
+1
0
-1
0
3
3
3
3
3
3
3
3
3
2
2
2
2
2
1
1
1
0
+2
+1
0
-1
-2
+1
0
-1
0
2
2
2
2
1
1
1
0
+1
0
-1
0
1
1
0
0
gi
n
l
m
Microstati e macrostati
Esempio: microstati accessibili agli elettroni di atomi
di idrogeno per i primi 6 livelli energetici (macrostati)
pr2
L2
Ze 2
Hψ (r ,ϑ ,ϕ ) =
+
−
ψ ( r , ϑ , ϕ ) = Eψ ( r , ϑ , ϕ )
2m 2mr 2
r
m
ψ (r ,θ , ϕ ) = R(r )Yl l (ϑ ,ϕ ) =
u(r ) ml
Yl (ϑ , ϕ )
r
E6=-0,38
E5=-0,54
E4=-0,85
E3=-1,6
numeri quantici: ni, li,
livello energetico: Ei
mi
E2=-3,4
6
5
4
3
N6 36
N5 25
N4 16
N3 9
2
N2
4
degenerazione : gi
numero di occupazione: Ni
E1=-13,6
1
eV
i
N1
stat-2
Statistica di Boltzmann
Esempio:
probabilità della
Wi= numero di modi in cui si possono
partizione
disporre N i particelle sul livello i
N1=4
N2=3
N ( N − 1)(N − 2)(N − 3)
N!
W1 =
=
N3=5
N1!(N − N1)!
4!
N4=3
N5=4
( N − N1 )!
N2
g2
W2 =
N6=2
N 2 !( N − N1 − N 2 )!
N
gi i
W = N!Πi
N i!
si cerca il massimo di lnW con i vincoli
sul numero totale N di particelle e
l’energia totale E (massimo vincolato):
ln W = ln N !+
∑i N i = N
∑i N i Ei = E
E6=-0,38
E5=-0,54
E4=-0,85
E3=-1,6
E2=-3,4
4
4
4
4
4
4
4
4
4
4
4
4
4
4
4
4
3
3
3
3
3
3
3
2
2
2
2
2
1
1
1
0
+3
+2
+1
0
-1
-2
-3
+2
+1
0
-1
-2
+1
0
-1
0
3
3
3
3
3
3
3
3
3
2
2
2
2
2
1
1
1
0
+2
+1
0
-1
-2
+1
0
-1
0
2
2
2
2
1
1
1
0
+1
0
-1
0
1
1
0
0
gi
n
l
m
6
5
4
3
N6 36
N5 25
N4 16
N3 9
2
N2
4
∑i Ni ln gi − ∑i ln N i!
E1=-13,6
1
eV
i
stat-3
N1
Statistica di Boltzmann
metodo dei “moltiplicatori di Lagrange”
d ln Wi
dN i
dN i Ei
dNi = 0
−
−
α
β
∑i
dN i
dN i
dN i
si richiede che sia nullo ogni termine
della sommatoria
d ln Wi
1
= ln g i − (ln N i + N i
− 1)
dN i
Ni
ln g i − ln N i − α − βEi = 0 ;
N i = Cgi e
gi
fattore di
“spazio delle fasi”
− βEi
ln
formula di Stirling:
lnx! = x lnx - x
Ni
= −α − β E i
gi
β ha le dimensioni dell’inverso
di una energia β =1/ kBT
kB=costante di Boltzmann,
T=temperatura assoluta
fBol (E,T) = e-E/kT
funzione di distribuzione
di Boltzmann
Ni = Cgi f Bz ( E i , T )
stat-4
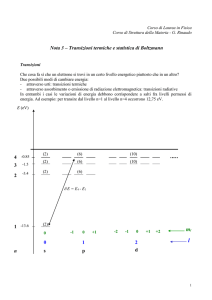
Esempio: distribuzione sui livelli energetici
di atomi di idrogeno a T=50000K
(temperatura di una stella?)
kBT = 8,6 ⋅10-5 eV K-1 ⋅5 ⋅ 104 K = 4,3 eV
i
gi
Ei
(eV)
fBlz(E i,T)
(e-E/kT )
gi f Blz
La distribuzione in energia di
elettroni di atomi di idrogeno
g fBlz
45
40
1
1
-13,6
24
24
2
4
-3,4
2,2
9
35
fBz
5 ⋅ 104 K
30
25
3
9
-1,6
1,5
13
4
16
-0,85
1,2
19
20
15
10
5
25
-0,54
1,14
28
6
36
-0,38
1,09
39
5
0
-16
-12
-8
-4
0
E (eV)
Per avere la probabilità di occupazione dello stato occorre
dividere per la funzione di partizione Z (“Zustand Summe”):
g f (E ,T )
Pi = i Bz i
Z
stat-5
La distribuzione in energia
di elettroni di atomi di idrogeno
a diverse temperature
25,00
ln(g fBlz)
6,5 ⋅ 103 K
20,00
15,00
T (K)
6500
10000
50000
kBT (eV)
fBz
10,00
0,55
0,85
4,25
5,00
scala logaritmica
0,00
-14
-10
-6
-2
E (eV)
25,00
25,00
ln(g fBlz)
ln(g fBlz)
5 ⋅ 104 K
20,00
15,00
15,00
10,00
10,00
fBz
fBz
5,00
5,00
0,00
0,00
-14
stat-6
104 K
20,00
-10
-6
E (eV)
-2
-14
-10
-6
E (eV)
-2