Presentazione di PowerPoint

Le basi del calcolo statistico
equilibrio statistico di N particelle su n stati possibili:
• descrizione del sistema: individuare gli stati possibili (microstati),
mediante i relativi numeri quantici
• calcolare l’energia Ei dell’i-esimo stato
• calcolare la degenerazione gi dell’i-esimo stato
• calcolare la probabilità di una certa partizione, cioè in quanti modi
si possono disporre Ni particelle sugli n stati conservando l’energia totale a
disposizione (probabilità di una certa partizione di stati)
• ipotesi: tutti i microstati accessibili sono egualmente probabili
Esempio: microstati accessibili a particelle di
massa m in una scatola cubica di lato L
1
( p x2  p 2y  p z2 ) ; H ( x, y, z )  E ( x, y, z )
2m
H
Microstati e macrostati
L
 ( x, y , z )  sen( k x x ) sen( k y y ) sen( k z z )
π
π
π
m x ; k y  m y ; kz  mz
L
L
L
1
1
2
2
3
3
2
3
1
3
1
2
3
2
3
1
2
1
6
6
E6
N6
5
E5
N5
2
2
2
1
4
E4
N4
1
1
3
1
3
1
3
1
1
3
3
E3
N3
1
2
2
2
1
2
2
2
1
3
2
E2
N2
1
1
2
1
2
1
2
1
1
3
livello energetico: Ei
1
E1
N1
1
1
1
degenerazione : gi
i
mz
gi
kx 
2 2
E
( k x  k 2y  k z2 )
2m
E
π 2 2
2
(
m
x
2
2mL
 m 2y
 mz2 )
E  Eo (mx2  m2y  mz2 )
numeri quantici: mx my
numero di occupazione: Ni
mz
1
mx my
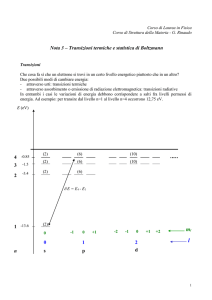
Livelli energetici
Esempio: un “gas” di elettroni in un cubo di lato 10-6 m
E o
π 2 (c) 2
2mc2 L2

10  (2 10 7 eVm ) 2
2  0,5 106 eV 1012 m 2
 4 10 7 eV
E1= Eo (1+1+1)=3Eo = 1,2  10-6 eV
E2= Eo (4+1+1)=6Eo = 2,4  10-6 eV
E3= Eo (4+4+1)=9Eo = 3,6  10-6 eV
E4= Eo (9+1+1)=11Eo = 4,4  10-6 eV
E5= Eo (4+4+4)=12Eo = 4,8  10-6 eV
E6= Eo (9+4+1)=14Eo = 5,6  10-6 eV
conteggio statistico secondo Boltzmann
Esempio:
probabilità della partizione
Wi= numero di modi in cui si possono
disporre Ni particelle sul livello i
N ( N  1)( N  2)( N  3)
N!
W1 

4!
N1! ( N  N1 )!
W2 
( N  N1 )!
N
g2 2
N 2!( N  N1  N 2 )!
N
gi i
W  N!  i
N i!
si cerca il massimo di lnW con i vincoli
sul numero totale N di particelle e
l’energia totale E (massimo vincolato):
ln W  ln N ! i Ni ln gi  i Ni !
i N i  N
i Ni Ei  E
N1=4
N2=3
N3=5
N4=3
N5=4
N6=2
1
1
2
2
3
3
2
3
3
1
1
2
3
2
1
3
2
1
6
6
E6
N6
5
E5
N5
2
2
2
1
4
E4
N4
1
1
3
1
3
1
3
1
1
3
3
E3
N3
1
2
2
2
1
2
2
2
1
3
2
E2
N2
1
1
2
1
2
1
2
1
1
3
1
E1
N1
1
1
1
mz
gi
i
1
mx my
metodo dei “moltiplicatori di Lagrange”
Statistica di Boltzmann
formula di Stirling:
lnx! = x lnx - x
 d ln Wi
dN
dNi Ei 
dNi  0
 i  
dN
dN
dN
i
i
i 

i 
d ln Wi
1
 ln g i (ln N i  N i
 1)
dN i
Ni
ln g i  ln N i    Ei  0 ; ln
N i  Cgi e
gi
fattore di
“spazio delle fasi”
Ni
   E i
gi
 Ei
 ha le dimensioni
dell’inverso di una energia
 =1/ kBT
fBol (E,T) = e-E/kT
funzione di distribuzione
di Boltzmann
Ni  Cgi f Bz ( E i , T )
g nel caso di distribuzione “continua” di energia,
con particelle di massa m
spazio delle fasi: caso
di particelle massive
energia cinetica: E=p2/2m
gi  g(E)
cella elementare dello spazio delle fasi:
dx dy dz dpx dpy dpz = h3
numero di celle elementari con energia fra E ed E+dE: occorre integrare
su tutte le variabili tranne il modulo di p che è legato all’energia E, quindi
esprimere d 3p in coordinate sferiche (d 3p = p2dp d  )
g ( E )dE 
p 2 dp
h
3
V 4
 dxdydz d 
g ( E )dE 
h
4V 2m3
h
per l’elettrone (due stati di spin):
3
3
2
p dp 
V 4 2m3
h
3
E dE
E dE
g ( E )dE 
8V 2m3
h
3
E dE
g ( E )dE 
8V 2m3
E dE
h3
py
pymax
in ciascuna
banda, E si
calcola a
partire dal
fondo della
banda e g(E) va
a zero alla cima
della banda
per p>pxmax lo spazio delle fasi
disponibile si riduce
progressivamente fino a
diventare un punto per p=pmax
pmax
E3max
g(E)
pxmax
px
E3min
terza banda
E2max
g(E)
3,5
3
E2min
Emax=10 eV
2,5
g(E)
spazio delle fasi nella
banda di energia
seconda banda
2
E1max
g(E)
E1min
1,5
1
0,5
0
0
2
4 E (eV) 6
8
10
prima banda
distribuzione
di Boltzmann
1.2
fBz
1
300 K
0.8
dNBz(E,T) =
g(E) fBz(E,T) dE
Se gli elettroni
seguissero la statistica
di Boltzmann:
la distribuzione attesa
sarebbe quella
mostrata in figura alle
due temperature
Da notare che la cima
della banda capita a
energie molto maggiori
delle energie termiche,
per cui non si vede
l’effetto della
diminuzione di g(E)
g
0.6
0.4
dNBz(E)/dE
0.2
0
0
20
40
60
80
100
80
100
E (meV)
1.2
fBz
1
100 K
0.8
g
0.6
0.4
dNBz (E)/dE
0.2
0
0
20
40
60
E (meV)
g nel caso di distribuzione “continua” di energia,
con particelle di massa nulla
energia: E = pc
spazio delle fasi: caso
di particelle di massa
nulla (fononi, fotoni)
cella elementare dello spazio delle fasi:
dx dy dz dpx dpy dpz = h3
numero di celle elementari con energia fra E ed E+dE: occorre integrare
su tutte le variabili tranne il modulo di p che è legato all’energia E, quindi
esprimere d 3p in coordinate sferiche (d 3p = p2dp d  )
g ( E )dE 
p 2 dp
h3
 dxdydz d 
per il fotone (due stati di polarizzazione):
per il fonone (due stati di
polarizzazione trasversale, uno di
polarizzazione longitudinale):
V 4
h3
2
p dp 
g ( E )dE 
V 4
(hc)3
V 8
(hc)3
E 2 dE
E 2dE
V 8  2 1  2
g ( E )dE 

E dE
3  3
3
h  vt vl 
distribuzione
di Boltzmann
dNBz(E,T) =
g(E) fBz(E,T) dE
120
fBz
100
300 K
80
g
60
Se i fotoni seguissero
la statistica di
Boltzmann
la distribuzione attesa
sarebbe quella
mostrata in figura
40
dNBz(E)/dE
20
0
0
50
100
150
energia (meV)
200
250
Statistiche quantistiche:
indistinguibilità classica e quantistica
z
x2, y2, z2,
px2, py2, pz2
x1, y1, z1,
px1, py1, pz1
y
x
z
m(x2, y2, z2 )
n(x1, y1, z1 )
y
indistinguibilità classica: le due particelle sono
identiche, lo stato in cui la particella “rossa” ha
coordinate (x1, y1, z1, px1, py1, pz1 ) e la particella
“verde” ha coordinate (x2, y2, z2, px2, py2, pz2 ) è
equivalente allo stato con le particelle scambiate
indistinguibilità quantistica: le due particelle sono
identiche, lo stato in cui la particella di coordinate (x1,
y1, z1) ha funzione d’onda n e la particella di
coordinate (x2, y2, z2) ha funzione d’onda m e lo stato
con le particelle scambiate vanno considerati entrambi
e sommati o sottratti a seconda del tipo di particella
 
Fermioni:  (r1,r 2 ) 
x
Bosoni:
1




( m (r1 ) n (r2 )   m (r2 ) n (r1 ))
2
1
 




 (r1,r 2) 
( m (r1 ) n (r2 )   m (r2 ) n (r1 ))
2
In quanti modi si possono disporre 2 particelle identiche in 3 celle?
Boltzmann
P
mx= 1
my= 1
mz= 2
a
b
a
b
Q
mx= 1
my= 2
mz= 1
b
a
ab
ab
Boltzmann:
R
mx= 2
my= 1
mz= 1
P
mx= 1
my= 1
mz= 2
Q
mx= 1
my= 2
mz= 1
Fermi
R
mx= 2
my= 1
mz= 1
P
mx= 1
my= 1
mz= 2
Q
mx= 1
my= 2
mz= 1
R
mx= 2
my= 1
mz= 1
b
a
b
a
a
b
per
Bose
ab
N
gi i
9

Ni !
2
indistinguibilità
classica e
quantistica
1
( P (a) Q (b)   P (b) Q (a))  1(a, b) 
2
1
 2 (a, b)  ( P (a) R (b)   P (b) R (a))  2 (a, b) 
2
1
 3 (a, b)  ( Q (a) R (b)   Q (b) R (a))  3 (a, b) 
2
 4 (a, b)   P (a) P (b)
 1 ( a, b) 
 5 (a, b)   Q (a) Q (b)
 6 (a, b)   R (a) R (b)
Bose:
6 modi
1
( P (a) Q (b)  P (b) Q (a))
2
1
( P (a) R (b)  P (b) R (a))
2
1
( Q (a) R (b)  Q (b) R (a))
2
Fermi:
3 modi
Statistica di
Bose - Einstein
Ni particelle in gi celle:
 in quanti modi si
possono mettere gi-1
“separatori” fra le Ni
particelle
P
mx= 1
my= 2
mz= 3
Q
mx= 1
my= 3
mz= 2
R
S
mx= 2
my= 1
mz= 3
mx= 2
my= 3
mz= 1
Ni    E / k T
i
B 1
e
nel continuo:
dN ( E )
 g ( E ) f BE ( E , T ) ;
dE
distribuzione di B.E.
U
mx=3
my= 1
mz= 2
tutte le possibili permutazioni di Ni+gi-1 oggetti
( N  g i 1)!
Wi  i
N i ! ( gi  1)!
 ln N i  ln( N i  g i 1)    Ei  0
N  gi
gi
ln i
   Ei ;
 1  e  Ei
Ni
Ni
gi
T
mx= 3
my= 2
mz= 1
;
g
N i    Ei
i 1
e
dN ( E )
g(E)
  E / k T
B 1
dE
e
1
f BE ( E , T )    E / k T
B 1
e
funzione di distribuzione di B.E.
Per i fotoni non c’è la conservazione
del numero totale   = 0
termine di spazio delle fasi per i fotoni:
due stati di polarizzazione
dN ( E )
g(E)
 E /k T
B 1
dE
e
8 V
g ( E )dE 
(hc)3
gas di
fotoni
E 2dE
120
300 K
100
distribuzione in energia:
dn( E )
8π
E2

dE
(hc)3 e E / k BT  1
dnBE
80
g
60
fBE
40
20
spettro di “corpo nero”
0
0
d ( )
8π
h 3

d
c 3 e h / k BT  1
50
100
150
energia (meV)
200
250
distribuzione in energia secondo Bose (Planck):
dn( E )
1
8πE 2
1
 g (E)

dE
e E / k BT  1 (hc)3 e E / k BT  1
confronto fra le
statistiche di Bose
e di Boltzmann
2
dn( E )
8
π
E

E
/
k
T
B 
secondo Boltzmann (Wien):
 g (E) e
e  E / k BT
dE
(hc)3
120
legge di Wien dello
“spostamento”
max T  3 103 mK
fBE
100
dnBz
80
dnBE
60
legge di Wien:
d ( )
  3e f ( / T )
d
g
40
fBz
20
0
legge di Rayleigh-Jeans
0
50
100
150
energia (meV)
200
250
confronto fra le
statistiche di Bose
e di Boltzmann
12000
secondo
Wien
10000
8000
spettro di
corpo nero
a 2000 K
6000
secondo
Planck
4000
2000
0
0
10
20
30
lambda (micron)
40
50
Statistica di
Fermi - Dirac
P
mx= 1
my= 2
mz= 3
Q
mx= 1
my= 3
mz= 2
R
mx= 2
my= 1
mz= 3
S
mx= 2
my= 3
mz= 1
mx= 3
my= 2
mz= 1
Ni particelle in gi celle:
 Ni “celle piene”,
 (gi-Ni ) “celle vuote”
g i ( gi  1)    ( gi  N i  1)
g i!
Wi 

Ni !
N i !( gi  N i )!
g i!
d ln W
ln W  i ln
;
   Ei  0
N i !( gi  N i )!
dN i
 ln N i  ln( gi  N i )    Ei  0
g  Ni
ln i
   Ei
Ni
;
gi
 1  e  Ei
Ni
Ni 
gi
gi
; Ni 
e  Ei  1
e( Ei  E F ) / k BT  1
T
U
mx=3
my= 1
mz= 2
Statistica di Fermi Dirac
elettroni in una banda non piena
g(E)
dN ( E )
g (E)

dE
e ( E  E F ) / k BT  1
fF(E,T)
T=0K
dN ( E )
 g ( E ) f F( E , T )
dE
1
f F( E , T )  ( E  E ) / k T
F
B 1
e
g(E)
fF(E,T)
T >> 0 K
 0,75
 0,5
 0,25
 kBT
l’integrale sull’energia di dN/dE è
pari al numero totale N di elettroni:

N
g ( E )dE
 e( E  E F ) / k BT  1

8V 2m3
h3
0
a T=0 K:

L’energia di Fermi
E dE
 e( E  E F ) / k B T  1
0
N
8π 2m3
n

V
h3
EF

E dE 
16π 2m3
0
h2  3n 
EF
 
8m  π 
3h3
3/ 2
EF
2/3
Esempio: il rame ha circa un elettrone libero per atomo, densità di circa 9
g/cm3 e numero di massa A=63
N mole g
6  1023 9 g 1023
1
n

 N Av A d 

3 mole g
3
3
63g cm
cm
cm
cm 3
N
4π 2 (c )2  3n 
EF
 
8mc2  π 
2/3

4  10  (2  105 eV  cm )2 3
8  0,5  106 eV
10  1045 cm  2  10eV
Energie di
Fermi
metallo
EF (eV)
TF (K)
Li
4,7
5,5104
Na
3,1
3,7104
TF = EF /kB
K
2,1
2,4104
kB 910-5eV K-1
Cu
7,0
8,2104
Ag
5,5
6,4104
Au
5,5
6,4104
TF >> T ambiente
EF >> energia termica a
temperatura ambiente
il gas di elettroni non è in
equilibrio energetico con il
reticolo
tipica energia
termica a
temperatura
ambiente
Energia media
<E>
Energia media a 0 K:
EF
C
E
3/ 2
dE
2 5/ 2
EF
3
5
0
 ET  0K  E

 EF
2 3/ 2
F
5
EF
1/ 2
C E
dE
3

0
<E> aumenta di poco per eccitazione
termica al crescere della temperatura:
solo una frazione di elettroni dell’ordine
di kBT/EF  qualche percento intorno al
livello di Fermi può acquistare energia
passando a livelli di energia >EF
<E>  kBT (kBT/EF )  (kBT)2 /EF
T >> 0 K
 kBT
Tutte le variazioni di stato interessano solo la fascia di elettroni intorno e EF
Gli elettroni molto distanti da EF sono “congelati” nel loro stato