ISTIT UTO DI ISTRUZIONE SUPERIORE
“CARLO UBERTINI”
Sede legale: Piazza Mazzini, 4 – 10014 CALUSO (TO)
e-mail: [email protected] - PEC: [email protected]
IST. PROF. SERVIZI PER L’AGRICOLTURA E LO SVILUPPO RURALE CON CONVITTO ANNESSO
IST. PROF. SERVIZI PER L’ENOGASTRONOMIA E L’OSPITALITÀ ALBERGHIERA
IST. PROF. SERVIZI PER L’ENOGASTRONOMIA E L’OSPITALITÀ ALBERGHIERA
10014 CALUSO
10014 CALUSO
10034 CHIVASSO
011.9833142
011.9833350
011.9175712
Piano n. 023 Rev. 3 del 22.10.2016
Documento
PIANO DI LAVORO ANNUALE
Anno Scolastico 2016 – 2017
Indirizzo Servizi per l’agricoltura e lo sviluppo rurale
Disciplina MATEMATICA
Docente titolare Prof.ssa Lara DEMARIA
Data 11–11–2016
Sede
Classe
Ore settimanali
Caluso
3C
3
Libro di testo "MultiMath.giallo - Vol.3" di P. Baroncini e R. Manfredi; Ed. Ghisetti & Corvi
1.
PROFILO INIZIALE DELLA CLASSE
Si rimanda alle indicazioni emerse durante i Consigli di Classe.
2.
FINALITA’ GENERALI DELLA DISCIPLINA
3.
utilizzare il linguaggio e i metodi propri della matematica per organizzare e valutare adeguatamente
informazioni qualitative e quantitative
rendere autonomi gli studenti nell’utilizzo del linguaggio e dei formalismi tipici della disciplina
migliorare la loro capacità di analisi e di rielaborazione
acquisire abilità necessarie per applicare i principi e i processi matematici di base nel contesto quotidiano
possedere gli strumenti matematici necessari per la comprensione delle discipline professionalizzanti
concorrere alla costituzione di un bagaglio di competenze spendibili in ambito lavorativo e professionale
METODI E STRUMENTI DIDATTICI
Le modalità di lavoro che si intendono utilizzare sono:
lezione frontale
lezione interattiva
esercitazioni individuali o a piccoli gruppi guidate dal docente
problem solving
lavoro di gruppo
attività di laboratorio
attività di recupero/sostegno
pl-Demaria-3C-matematica
Pagina 1 di 4
Gli strumenti di lavoro che si intendono utilizzare sono:
4.
libro di testo
dispense o fotocopie (eventualmente)
quaderno
lavagna
laboratorio
CRITERI DI VALUTAZIONE E VERIFICA
Nel corso di ciascun periodo didattico, verranno effettuate almeno tre prove scritte e una prova orale (utilizzando
l’interrogazione orale o effettuando una prova scritta valevole per l’orale). Per le prove scritte, verranno utilizzate le seguenti
tipologie:
Quesito vero/falso
Domande a scelta multipla
Esercizi da risolvere
Problemi da risolvere
Grafici da realizzare e/o interpretare
Per quanto riguarda la valutazione, si fa riferimento alla “Griglia di descrizione del significato dei voti” deliberata dal Collegio
dei Docenti e allegata al PTOF.
5.
MODALITA’ DI RECUPERO.
Ogni qualvolta l’accertamento delle competenze rileverà lacune, il recupero sarà realizzato con le seguenti modalità:
“in itinere” quando si riterrà opportuno svolgere lezioni di rinforzo per l’intero gruppo classe, con particolare
attenzione agli studenti che abbiano evidenziato carenze negli apprendimenti, assegnando se necessario anche un
lavoro supplementare da svolgere autonomamente;
e-learning, con l’ausilio della piattaforma MOODLE
lavoro di gruppo
pausa didattica, nel caso si assegnino attività differenziate a gruppi di allievi (approfondimento per alcuni e recupero
per altri) senza procedere con le attività programmate
IDEI, ossia interventi didattici educativi integrati, riservati agli studenti con difficoltà, al di fuori dell’orario
curriculare
attività di sportello didattico
pl-Demaria-3C-matematica
Pagina 2 di 4
6.
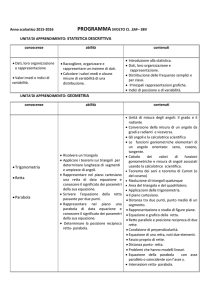
CONTENUTI DEL PROGRAMMA E TEMPI, ARTICOLAZIONE DELLE COMPETENZE IN ABILITA’ E
CONOSCENZE.
TEMPI di
svolgimento
COMPETENZE DI BASE
ABILITA’/CAPACITA’
Utilizzare consapevolmente le
procedure e le tecniche del calcolo
algebrico.
Saper risolvere equazioni di primo
e secondo grado, sistemi lineari di
due equazioni in due incognite.
Richiami di algebra: equazioni di
secondo grado, sistemi di
equazioni e radicali.
Settembre
Saper determinare il punto medio
di un segmento e la lunghezza del
segmento stesso.
Saper individuare un punto su un
asse conoscendone la distanza da
un altro punto.
Conoscendo il punto medio e un
estremo di un segmento
individuare l’altro estremo.
Perimetro e area di figure
geometriche nel piano cartesiano.
Il piano cartesiano. Le coordinate
cartesiane dei punti. La
corrispondenza biunivoca tra punti
del piano e coppie ordinate di
numeri.
Distanza tra due punti. Punto
medio di un segmento.
Ottobre,
novembre
Tracciare il grafico di una retta
conoscendone l'equazione.
Determinare l'equazione di una
retta per un punto, noto il
coefficiente angolare.
Determinare l'equazione di una
retta passante per due punti.
Stabilire la mutua posizione di due
rette nel piano.
Determinare le coordinate del
punto di intersezione fra due rette.
Calcolare la distanza di un punto
da una retta.
Determinare l'equazione dell'asse
di un segmento.
Equazione della retta parallela agli
assi, passante per l'origine e in
posizione generica.
Equazione della retta in forma
implicita ed esplicita.
Condizione di appartenenza di un
punto ad una retta.
Significato
geometrico
del
coefficiente angolare e del termine
noto.
Relazioni di parallelismo e di
perpendicolarità tra rette e come si
traducono in relazioni tra i loro
coefficienti angolari.
Novembre,
dicembre
Determinare l'equazione di una
circonferenza noto il centro e il
raggio.
Stabilire quando un'equazione di
secondo grado in x e in y
rappresenta una circonferenza.
Rappresentare graficamente una
circonferenza,
nota
la
sua
equazione.
Determinare le coordinate del
centro e la misura del raggio nota
l'equazione
canonica
della
circonferenza.
Determinare le coordinate dei
punti di intersezione di una retta e
di una circonferenza.
La circonferenza come luogo
geometrico.
Equazione di una circonferenza.
Le relazioni tra i coefficienti
dell'equazione della circonferenza
e le coordinate del centro e la
misura del raggio.
Posizioni reciproche di una retta e
di una circonferenza.
Dicembre,
gennaio
Trasformare una relazione
geometrica tra punti del piano in
una relazione algebrica tra le loro
coordinate.
Utilizzare le strategie appropriate
per risolvere problemi di
geometrica analitica.
pl-Demaria-3C-matematica
CONOSCENZE
Pagina 3 di 4
Padroneggiare calcoli con angoli
espressi sia nel sistema
sessadecimale sia in radianti.
Comprendere il significato delle
funzioni goniometriche e
utilizzarle anche graficamente.
Utilizzare le formule
goniometriche nella risoluzione di
problemi.
Saper individuare stategie
trigonometriche opportune per
risolvere problemi di varia natura.
Trasformare una relazione
geometrica tra punti del piano in
una relazione algebrica tra le loro
coordinate.
Utilizzare le strategie appropriate
per risolvere problemi di
geometrica analitica.
Utilizzare consapevolmente le
procedure e le tecniche del calcolo
algebrico.
Convertire la misura di un angolo
da un sistema di misura all'altro.
Rappresentare graficamente le tre
funzioni fondamentali.
Utilizzare le relazioni tra le
funzioni goniometriche al fine di
calcolare il valore di semplici
espressioni.
Comprendere e saper utilizzare le
relazioni
fra
le
funzioni
goniometriche di angoli associati
al fine di calcolare il valore di
semplici espressioni.
Risolvere equazioni goniometriche
di
risoluzione
immediata,
utilizzando anche la calcolatrice
scientifica.
I sistemi di misura degli angoli.
La circonferenza goniometrica.
Funzioni goniometriche di un
angolo: seno, coseno e tangente.
Rappresentazione grafica della
variazione di seno, coseno e
tangente.
Relazioni fondamentali tra le varie
funzioni goniometriche.
Funzioni goniometriche di angoli
notevoli ( 45°, 30°, 60° )
Angoli associati.
Equazioni
goniometriche
elementari e a esse riconducibili.
Risolvere i triangoli rettangoli.
Determinare l'area di un triangolo
noti due lati e l'angolo compreso.
Risolvere i triangoli qualsiasi.
Risolvere
semplici
problemi
relativi alle misure dei lati e degli
angoli di un triangolo rettangolo e
di un triangolo qualsiasi.
Definizioni relative ai triangoli
(catalogazione, altezze, mediane,
bisettrici)
Relazioni tra i lati e gli angoli di
un triangolo rettangolo.
Relazioni tra i lati e gli angoli di
un triangolo qualsiasi: teorema del
Seno e il teorema di Carnot.
Interpretare i coefficienti
dell'equazione della parabola allo
scopo di individuarne le varie
caratteristiche e la posizione nel
piano.
Individuare le coordinate dei punti
di intersezione fra una parabola e
gli assi cartesiani.
Tracciare il grafico di una
parabola di cui è nota l'equazione.
Determinare vertice, fuoco e
direttrice di una parabola di data
equazione.
Determinare le coordinate dei
punti di intersezione rettaparabola.
Scrivere l'equazione di una
parabola soddisfacente a date
condizioni.
La definizione di parabola come
luogo geometrico.
Equazione della parabola come
grafico della funzione di secondo
grado.
Posizione di una parabola rispetto
agli assi cartesiani.
Equazione della parabola con asse
di simmetria parallelo all'asse y.
Coordinate del fuoco, del vertice;
equazione della direttrice.
Le relazioni tra i coefficienti della
parabola e i suoi elementi.
Equazione della parabola passante
per tre punti.
Risoluzione algebrica e grafica di
equazioni e disequazioni di
secondo grado
Disequazioni di secondo grado
intere e frazionarie.
Sistemi di disequazioni di secondo
grado.
Gennaio,
febbraio,
marzo
Marzo,
aprile
Aprile,
maggio
Maggio,
giugno
Firma
Prof.ssa Lara DEMARIA
pl-Demaria-3C-matematica
Pagina 4 di 4