author: Ing, Giulio De Meo
GEOMETRIA
TEOREMI FONDAMENTALI DI GEOMETRIA
GEOMETRIA ELEMENTARE
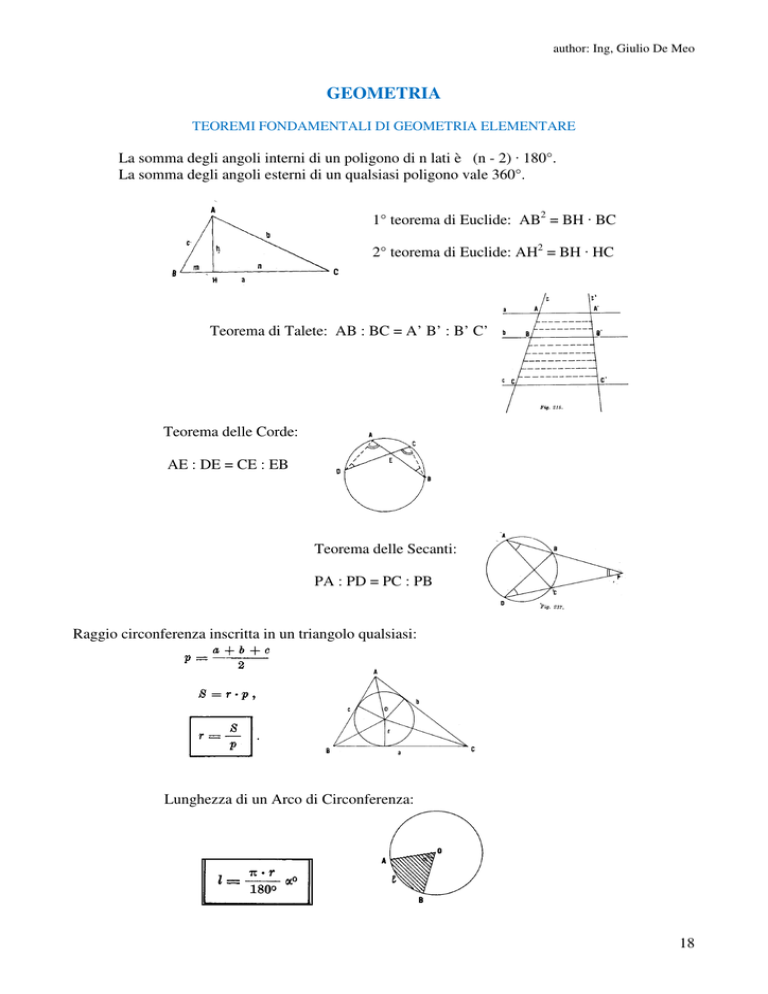
La somma degli angoli interni di un poligono di n lati è (n - 2) · 180°.
La somma degli angoli esterni di un qualsiasi poligono vale 360°.
1° teorema di Euclide: AB2 = BH · BC
2° teorema di Euclide: AH2 = BH · HC
Teorema di Talete: AB : BC = A’ B’ : B’ C’
Teorema delle Corde:
AE : DE = CE : EB
Teorema delle Secanti:
PA : PD = PC : PB
Raggio circonferenza inscritta in un triangolo qualsiasi:
Lunghezza di un Arco di Circonferenza:
Cir
18
author: Ing, Giulio De Meo
AREA DI FIGURE PIANE
A = b ·h
Parallelogrammo:
h
b
b
Trapezio: A = ( B + b ) · h
2
h
A
B
Rombo:
A = D · d = ( A B · CD )
2
2
C
D
B
Triangolo: l’area di un triangolo qualsiasi di cui si conosce la misura dei tre lati si può
determinare con la Formula di Erone:
semiperimetro p = a + b + c
2
Area =
p ( p - a ) ( p - b) ( p - c)
a
b
h
c
= ½ (c· h)
Risoluzione di un Triangolo Rettangolo:
A
Se di un triangolo rettangolo si conosce la relazione tra 2 lati o
tra 2 angoli, si può risolvere utilizzando i teoremi di Pitagora
3x
h
e di Euclide e la proporzione nell’incognita x.
esempio:
C
se AC = ¾ AB e la loro somma è 49cm per risolvere
basta porre : AC= 3x; AB= 4x; quindi AC+AB= 7x = 49cm;
allora x=7cm; AC = 3x =21cm; AB = 4x = 28cm;
Area= ½ AC AB = 294cm2 ;
4x
B
Poligono Regolare: A= prodotto del Semiperimetro p moltiplicato l’apotema :
p= P
2
a
Quadrato:
A= p·a
Area = lato 2 ; Diagonale = lato · √ 2 ;
19
author: Ing, Giulio De Meo
GEOMETRIA PIANA
Distanza tra 2 punti A ( x1 , y1 ) e B ( x2 , y2 ) :
AB = √ (x2 – x1 )2 + (y2 – y1 )2
x1 + x2 y1 + y2
,
.
2
2
Punto medio: M
Eq. implicita di una retta:
Eq. esplicita retta: y = mx + q ;
ax + by + c =0 ;
m= – a/b; q = – c/b;
Coeff angolare retta passante per 2 punti: m = (y2 – y1 ) / ( x2 – x1 ) ;
Eq retta di coefficiente angolare ‘m’ e passante per un punto P(x0,y0)
y − y0 = m ( x − x0 )
Anche eq. fascio proprio di rette di centro (x0 , y0 ):
Retta passante per due punti A(x1,y1) , B(x2,y2):
Distanza di un punto P(x0,y0) da una retta: d =
y − y1
x − x1
=
y2 − y1 x2 − x1
ax0 + by0 + c
a2 + b2
.
Luoghi Geometrici: equazione della bisettrice di due rette:
ax + by + c
=
± a1x + b1 y+ c1
√ ( a2 + b2 )
Quesiti su un Triangolo di vertici
√ ( a12 + b12 )
A(x1,y1) , B(x2,y2) C(x3,y3)
Coordinate del Baricentro del triangolo :
Area del Triangolo noti i vertici (regola di Sarrus):
20
author: Ing, Giulio De Meo
Punti Notevoli di un TRIANGOLO
Altezza: segmento congiungente un vertice ed il
suo lato opposto che incide perpendicolarmente
(cioè forma un angolo di 90°);
90°)
Ortocentro: punto di incontro delle Altezze.
Mediana: segmento congiungente un vertice ed il
punto medio del lato opposto.
Baricentro: punto di incontro delle mediane;
inoltre si ha:
AG = 2 GMa ;
BG = 2 Mb ;
CG = 2 Mc ;
Bisettrice: retta congiungente un lato ed il vertice
opposto che divide il suo angolo in 2 angoli uguali.
Incentro: punto di incontro delle Bisettrici,
coincidente con il centro della circonferenza
inscritta nel triangolo.
Asse: segmento perpendicolare ad un lato e
passante per il suo punto medio M
Circocentro: punto di incontro degli assi
coincidente con il centro della circonferenza
circoscritta al triangolo.
21
author: Ing, Giulio De Meo
CONICHE
Una conica è una curva ottenuta dalla intersezione di un cono circolare retto con un piano.
Analizziamo alcuni tipi di coniche reali: Circonferenza, Ellisse, Parabola ed Iperbole.
Circonferenza
La circonferenza è il luogo dei punti del piano equidistanti da un punto fisso detto centro.
( x – α )2 + ( y – β )2 = r 2
x 2 + y 2 + ax + by + c = 0 .
centro: C ( α , β ) ; a = - 2α ;
Lunghezza del raggio: r =
c = α2 + β2 – r2
b = -2β ;
a2 + b2
4
-c
Ellisse
L’ellisse è il luogo geometrico dei punti del piano per i quali è costante la somma
delle distanze da due punti fissi detti fuochi.
Consideriamo dapprima il caso di un ellisse con Fuochi sull’asse X centrato in O:
a>b:
b
x2 y2
+
=1
a2 b2
-a
F2
F1
a
F1 ( - c , 0 ) ;
F2 ( c , 0 ) ;
b
c2 = a 2 − b2
Eccentricità : e =
c
<1
a
Consideriamo adesso il caso di un ellisse con Fuochi sull’asse Y centrato in O:
b
a<b:
F1 ( 0, - c ) ;
c 2 = b2 ─ a2 ;
F2
-a
=
F2 ( 0 , c) ;
<1
a
F1
-b
Nel caso in cui l’ellisse sia centrato in un punto P( xo,yo) diverso dall’origine, la sua
equazione è
( x ─ xo ) 2 + ( y ─ yo ) 2 = 1
a2
b2
22
author: Ing, Giulio De Meo
Parabola
La parabola è il luogo dei punti del piano equidistanti da un punto fisso detto fuoco e da una
retta fissa detta direttrice.
Una parabola con asse di simmetria parallelo all’asse Y ha equazione:
y = ax 2 + bx + c
Vertice :
V ( - b/2a , -∆/4a )
∆
1
b
,−
+
.
2a 4a 4a
fuoco: F −
se a > 0 concavità verso l’alto
eq. asse di simmetria: X = -b/2a ;
Eq. direttrice: y = −
∆
1
.
−
4a 4a
se a < 0 concavità verso il basso
Una PARABOLA con asse di simmetria parallelo all’asse X ha equazione:
x = ay 2 + by + c
Fuoco :
1
b
∆
F −
+ ,−
4 a 4a 2 a
Vertice: V ( -∆/4a , -b/2a )
se a > 0 concavità verso destra
eq. asse di simmetria: Y = -b/2a ;
eq direttrice : x = - (1+∆) / 4a ;
se a < 0 concavità verso sinistra
23
author: Ing, Giulio De Meo
Iperbole
L’iperbole è il luogo geometrico dei punti del piano per i quali è costante (in valore assoluto)
la differenza delle distanze da due punti fissi detti fuochi.
Consideriamo dapprima il caso di un’iperbole con Fuochi sull’asse X centrata in O:
x2 y 2
−
=1 ;
a 2 b2
eccentricità:
b
F1
-a
c 2 = a 2 + b2 ;
a
e=
Asintoti dell’iperbole:
F2
-b
1
c
>1
a
y=−
F ( ± c , 0 );
b
b
x; y= x;
a
a
Coeff angolare tangente alla
iperbole nel punto di ascissa
xo
Equaz tangente nel punto
P (Xo, Yo)
Nel caso in cui l’iperbole ha fuochi sull’asse Y o anche, interseca l’asse Y:
y2
x2
–– – –– = – 1 ;
a2
b2
c2 = a2 + b2 ;
c
e = –– > 1 ;
b
F ( 0 , ± c );
Asintoti dell’iperbole:
y=−
b
b
x; y= x
a
a
24
author: Ing, Giulio De Meo
Iperbole Equilatera:
Un’iperbole si dice equilatera quando i suoi asintoti sono perpendicolari tra loro. ( a = b ) :
x2 − y 2 = a2
oppure
eccentricità: √2 ; 2
2 Asintoti:
y=x ;
y = −x ;
fuochi F ( ± c , 0 ) ;
Se gli asintoti corrispondono agli assi allora l’equazione generale dell’iperbole diventa:
xy = k ; in particolare, se k > 0 l’iperbole è nel 1° e 3° quadrante, se
se k < 0 nel 2° e 4°.
Iperbole Equilatera riferita agli asintoti: xy = k con
Vertici:
V
> 0 ; = √2 √
,
√
V
√
,
√
Fuochi:
√2 , √2 ; √2 , √2
Funzione OMOGRAFICA :
y = ax + b
con a,b,c,d costanti reali.
cx + d
se c=0 oppure se c≠00 e ad = bc la funzione è una retta.
se c≠0 e ad ≠ bc la funzione è un’ Iperbole Equilatera Traslata con asintoti x = -d/c ; y = a/c
che sono le coordinate del nuovo centro O’ dell’
dell iperbole equilatera traslata.
raslata.
Operando la traslazione d’assi sotto si ottiene una
iperbole equilatera del tipo xy = k ;
25
author: Ing, Giulio De Meo
CLASSIFICAZIONE E RIDUZIONE DI UNA CONICA
Analiticamente una conica è espressa da un’equazione del 2° ordine a coefficienti reali:
f(x,y) = a11 x2 + a22 y2 + 2 a12 x y + 2 a13 x + 2 a23 y + a33=0
ed in coordinate omogenee :
f(x1,x2,x3) = a11 x12 + a22 x22 + a33 x32 + 2 a12 x1 x 2 + 2 a13 x1 x 3 +2 a23 x2 x 3 = 0
ad essa si associa la matrice A: se Det(A) = 0 la conica si dice DEGENERE o RIDUCIBILE.
Si può classificare la conica in base al complemento algebrico A33 della matrice:
A33 = a11 a22 – ( a12 ) 2
si hanno 3 casi:
-
A=
A33 > 0 : la conica è un’ Ellisse;
A33 = 0 : la conica è una Parabola;
A33 < 0 : la conica è un’ Iperbole.
a 11
a 12
a 13
a 12
a 22
a 23
a 13
a 23
a 33
RIDUZIONE A FORMA CANONICA
L’equazione completa della conica si può semplificare passando ad una forma ridotta detta canonica: basta
calcolare il determinante Det(A), il valore di A33 e la somma I = a11 + a22 . Quindi si hanno 2 casi:
a x12 + b x22 + c x32 = 0;
1) coniche a centro (Ellisse o Iperboli) : equazione ridotta
i coefficienti a, b, c si determinano
risolvendo il sistema
2) Parabola:
i coefficienti a e b si determinano
risolvendo il sistema
A33 · c = det ( A )
a+b = I
a · b = A33
a x12 + 2 b x2 x3 = 0;
equazione ridotta
a =
I
- a · ( b )2 = det(A)
26
author: Ing, Giulio De Meo
CLASSIFICAZIONE AFFINE DELLE QUADRICHE
La quadrica
Q : XT A X
di equazione:
a11 x2 + a22 y2 + a33 z2 + 2 a12 x y + 2 a13 x z + 2 a23 y z + 2 a14 x + 2 a24 y + 2 a34 z + a44=0
a11 x12 + a22 x22 + a33 x32 + a44 x42 + 2 a12 x1 x 2 + 2 a13 x1 x 3 +2 a23 x2 x 3 +2 a14 x1 x 4 +
+ 2 a24 x2 x 4 = 0
e di matrice simmetrica
a 11
a 12
a 13
a 14
a 12
a 22
a 23
a 24
a 13
a 23
a 33
a 34
a 14
a 24
a 34
a 44
A=
si può classificare in base al DET (A) , al valore di A 44 ed alla Conica impropria C∞ sezione della quadrica
con il piano improprio X4 = 0 .
La conica C∞ si determina dalla equazione Q della quadrica eliminanando i termini di X, Y, Z e noto.
C∞ è riducibile se il determinante della sua matrice è nullo;
C∞ è reale se il discriminante della sua equaz. ∆ ≥ 0 ; è detta immaginaria nel caso contrario.
1) DET(A) ≠ 0 - QUADRICA GENERALE: (Ellissoide, Paraboloide o Iperboloide):
det(A) > 0 Ellissoide Immaginario
det(A) < 0 Ellissoide Reale a punti ellittici
● se A44 ≠ 0 e C∞ = immaginaria
● se A44 ≠ 0 e C∞ = reale non degenere
● se A44 = 0 e C∞ = degenere
2)
det(A) > 0 Iperboloide ad 1 falda a punti Iperbolici
det(A) < 0 Iperboloide a 2 falde e punti Ellittici
det(A) > 0 Paraboloide iperbolico a sella a punti iperbolici
det(A) < 0 Paraboloide ellittico a punti ellittici
DET(A) = 0 QUADRICA SPECIALIZZATA : (Cilindro o Cono):
□ se Det (A) = 0 e Rango (A) = 3
● se A44 ≠ 0 e C∞ = immaginaria :
● se A44 ≠ 0 e C∞ = reale non degenere:
● se A44 = 0 e C∞ = riducibile in
Cono Immaginario;
Cono Reale
2 rette reali e distinte:
Cilindro Iperbolico
2 rette reali e coincidenti:
2 rette complesse coniugate:
Cilindro Parabolico
Cilindro Ellittico
□ se Det (A) = 0 e Rango (A) < 3
● se Rango(A) = 2 - Quadrica riducibile composta da 2 Piani distinti:
● se Rango(A) = 1 - Quadrica riducibile composta da 2 Piani coincidenti:
27
author: Ing, Giulio De Meo
FASCI DI RETTE
Fascio Proprio: insieme di tutte le rette del piano che passano per un punto comune detto Centro.
Se il centro è C (x0 , y0 ) l’eq del fascio è:
y - y0 = m ( x - x0 ) che equivale all’equazione
(ax + by + c) + k (a1 x + b1 y + c1 ) = 0 ;
(*)
le due rette entro parentesi sono le generatrici del fascio.
Se si conosce l’eq del fascio, per ricavarne il Centro basta fare
Sistema tra 2 qualsiasi rette del fascio. Se si conoscono 2 rette,
basta scrivererle nella forma (*) per determinare il fascio.
Dato il fascio, la retta passante per un punto dato la si determina sostituendo le coordinate del punto
nell’ equazione del fascio (*).
Fascio Improprio: ax + by + k = 0
insieme delle rette del piano parallele ad una retta data.
FASCI DI CIRCONFERENZE
Sia data l’equazione del fascio generico come combinazione lineare di 2 circonferenze:
( x2 + y2 + a1 x + b1 y + c1 ) + k ( x2 + y2 + a2 x + b2 y + c2 ) = 0 ;
(*)
Si determina il Centro del fascio portando l’equazione del fascio in forma implicita:
x2 + y2 + ax + by + c = 0 ;
o facendo sistema tra le equazioni delle 2 circonf. date.
Distinguiamo 4 tipi di Fascio:
1) Fascio di circoli Secanti:
Tutte le circonferenze si intersecano in 2 punti A e B (punti base)
La retta AB è detta asse radicale
(circonf. degenere di raggio ∞ ).
L’asse del segmento AB su gui giacciono i centri delle
circonferenze è detto asse centrale.
2) Fascio di circoli Tangenti:
Tutte le circonferenze sono tra loro tangenti in un solo punto T
L’asse radicale è la retta r passante per T (x0 , y0 )
l’equaz del fascio si può scrivere come c.l. dell’equazione
della retta r:
[ ( x – x0 )2 + ( y – y0 )2 ] + k (ax + by + c) = 0
T
3) Fascio di circoli concentrici:
x2 + y2 + ax + by + k = 0
tutte I circoli sono concentrici.
28












