Modellistica Chimica e Catalisi

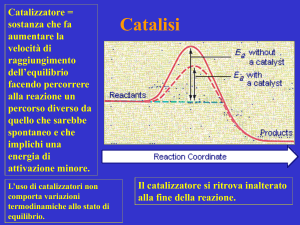
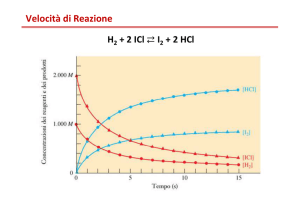
Chimica Computazionale e Catalisi
Catalisi
Modellistica Chimica e Catalisi
Dario Duca
Dipartimento di Fisica e Chimica dell’Università di Palermo
Chimica Metallorganica e Catalisi, A.A. 2016 – 2017
Chimica Metallorganica e Catalisi
Dipartimento di Fisica e Chimica dell’Università di Palermo
Chimica Computazionale e Catalisi
Indice
Chimica Computazionale e Catalisi
Modellistica Chimica in Catalisi
Metodi Modellistici
Catalysis: Concepts and Green Applications
Lecture slides for Chapter 6: Computer
applications in catalysis research.
Most of the graphics here were drawn using
PowerPoint and Chemdraw (version Ultra 9.0).
Feel free to modify and/or add your own
pyrotechnics.
Please send any feedback to
[email protected]
Catalysis/ Rothenberg, ISBN 978-3-527-31824-7.
Chimica Metallorganica e Catalisi
www.catalysisbook.org
Dipartimento di Fisica e Chimica dell’Università di Palermo
Chimica Computazionale e Catalisi
Modellistica Chimica in Catalisi
Indice
Chimica Computazionale e Catalisi
Modellistica Chimica in Catalisi
Metodi Modellistici
Chimica Metallorganica e Catalisi
Dipartimento di Fisica e Chimica dell’Università di Palermo
Chimica Computazionale e Catalisi
Modellistica Chimica in Catalisi
Figure 6.1
Computational
Green Chemistry
I gli “esperimenti” computazionali nelle applicazioni catalitiche possono essere
schematizzate con il seguente diagramma a blocchi:
catalyst
design
catalytic
cycles
(catalytic
processes)
QSAR/ QSPR
Reaction kinetics
ab initio, DFT
3D
descriptors
active
intermediates
semi-empirical
methods
2D
descriptors
mechanistic
studies
empirical
scales
activation/
deactivation
Classical
mechanics
Quantum
mechanics
molecular
dynamics
Monte-Carlo
methods
QM/MM
hybrid methods
I sebbene inquadrabili fra gli approcci computazionali non ci si occuperà
dell’ottimizzazione reattoristica e di processo
Chimica Metallorganica e Catalisi
Dipartimento di Fisica e Chimica dell’Università di Palermo
Chimica Computazionale e Catalisi
Modellistica Chimica in Catalisi
Computational Green Chemistry
I fra i vantaggi dell’approccio teorico bisogna annoverare il fatto che in un
esperimento computazionale possono essere simulate condizioni estreme od
anche “inesistenti” (nelle proprietà del processo o del reattore);
I un altro vantaggio è rappresentato dalla possibilità di simulare specie intermedie
(ad es. specie semi-idrogenate) o stati di transizione che non possono essere
isolate sperimentalmente;
I la possibilità di matematizzare e riprodurre modellisticamente le nostre idee è
infine il più importante fra i vantaggi nell’utilizzo dell’approccio computazionale;
I un ulteriore utilizzo dell’approccio computazionale riguarda l’analisi dei dati e il
data mining attraverso l’impiego di metodi statistici – questi usati, in maniera
sinergica, con approcci combinatoriali sono la base del catalyst design in silico
Chimica Metallorganica e Catalisi
Dipartimento di Fisica e Chimica dell’Università di Palermo
Chimica Computazionale e Catalisi
Metodi Modellistici
Indice
Chimica Computazionale e Catalisi
Modellistica Chimica in Catalisi
Metodi Modellistici
Chimica Metallorganica e Catalisi
Dipartimento di Fisica e Chimica dell’Università di Palermo
Chimica Computazionale e Catalisi
Metodi Modellistici
Panoramica sui Diversi Paradigmi di Calcolo
I i diversi metodi di calcolo (strutturale e meccanicistico) sono comunque
inquadrabili nell’ambito della meccanica classica o quantistica;
I nell’approccio classico gli atomi sono particelle materiali caratterizzate da
coordinate spaziali e velocità, governate da potenziali parametrizzati (force field
models): la dinamica molecolare (MD) per es. risolve l’evoluzione di un sistema
rispetto al tempo;
I con questi metodi (semplici e veloci) possono essere trattati sistemi molto
grandi: ad es. (fra i sistemi eterogeni) l’influenza della porosità sulla struttura dei
materiali e l’assorbimento e la reattività di molecole sugli stessi
Chimica Metallorganica e Catalisi
Dipartimento di Fisica e Chimica dell’Università di Palermo
Chimica Computazionale e Catalisi
Metodi Modellistici
Panoramica sui Diversi Paradigmi di Calcolo
Figure 6.2
I negli approcci MD i sistemi possono essere trattati a diversi gradi di
approssimazione (approximation level):
CH3
CH2
CH2
OH
I il propanolo sopra rappresentato può per esempio essere trattato come un
insieme di atomi o come una sequenza di 4 sfere (united-atom model)
Catalysis/ Rothenberg, ISBN 978-3-527-31824-7.
Chimica Metallorganica e Catalisi
www.catalysisbook.org
Dipartimento di Fisica e Chimica dell’Università di Palermo
Chimica Computazionale e Catalisi
Metodi Modellistici
Panoramica sui Diversi Paradigmi di Calcolo
I anche i metodi Monte Carlo (MC) permettono di trattare sistemi piuttosto estesi
generalmente con un piccolo dispendio di tempo di calcolo;
I questi approcci – che lavorano sfruttando la teoria della probabilità – permettono
di simulare, ottimizzandone la stabilità energetica, le più disparate proprietà
caratterizzanti un dato sistema;
I la probabilità di esistenza del sistema (in studio) quando la sua energia
potenziale è U può essere scritta come:
P(U) ∝ exp − KUT
B
I i metodi MC generalmente non permettono la trattazione dinamica delle
proprietà del sistema per il quale sono applicati;
I un’eccezione è rappresentata dai metodi time dependent (tdMC), oggi più
conosciuti come kinetic (KMC)
Chimica Metallorganica e Catalisi
Dipartimento di Fisica e Chimica dell’Università di Palermo
Chimica Computazionale e Catalisi
Metodi Modellistici
Panoramica sui Diversi Paradigmi di Calcolo
I per avere informazioni sulle proprietà elettroniche dobbiamo far riferimento alla
Figure
6.3
meccanica quantistica (QM);
I
gli approcci Hartree-Fock (HF) e post-HF come anche quelli DFT sono (oggi)
color fig
comunemente usati nello studio di sistemi catalitici;
I data l’estensione dei sistemi considerati sono sempre più usati metodi ibridi
QM/MM, QM/QM, CP-MD:
I approcci multi-scala sono interessanti per valutare, a diversi livelli di
approssimazione, proprietà che vanno dal livello atomistico a quello bulk ;
I i modelli trattati ad alto livello (generalmente gas-phase model) devono
essere ben calibrati per non portare a conclusioni erronee
Chimica Metallorganica e Catalisi
Dipartimento di Fisica e Chimica dell’Università di Palermo
Chimica Computazionale e Catalisi
Metodi Modellistici
Figure 6.4
Panoramica sui Diversi Paradigmi di Calcolo
I metodi classici (MD, MC) possono essere usati per trattare sistemi di grandi
dimensioni:
I gli effetti di bordo (sempre presenti, anche in modelli di grandi dimensioni)
possono essere minimizzati attraverso l’applicazione di “periodic boundary
conditions”
Chimica Metallorganica e Catalisi
Dipartimento di Fisica e Chimica dell’Università di Palermo
Chimica Computazionale e Catalisi
Metodi Modellistici
Panoramica sui Diversi Paradigmi di Calcolo
I analisi MC sono state usate per spiegare le proprietà di diversi sistemi catalitici;
I studi MC hanno, ad esempio, permesso di spiegare l’effetto finestra (window
effect)Figure
per il quale
6.5 nel corso di cracking catalitico su zeoliti, di diversa natura e
provenienza, si ottiene una distribuzione bidimensionale delle frazioni (di
colour fig
idrocarburi) prodotte:
I lo studio, incidentalmente, ha anche portato all’individuazione di un
meccanismo di cracking che è peculiare delle specie di maggiori
dimensioni: questo inizialmente avviene sulla “bocca” dei pori (da cui
originano i prodotti di dimensioni maggiori), per poi continuare nei canali
della zeolite (con ciò originandosi le specie di peso molecolare minore)
Chimica Metallorganica e Catalisi
Dipartimento di Fisica e Chimica dell’Università di Palermo
Chimica Computazionale e Catalisi
Metodi Modellistici
Panoramica sui Diversi Paradigmi di Calcolo
I loFigure
studio 6.6
QM può entrare nel dettaglio atomistico di un processo:
CH2=CH2
agostic
interaction
H
M
polymer
M
polymer
H
M
M
polymer
H
polymer
4-centre
transition state
reactants
+
Ln[M]
insertion TS
R
Ln[M]
Ln[M]
R
R
π -complex
activation
barrier
Ln[M]
R
insertion product
I la comprensione del meccanismo di una reazione importante come quella
di polimerizzazione è ad es. di enorme importanza;
Catalysis/ Rothenberg, ISBN 978-3-527-31824-7.
www.catalysisbook.org
I lo
studio teorico del meccanismo di Cossee e Arlman nelle reazioni di
polimerizzazione ha permesso fra l’altro d’individuare gli intermedi agostici
Chimica Metallorganica e Catalisi
Dipartimento di Fisica e Chimica dell’Università di Palermo
Chimica Computazionale e Catalisi
gure 6.7
Metodi Modellistici
Panoramica sui Diversi Paradigmi di Calcolo
I in un altro esempio – analizzato attraverso non-local DFT – il cloruro di palladio
catalizza l’ossidazione da alcol ad aldeidi o chetoni in 1,2-di-cloro-etano;
I il ciclo catalitico globale è un processo one-pot che produce l’ossidazione e la
declorinazione alifatica del di-cloro-etano:
CH2=CH2
+ base HCl
PdIICl2
OH
R
R'
O
Cl
+ base
Cl
HPdIICl
R
R' + HCl
I sono stati ipotizzati due meccanismi che implicavano:
• l’inserzione di HPd(II)Cl nel legame C – Cl e la successiva estrazione di HCl;
• l’astrazione di HCl da HPd(II)Cl seguita dall’inserzione ossidativa dello ione
Pd(II) nel legame C – Cl;
I il primo meccanismo è risultato più convincente ed è stato perciò usato
Pd(II)Cl2
nello studio del processo catalitico CH3 OH −−−−−−−→ H2 C –
–O
ClCH2 CH2 Cl
Chimica Metallorganica e Catalisi
Dipartimento di Fisica e Chimica dell’Università di Palermo
Chimica Computazionale e Catalisi
Metodi Modellistici
Panoramica sui Diversi Paradigmi di Calcolo
I metodi QM e specificatamente DFT sono oggi usati anche per lo studio di
sistemi catalitici eterogenei; fra gli altri sono stati studiati:
• il processo Haber;
• il processo Fischer-Tropsch;
• processi d’idrogenazione di idrocarburi insaturi;
• processi d’ossidazione di idrocarburi;
• processi di ossidazione di alcoli e zuccheri;
• processi di cracking e reforming;
• più in generale, l’influenza della popolazione dello spazio conformazionale di uno
o più substrati nelle trasformazioni catalitiche
Chimica Metallorganica e Catalisi
Dipartimento di Fisica e Chimica dell’Università di Palermo
Chimica Computazionale e Catalisi
Metodi Modellistici
Modellistica Predittiva e Progettazione di Catalizzatori
Figure
6.8modellistica predittiva si individuano 3 regioni, che includono “tutte le
I nella
possibili strutture catalitiche utili per un dato processo”, “tutti i possibili descrittori
utili a caratterizzare una data trasformazione” e “tutte le possibili proprietà che
possono essere studiate in relazione alla alla stessa trasformazione”
I un ruolo particolarmente importante è giocato dagli approcci QSAR e QSPR nel
porre una relazione fra gli ultimi due ambiti:
A
Catalysts
B
Descriptors
C
l’approccio è più praticabile in studi di catalisi omogenea
Chimica Metallorganica e Catalisi
Figures of merit
Dipartimento di Fisica e Chimica dell’Università di Palermo
Chimica Computazionale e Catalisi
Metodi Modellistici
Figure 6.9
Modellistica Predittiva e Progettazione di Catalizzatori
I descrittori 3D:
X
α1
β3
P
Rh
O
νCO
β1
C
X
α3
α2
β2
PR3
Rh
PR3
X
S4’ = α1+α2+α3-β1-β2-β3
Cl
CF3
70
Me
60
Me2Ph
S4’(deg.)
50
40
30
20
10
iPr
Ph2Me
EtCN
Bz o-Tol
Ph
nPr
Et
tBu
nBu
p-Tol
Cy
0
2060
2080
2100
2120
2140
2160
2180
SEP cm-1
Chimica Metallorganica e Catalisi
Dipartimento di Fisica e Chimica dell’Università di Palermo
Chimica Computazionale e Catalisi
Figure 6.10
Metodi Modellistici
Modellistica Predittiva e Progettazione di Catalizzatori
I descrittori 3D:
N
Figure 6.11
A
Cl
*
B
O
A
C
N
*
N
O
N
O
+
Cl
D
O
O
C
Cl
O
B
D
Catalyst
O
N
O
O
R R
O
O
N
N
Cu
Catalysis/ Rothenberg, ISBN 978-3-527-31824-7.
Chimica Metallorganica e Catalisi
www.catalysisbook.org
Dipartimento di Fisica e Chimica dell’Università di Palermo
Chimica Computazionale e Catalisi
gure
6.13
Metodi
Modellistici
Modellistica Predittiva e Progettazione di Catalizzatori
I descrittori 2D (e.g. adjacency, distance, detour matrices):
ΔP1-P2
DP1-P2
P
ysis/ Rothenberg, ISBN 978-3-527-31824-7.
Chimica Metallorganica e Catalisi
P
01000000000
10100000000
01010010000
00101000000
00010100011
00001010000
00100101000
00000010100
00000001000
00001000000
00001000000
www.catalysisbook.org
Dipartimento di Fisica e Chimica dell’Università di Palermo
Chimica Computazionale e Catalisi
Metodi Modellistici
Modellistica Predittiva e Progettazione di Catalizzatori
Figure 6.14
I la precisione e l’accuratezza sui descrittori è sempre correlata alla difficoltà nel
loro ottenimento:
100,000
2D
topological
descriptors
Ligands analysed /h
10,000
1,000
100
10
3D
molecular
mechanics
3D
PM3 semiempirical
3D
ab initio
method
i calcoli sono fatti su un desktopComputational
computer con
un processore a 2.5 GHz
Chimica Metallorganica e Catalisi
Dipartimento di Fisica e Chimica dell’Università di Palermo
Chimica Computazionale e Catalisi
Metodi Modellistici
Modellistica Predittiva e Progettazione di Catalizzatori
Figure
6.20 riassume l’approccio modellistico-predittivo:
I la flow-chart
seguente
START
A virtual library
containing 107
ligand-metal
complexes
create
catalyst library
select subset
for 2D models
analyse and
choose new set
Feed back
figures of
merit
and update
models
analyse using
3D models
make and test
new generation
No
Refine using
GAs and
metamodelling
The 2D models select
subsets of 10,000
catalysts
The best 500 catalysts from the 2D
models are chosen for the next step
The best 20 catalysts from
the 3D models are then
synthesised and tested
optimal
performance?
Yes
END
Chimica Metallorganica e Catalisi
Dipartimento di Fisica e Chimica dell’Università di Palermo
Appendix
Bibliografia di Base
Libri di Base Suggeriti per il Corso
Gary L. Miessler, Donald A. Tarr;
Chimica Inorganica, IV edizione;
Piccin Nuova Libraria, 2011
Gadi Rothemberg;
Catalysis: Concepts and Green Applications;
Wiley-VCH, 2008
Chimica Metallorganica e Catalisi
Dipartimento di Fisica e Chimica dell’Università di Palermo