Elettronica T - Lanzoni
Sommatore
IR4
v2
v3
v1 v2 v3
v
+
+
= − O = iR 4
R1 R2 R3
R4
R4
I1
R1
I2
R2
I3
R3
ΣIi
v
v
v
⇒ vO = − R4 1 + 2 + 3
R1 R2 R3
VO
+
_
v1
Σii =
se R1 = R 2 = R 3 = R4 :
vO = −(v1 + v2 + v3 ) = −∑ v i
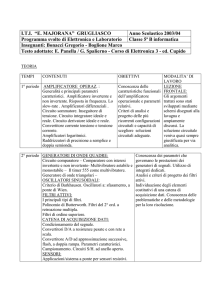
Una estensione del circuito amplificatore invertente ad operazionali è il circuito
sommatore.
Il funzionamento di questo circuito risulta intuitivo se si considerano le correnti che
fluiscono sui rami dei vari ingressi e sul ramo di retroazione.
La funzione di somma è realizzata nel nodo di massa virtuale.
In questo nodo vale infatti (per KCL):
∑i = 0
∑i
⇒
i
= iR 4
Se esprimiamo tutte le correnti in funzione della caduta sulle resistenze risulta:
vi
∑R
i
=−
vOUT
R4
da cui, se tutte le resistenze sono uguali, risulta immediatamente che :
vOUT = −∑ v i
1
Elettronica T - Lanzoni
Sommatore con guadagno
R3
v2
R1
R2
+
_
v1
VO
Es.
R1=1K Ω
R2=100K Ω
R3=10KΩ
Per v2=0 vOUT /v1 = -R3/R1 = -10
Per v1=0 vOUT /v2 = -R3/R2 = -0.1
E quindi per sovrapposizione degli effetti:
vOUT = -10v1 -v2/10
Naturalmente se le resistenze non sono tutte identiche, è possibile amplificare (o
attenuare) i segnali ai vari ingressi, scegliendo opportuni rapporti fra la resistenza di
retroazione e quelle di ingresso.
Il circuito sarà quindi caratterizzato da diversi guadagni, a seconda dell’ ingresso
considerato.
2
Elettronica T - Lanzoni
Amplificatore differenziale ad OPAMP
In molti campi è necessario ricorrere ad amplificatori differenziali ove:
vOUT = A(v2 − v1 )
Un amplificatore differenziale risulta utile per esempio nel caso di una linea rumorosa
per eliminare i disturbi di modo comune.
Per ottenere una relazione ingesso-uscita come quella voluta si può usare uno
schema come quello di figura.
In particolare, il circuito illustrato può essere pensato come la combinazione di un
amplificatore invertente (ingresso v1) ed uno non invertente (ingresso v2).
La tensione in uscita può quindi essere facilmente espressa in funzione delle tensioni
v1 e v2 applicando il principio di sovrapposizione degli effetti.
3
Elettronica T - Lanzoni
Amplificatore differenziale ad OPAMP
vO1 = −
R2
v1
R1
R4 R1 + R2
1 + R2 R1
= v2
vO 2 = v2
1 + R3 R4
R3 + R4 R1
Analizziamo quindi i due segnali separatamente.
1) Annulliamo v2 per trovare la relazione vOUT - v1 .
In questo caso, essendo nulla la corrente in ingresso al morsetto non invertente dell’
operazionale ideale, il suo potenziale è nullo. Il circuito è quindi un amplificatore
invertente con guadagno AV1= -R2/R1.
2) Annulliamo ora v1 e calcoliamo la relazione vOUT - v2.
Consideriamo la tensione v+ del morsetto non invertente. La relazione vOUT-v+ è quella
dell’ amplificatore non invertente con ingresso v+ :
vO 2 = v+
Ma
v+ = v2
e quindi
vO 2
R1 + R2
R1
R4
R3 + R4
R4 R1 + R2
1 + R2 R1
= v2
= v2
1 + R3 R4
R3 + R4 R1
4
Elettronica T - Lanzoni
Amplificatore Differenziale ad OPAMP
Sommando i contributi si ottiene:
vOUT = vO1 + vO 2 = −
R2
1 + R2 R1
v1 +
v2
R1
1 + R3 R4
Si vuole che la componente di modo comune non venga
amplificata. Perciò:
v1 = v2 ⇒ vOUT = 0
Ciò si verifica se : R2/R1 = R4/R3
A questo punto per ottenere la relazione complessiva ingressi-uscita, sommiamo i due
contributi.
Si nota che, se non si fa nessuna ipotesi sulle resistenze, risulta:
vOUT = vO1 + vO 2 = −
1 + R2 R1 R2
R2
− v2
(v1 − v2 ) +
R1
1 + R3 R4 R1
L’ uscita risulta quindi affetta da una componente non differenziale.
Per annullare questa componente si annulla il termine che moltiplica v2.
1 + R2 R1 R2
− = 0 ⇔
1
+
R
R
R1
3
4
R2 R4
=
R1 R3
Se questa condizione è soddisfatta, l’ amplificatore è puramente differenziale con
guadagno -R2/R1.
5
Elettronica T - Lanzoni
Circuito equivalente della linea disturbata
Una linea disturbata da una componente di modo
comune può essere schematizzato come segue:
L’ amplificatore differenziale permette di ottenere un segnale single ended non affetto
da eventuali componenti di modo comune che possono derivare da un disturbo
iniettato su una linea di trasmissione.
6
Elettronica T - Lanzoni
Amplificatore differenziale: Rin
Per valutare Rin scriviamo l’ equazione della maglia di
ingresso:
v2 − v1 = R1i + 0 + R1i ⇒ Rin = 2 R1
Per calcolare la resistenza di ingresso del circuito, ricorriamo al concetto di
cortocircuito virtuale degli ingressi dell’ operazionale.
In questa condizione, la resistenza di ingresso risulta semplicemente:
Ri = 2R1
Una importante considerazione è che Rin può essere in generale bassa. Questo può
essere un grosso limite specialmente in applicazioni, come la strumentazione, nelle
quali si richiede che l’ impedenza di ingresso sia elevatissima, per non perturbare il
funzionamento del circuito cui l’ amplificatore è collegato.
E’ necessario in questi casi ricorrere ad un circuito in cui i segnali siano applicati
direttamente a morsetti di ingresso di un operazionale e che allo stesso morsetto non
giungano altri rami del circuito.
Un altro punto debole di questo circuito è che volendone variare il guadagno si deve
modificare il valore di due resistenze e fare in modo che dopo la variazione sia
verificata la condizione di uguaglianza fra rapporti di resistenze.
7
Elettronica T - Lanzoni
Amp. Differenziale per Strumentazione
Un circuito che elimina i problemi visti in precedenza è quello in figura.
In esso gli ingressi sono collegati ai morsetti non invertenti di due operazionali, e
quindi viene soddisfatta la condizione di altissima impedenza di ingresso.
Inoltre, come vedremo, il guadagno può essere variato agendo sul valore di R1,
lasciando invariate le altre resistenze.
Anche in questo caso il funzionamento del circuito può essere descritto sommando i
contributi dei due segnali quando uno è stato annullato.
Partiamo per esempio da v1 annullando v2 (v2=0V).
Il morsetto invertente di A2 si trova al potenziale di massa (massa virtuale). All’ uscita
di A1 avremo quindi v1 amplificato dall’ amplificatore non invertente costituito da A1
retroazionato da R2 ed R1. Risulta quindi:
R1 + R2
vo1 = v1
R1
8
Elettronica T - Lanzoni
Amp. Differenziale per strumentazione
In uscita ad A2 avremo invece
vo 2 = −v1
R2
R1
A2 nei confronti di v1 si comporta infatti come un amplificatore invertente con guadagno
pari a -R2/R1 .
vo1 e vo2 sono portati in ingresso ad un amplificatore differenziale a guadagno pari
A -R4/R3 (vedi circuito precedente).
La componente in uscita all’ intero circuito dovuta a v1 è quindi:
vo = −
R4
(vo1 − vo 2 ) = −v1 R4 1 + 2 R2
R3
R3
R1
Una analisi perfettamente simmetrica, a meno del segno, può essere fatta per v2 una
volta annullato v1. Il suo contributo al segnale in uscita risulta:
vo = v2
R4 2 R2
1 +
R3
R1
Sommando i contributi si ottiene infine:
vo = −(v1 − v2 )
R4 2 R2
1 +
R3
R1
9
Elettronica T - Lanzoni
Configurazioni con impedenze
Z2(s)
Z1(s)
+
_
Vin(s)
Vout ( s ) = −
Vout(s)
Z 2 (s)
Vin ( s )
Z1 ( s )
Una immediata e notevole estensione dell’ amplificatore invertente è il caso in cui al
posto di due resistenze ci siano due impedenze.
In questo caso la funzione di trasferimento risulta:
H (s) = −
Z 2 (s)
Z1 ( s )
Risulta quindi abbastanza semplice costruire amplificatori con funzioni di
trasferimento anche abbastanza complesse scegliendo opportunamente le impedenze
Z1 e Z2.
10
Elettronica T - Lanzoni
Configurazioni con impedenze
1/sC
R
1/sC
R
+
_
+
_
-20 dB/dec
o
-6 db/ottava
Integratore invertente (*)
+20 dB/dec
o
+6 db/ottava
Derivatore invertente
Casi notevoli sono quelli riportati in figura.
Integratore invertente
In questo caso è
Z 2 (s) =
1
sC
e
Z1 ( s ) = R
La funzione di trasferimento risulta quindi quella di un integratore invertente:
vOUT ( s )
1
=−
vIN ( s )
sCR
Derivatore invertente
In questo caso è
Z 2 (s) = R
e
Z1 ( s ) =
1
sC
La funzione di trasferimento risulta quindi quella di un derivatore invertente:
vOUT ( s )
= − sRC
v IN ( s )
11
Elettronica T - Lanzoni
Integratore di Miller
Rf
Rf
Vout ( s)
1
=−
Vin ( s)
R 1 + sR f C
1/sC
R
ADC = -Rf/R
ω-3dB = 1/RfC
+
_
Stadio passa basso
L’ integratore presentato in precedenza, pur essendo concettualmente molto semplice,
ha due gravi difetti:
1) in DC il condensatore è un aperto e quindi l’ operazionale non risulta più
retroazionato.
2) in condizione di riposo (vIN=0) , la corrente di polarizzazione dell’ ingresso risulta in
una deriva della tensione in uscita (si integra una costante) che finisce per saturare.
Per queste ragioni, si pone in parallelo al condensatore un resistore (di valore elevato)
che permette di superare questi problemi.
La funzione di trasferimento del circuito è quindi sempre a singolo polo, ma non più
nell’ origine ma a pulsazione
ω = 1R C
f
che, se Rf è di valore sufficientemente elevato, risulta bassissima.
D’altra parte, in condizioni di riposo la tensione di uscita risulta pari a RfI-. Questo
valore di offset dovuto alla I- può non essere trascurabile se Rf è troppo elevato.
N.B. un circuito di questo tipo può essere anche interpretato come un filtro passabasso con modulo della FDT a centro banda non unitario ma pari a Rf/R.
12
Elettronica T - Lanzoni
Filtraggio di un segnale
Digitale
S/H
ADC
MEM
DSP
DAC
Sout
Sin
H(jω)
Analogico
In numerose occasioni può essere necessario filtrare un segnale, ovvero farlo passare
attraverso un circuito con una funzione di trasferimento (distorcente) che ne elimini
delle componenti spettrali e/o ne isoli altre.
Un caso tipico è l’ eliminazione della componente a 50 Hz dovuta alla rete, oppure l’
eliminazione delle componenti al di fuori di un banda di interesse ecc.
A questo problema esistono due soluzioni:
1) soluzione basata su una elaborazione digitale di un insieme di campioni
2) soluzione basata sul progetto di un circuito che abbia la FDT voluta.
Il primo approccio, sebbene più complesso e costoso, ha l’ indubbio vantaggio di una
estrema flessibilità che permette di adattare (anche dinamicamente) lo stesso circuito
a diverse esigenze semplicemente agendo sul software del DSP.
Il secondo approccio è viceversa più rigido, ma può essere più economico e
permettere di elaborare segnali con bande passanti molto estese.
13
Elettronica T - Lanzoni
Filtri passivi
I filtri passivi hanno guadagno di centro banda unitario
ES.Filtro passa basso passivo
|H(jω)|, dB
0dB
H ( jω ) =
1
1 + jωCR
Si può trarre spunto dalla considerazione appena fatta per introdurre una importante
categoria di circuiti basati su operazionali : i filtri attivi
Questi circuiti sono caratterizzati da una funzione di trasferimento con un polo o uno
zero (filtri del primo ordine) o da più poli e zeri (filtri di ordine superiore) e da un
guadagno in centrobanda maggiore di uno.
I vantaggi di un approccio ad operazionali nel progetto di un filtro sono notevoli ed in
particolare:
• Facile combinazione di più stadi per ottenere FDT complesse
•Guadagno a centro banda > 0dB
Facciamo un esempio: il filtro passa basso.
Un circuito di questo tipo, realizzato con componenti passivi, realizza una funzione di
trasferimento che ha guadagno unitario (0dB) a bassa frequenza e pendenza di 20dB/dec al di sopra della pulsazione di taglio ω0.
14
Elettronica T - Lanzoni
Filtri passivi
Combinando più filtri si ottiene una FDT diversa dal
prodotto delle FDT dei singoli stadi filtro
Supponiamo ora di voler combinare più filtri collegandoli in cascata. In questo caso, la
funzione di trasferimento dei singoli blocchi è influenzata dal rapporto impedenza di
uscita- impedenza di ingresso, esattamente come abbiamo già commentato nel caso
degli amplificatori in cascata. In questo caso però, trattandosi in generale di
impedenze complesse, la funzione di trasferimento sarà caratterizzata da frequenze
dei poli e degli zeri in generale diverse da quelle della FDT degli stadi separatamente
analizzati ed inoltre l’ attenuazione a centro banda non sarà in generale 0dB, ma,
come nell’ esempio di figura, minore.
L’ esempio riportato in figura mostra le FDT di:
• un filtro RC passa basso con R=10KΩ, C=1nF che, non caricato, ha un polo a circa
16 KHz, (curva blu),
•un filtro RC passa alto con R=10KΩ, C=1µF caratterizzato da un polo a circa 16 Hz,
(curva rossa)
•il filtro ottenuto dalla cascata dei due ha attenuazione a centro banda pari a 6dB e poli
a circa 7.9 Hz e 31.4 KHz (curva verde)
15
Elettronica T - Lanzoni
Filtri attivi: caratteristiche
+
+
+
+
Guadagno di centrobanda > 1
Bassa impedenza di uscita (componibilità)
Compattezza
Particolarmente utili a bassa frequenza
- Single ended
VI
PF
VO
VI
AF
VO
In generale, scegliendo opportunamente le reti di retroazione e componendo diversi
stadi in cascata è possibile realizzare funzioni di trasferimento di filtro complesse, in
modo relativamente semplice.
In particolare è possibile realizzare funzioni di trasferimento simili a quelle proprie di
circuiti con induttori, facendo uso di sole resistenze e capacità, o, addirittura di sole
capacità. Questo risulta di fondamentale importanza in quanto permette di realizzare
filtri di dimensioni estremamente compatte, in tecnologia film spesso o, nel caso di filtri
a capacità commutate in tecnologia del silicio monocristallino.
16
Elettronica T - Lanzoni
Filtri attivi del primo ordine
Filtro passa basso attivo
I1
I2
vi/R1 = -vO/(R2//C)
I1
I2
vi
R + 1 / jωC
1 + jωR2C
= −vO 2
= −vO
R1
R2 / jωC
R2
⇒
vO ( jω )
R
1
= H ( jω ) = − 2
vi ( jω )
R1 1 + jωCR2
La stessa FDT del filtro passa-basso, ma con guadagno a bassa frequenza maggiore
di uno, può essere realizzata con uno schema identico a quello già presentato come
integratore di Miller.
Notiamo che la FDT è a singolo polo, ma il modulo del guadagno è pari a R2/R1.
Inoltre, grazie alla bassa impedenza di uscita dell’ operazionale, il blocco manterrà
invariata la sua FDT anche se in cascata verrà posto uno o più successivi blocchi di
filtri attivi.
17
Elettronica T - Lanzoni
Filtri attivi del primo ordine
Filtro passa alto attivo
vI
1/sC
vx
vO
+
_
vX
sCR3
=
vI 1 + sCR3
R3
R1
vO R1 + R2
=
vX
R1
R2
⇒
vO ( jω )
R + R1 jωCR3
= H ( jω ) = 2
v I ( jω )
R1 1 + jωCR3
Il filtro passa alto si può ottenere combinando un passa alto passivo ad uno stadio di
guadagno (amplificatore non invertente).
18
Elettronica T - Lanzoni
Filtri attivi del secondo ordine
Un interessante filtro del secondo ordine è quello riportato in figura.
Questo circuito è anche noto come filtro universale. Esso infatti può essere utilizzato
sia come filtro passa basso o passa alto del secondo ordine sia come passa banda o
elimina banda. Di questo filtro esistono forme integrate a basso costo.
In breve il suo funzionamento può essere descritto come segue.
Si parte dall’ espressione di un filtro passa alto del secondo ordine:
Ks 2
= 2
2
Vi
s + s(ω 0 Q ) + ω 0
Vhp
Osserviamo che questa espressione puo’ essere anche scritta come:
2
1 ω0
ω 0
Vhp = KVi − Vhp − 2 Vhp
Q s
s
ovvero Vhp può essere espressa come la somma del segnale in ingresso e dei suoi
integrali, singolo e doppio.
19
Elettronica T - Lanzoni
Filtri attivi del secondo ordine
vy
ω0 =
1
CR
Rf
R1
R R f R1
Q = 1 + 3 ⋅
R2 R f + R1
E’ possibile costruire un circuito a operazionali che realizzi questa funzione
impiegando due integratori ed un sommatore (KHN biquad).
Questa cella del secondo ordine è dovuta a Kerwn Huelsman e Newcomb.
Osserviamo che fra i vari nodi del circuito e l’ ingresso corrisponde una diversa
funzione di trasferimento (LP, HP, BP) che possono essere eventualmente combinate
mediante un sommatore con guadagno.
Il funzionamento del circuito si ottiene combinando le seguenti equazioni:
Vi − V y Vy − Vbp
=
R
R3
2
Vlp − V y V y − Vhp
=
R1
Rf
Vhp
Vbp = −
sRC
Vbp
Vlp = − sRC
R3 R f
1 +
⇒ Vhp =
R2 + R3
R1
R
R2 R f ω 0
Vi +
1 +
− Vhp − f
R2 + R3
R1 s
R1
ω02
2 Vhp
s
20
Eliminando Vy si ottengono le FDT fra Vi ed i nodi Vlp, Vhp e Vbp:
H lp =
R3 (R f + R1 )
D
, H bp =
CRR3 (R f + R1 )⋅ s
D
, H hp =
C 2 R 2 R3 (R f + R1 )⋅ s 2
D
con D = C 2 R 2 R1 (R2 + R3 ) ⋅ s 2 + CRR2 (R f + R1 )⋅ s + R f (R2 + R3 )
Esprimiamo ora il fattore di qualità Q, il guadagno K e la pulsazione ω0 in funzione dei
valori degli elementi passivi.
Partiamo dal denominatore:
C 2 R 2 R1 (R2 + R3 ) ⋅ s 2 + CRR2 (R f + R1 )⋅ s + R f (R2 + R3 )
2 2
dividiamo per C R R1 (R2 + R3 ):
s2 +
R2 (R f + R1 )
CRR1 (R2 + R3 )
⋅s+
Rf
2
C R 2 R1
sostituiamo CR=1/ω0 :
s2 +
R2 (R f + R1 )
R1 (R2 + R3 )
⋅ω0 s +
Rf
R1
ω02
infine uguagliamo le due forme:
s2 +
R2 (R f + R1 )
R1 (R2 + R3 )
⋅ω 0 s +
Rf
R1
ω02 = s2 + s
ω0
Q
+ ω0
2
otteniamo :
Rf
R1
=1 ⇒
R3
1
= 2Q − 1 ⇒ K = 2 −
R2
Q
Infine la somma pesata delle tre uscite della cella biquad permette di ottenere una
funzione molto flessibile che po’ ridursi ad un qualsiasi filtro del secondo ordine
scegliendo opportunamente le resistenze:
(
Vo
RF RH )s 2 − s(RF RB )ω 0 + (RF RL )ω 0
= −K
ω
2
Vi
s 2 + s 0 + ω0
Q
2
21
Elettronica T - Lanzoni
Sintesi di impedenze: induttore simulato
La realizzazione di induttori è essenziale per la
costruzione di filtri
Gli induttori passivi per impiego a bassa frequenza
sono ingombranti
Si cerca di simulare il comportamento di un induttore
con un circuito a OPAMP, R e C
L’ ultimo elemento che rimane da sintetizzare è l’ induttore. Questo componente è
indispensabile per la costruzione dei filtri, ma al tempo stesso è ingombrante, se
realizzato come discreto, e non integrabile (almeno per valori relativamente alti).
Si cerca quindi di sostituirlo con un equivalente elettronico.
22
Elettronica T - Lanzoni
Il circuito di Antoniu
2
1
3
4
5
Il circuito di figura presenta ai morsetti di ingresso una impedenza ZIN equivalente ad un
induttore.
Per dimostrarlo, teniamo presente che gli operazionali lavorano nella zona ad alto
guadagno e quindi si ha cortocircuito virtuale fra i nodi 1 e 3 e fra i nodi 3 e 5.
La tensione ai capi di R5 è quindi V1 .
Seguendo la numerazione è possibile risalire alla corrente di ingresso.
L’ impedenza di ingresso risulta:
Z IN = sC4 R1 R3 R5 / R2
è quindi equivalente ad un induttore.
23
Elettronica T - Lanzoni
Cella del 2’ ordine con induttore simulato
H (s ) =
s / CR
s + s(1 CR ) + (1 LC )
2
Un esempio di applicazione del circuito di Antoniu è quello riportato in figura.
Un filtro passa banda è stato realizzato con un circuito RLC in cui l’ induttanza è stata
sostituita dal circuito di Antoniu. Inoltre un amplificatore (K) disaccoppia il nodo di uscita
dagli stadi a valle e fissa il guadagno della cella.
24
Elettronica T - Lanzoni
Circuiti a capacità commutate
(switching capacitors)
Φ1
V1
T
Φ2
M1
V2
M2
Φ1
Φ2
C
V1
In un periodo: ∆Q=C∆V
In un secondo:
Φ1
∆Q=C(V1-V2)
C V =V
C0
2
∆Q /T=fC∆V=I
=
V1
R=1/Cf
V2
V2
Φ2
VC0=V1
C
∆Q=C(V1-V2)
Uno dei passi fondamentali nella sintesi di filtri integrati è la sostituzione di componenti
passivi ingombranti (capacità e resistori di elevato valore, induttanze) con equivalenti
“elettronici”.
I moderni circuiti che sintetizzano i filtri attivi, sono costruiti in forma monolitica
sfruttando la tecnica delle capacità commutate.
Un circuito a capacità commutate è costruito in tecnologia CMOS sfruttando tre soli
elementi:
• Capacità MOS
• Amplificatori operazionali CMOS
• Interruttori CMOS (pass transistor)
Con questi elementi è possibile sintetizzare resistori ed induttori.
Resistori a capacità commutate
Un resistore può essere simulato mediante una capacità e due interruttori, che
supporremo ideali.
Il principio di funzionamento è quello della pompa di carica, ossia un dispositivo che
travasa una certa quantità di carica da un nodo ad un altro del circuito.
25
Elettronica T - Lanzoni
Filtri attivi a capacità commutate
H ( jω ) = −
R2
1
R1 1 + jωCR2
H ( jω ) = −
C1
C2
1
1 + jω
C
fC2
Una volta in grado di simulare il funzionamento di un resistore, è possibile integrare un
filtro sostituendo alle resistenze, l’ equivalente a capacità commutate.
26