Classe III A Inf : Recupero primo quadrimestre MATEMATICA
TRIGONOMETRIA
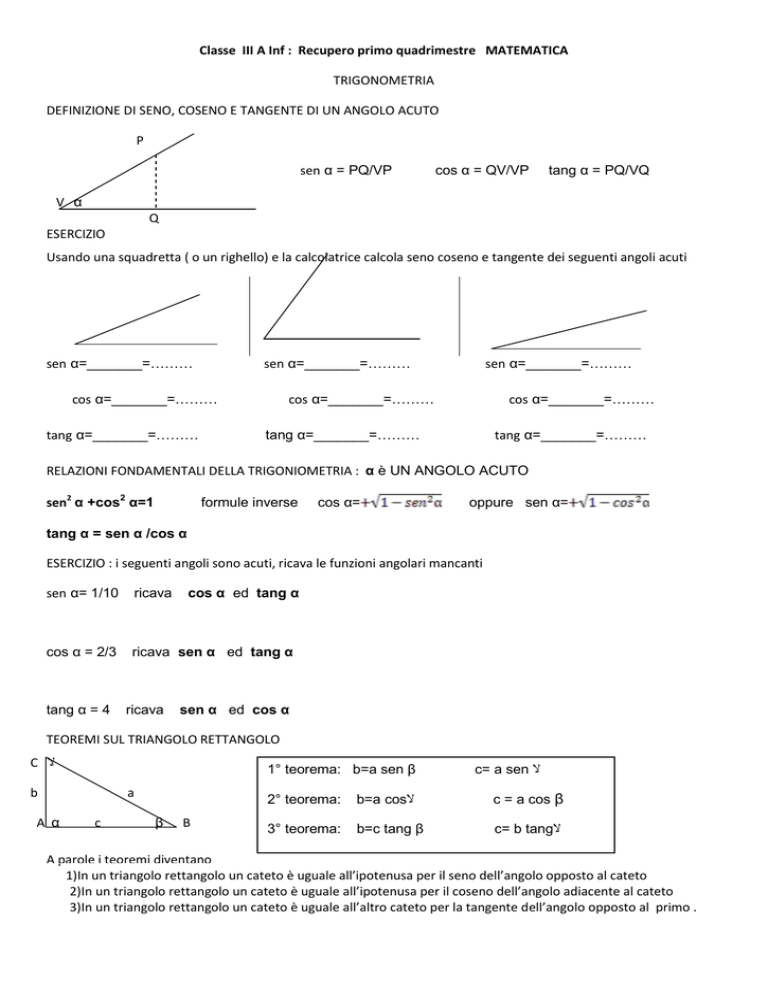
DEFINIZIONE DI SENO, COSENO E TANGENTE DI UN ANGOLO ACUTO
P
sen α = PQ/VP
cos α = QV/VP
tang α = PQ/VQ
V α
Q
ESERCIZIO
Usando una squadretta ( o un righello) e la calcolatrice calcola seno coseno e tangente dei seguenti angoli acuti
sen α=_______=………
sen α=_______=………
cos α=_______=………
tang α=_______=………
sen α=_______=………
cos α=_______=………
cos α=_______=………
tang α=_______=………
tang α=_______=………
RELAZIONI FONDAMENTALI DELLA TRIGONIOMETRIA : α è UN ANGOLO ACUTO
sen2 α +cos2 α=1
formule inverse
cos α=
oppure sen α=
tang α = sen α /cos α
ESERCIZIO : i seguenti angoli sono acuti, ricava le funzioni angolari mancanti
sen α= 1/10
ricava
cos α = 2/3
ricava sen α ed tang α
tang α = 4
ricava
cos α ed tang α
sen α ed cos α
TEOREMI SUL TRIANGOLO RETTANGOLO
C ﻻ
1° teorema: b=a sen β
b
a
A α
c
β
B
c= a sen ﻻ
2° teorema:
b=a cosﻻ
c = a cos β
3° teorema:
b=c tang β
c= b tangﻻ
A parole i teoremi diventano
1)In un triangolo rettangolo un cateto è uguale all’ipotenusa per il seno dell’angolo opposto al cateto
2)In un triangolo rettangolo un cateto è uguale all’ipotenusa per il coseno dell’angolo adiacente al cateto
3)In un triangolo rettangolo un cateto è uguale all’altro cateto per la tangente dell’angolo opposto al primo .
ESERCIZIO
Ricava le formule inverse dei tre teoremi
b= a sen β
a=________
sen β=__________
b= a cosﻻ
a=_________
cos ___________= ﻻ
b= c tang β
c=__________
tang β=____________
ESERCIZI : RISOLVI I SEGUENTI TRIANGOLI RETTANGOLI CON α=90°
DATI
Incognite
DATI
Incogn.
DATI
Incogn.
DATI
α=90°
α=90°
α=90°
α=90°
a=20 cm
c=4cm
a=26 cm
c=30cm
β= 30°
β= 60°
b= 13 cm
b=30cm
Incogn.
Risolvi le seguenti equazioni in [0;2π]:
4sen2x=1
2senx+1=0
4cos2x-1=0
3tg2x-1=0
3 - 2cosx=0
Rappresenta graficamente la
cosinusoide y=cosx e descrivi le sue
caratteristiche
3 tgx=-1
2sen2x +senx=0
3- 3 tangx=0
2sen2x-1=0
tg2x-tgx=0
2senx+ 2 =0
tgx= - 3
Rappresenta graficamente la sinusoide Rappresenta graficamente la
y=senx e descrivi le sue caratteristiche tangentoide y=tangx e descrivi le sue
caratteristiche
Esercizi di geometria analitica ( VEDERE LIBRO DI TESTO “ La geometria analitica” ALLA PAG 232 punti 2-3
Problema 1 : Dati i punti A(-3;0) B(-1;4) C(1;-1) D(-1;-5), verificare che ABCD è un parallelogramma e calcolarne il
perimetro. Determinare le coordinate dei punti medi dei quattro lati e riportarli sul grafico. Calcolare la lunghezza
del segmento BD.
Problema 2
Dato il triangolo ABC con A(-3;5) B(7;5) C(2;8) rappresentarlo graficamente. Determinare i punti A’,B’, C’
simmetrici di A,B,C rispetto al centro della simmetria M(2;6).
Rappresentare graficamente il triangolo A’B’C’. Determinare la lunghezza del segmento CC’.












