Definizione di angolo orientato:

Definizione di angolo orientato:
Un angolo si dice orientato quando è generato da una rotazione del lato
‘origine’ attorno al vertice fino ad arrivare al lato termine; cioè quando è
fissato quale dei due lati è il 1° e quale il 2°.
Si dice positivo se la rotazione è in verso antiorario, negativo se in verso
orario.
Il grado (°) è l’unità di misura dell’angolo: 1° corrisponde a 1/360° dell’angolo
giro, mentre 1° = 60’( gradi sessagesimali) e 1’= 60’’( gradi centesimali)
Es. 30°20’54’’ + 2°45’24’’ = 33°6’18’’ 
…per esprimerlo in forma decimale bisogna ricordarsi che:
1’= 1/60’’ ; 1’’= (1/60)’= (1/60+1/60)° = (1/3600)°
QUINDI…. 33°( 6/60)°(18/3600)° = 33° (1/10)° (1/200)° 
33°+0,1°+0,005°= 33,105°
…per passare da decimale a grado: 12,43°=12°+0,43x60’
= 12°+25,8’
= 12°+25’+0,8x60’’
= 12°25’48’’
IL RADIANTE:
Il radiante è la misura dell’angolo al centro
che sottende un arco lungo come il raggio.
AP(arco)/r= 1 radiante
2πr/r= 2πrad
ρ simbolo dell’ angolo espresso in radianti
ρ : 2π = α° : 360°  ρ = α°x2 π
 α°= ρ x 360°/2 π
Es.
360°= 2π
180°= π
90 °= π / 2
60° = π / 3
45° = π / 4
30° = π / 6
x:30°= 2 π : 360°
x = 30°· 2 π / 360° = π / 6
LE FUNZIONI GONIOMETRICHE
La funzione goniometrica può essere definita come rapporti fra i lati di un
triangolo rettangolo
Le funzioni goniometriche:
- seno e coseno
- tangente e cotangente
- circonferenza goniometrica
- secante e cosecante
SENO&COSENO:
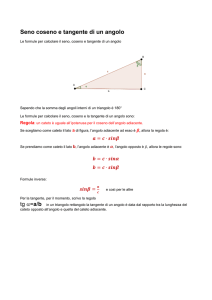
Dato il triangolo rettangolo ORP in figura, si dice seno dell'angolo α il
rapporto tra il cateto opposto all'angolo e l'ipotenusa del triangolo
senα = RP/ OP 
senα = cateto opposto/ ipotenusa
dato che la circonferenza ha raggio 1  il seno
sarà uguale a RP.
Dato sempre il triangolo in figura si dice coseno
dell’angolo α il rapporto tra il cateto adiacente e
l’ipotenusa del triangolo.
Cosα = OR/OP 
cosα = cateto adiacente/ipotenusa
… siccome la circonferenza ha raggio 1  cosα = OR
- E’ possibile dare una rappresentazione analitica delle funzioni di seno e
coseno: le due funzioni sono periodiche, perché abbiamo visto come i loro
valori si ripetano se continuiamo a girare sulla circonferenza.
Infatti crescendo oltre 360°, il seno e il coseno si ripetono uguali, si dice
perciò che le due funzioni siano funzioni periodiche di periodo 360°(2π)
Le due funzioni hanno valori sempre compresi tra -1 e 1, cioè il codominio
delle funzioni seno e coseno è l'intervallo [-1,1] dei numeri reali.
SENO 
 COSENO
LA CIRCONFERENZA GONIOMETRICA
Come circonferenza goniometrica intendiamo la circonferenza che ha come
centro l’origine O degli assi e raggio di lunghezza 1;
1^RELAZIONE FONDAMENTALE:
considerando una circonferenza di raggio 1, e un punto B a cui corrisponda
l’angolo alfa, seno coseno e raggio formeranno un triangolo rettangolo a cui
possiamo applicare il teorema di Pitagora  sen²α + cos²α = 1
OB²= OA²+ AB² sotituiamo  1 = cos²α + sen²α
che diventasen²α + cos²α = 1
( da qui possiamo ricavare poi seno e coseno)
1) senα = ± √1-√cos²α
2) cosα = ±√1-√sen²α
Es.
Senα = 7/ 25
0 < α < π/2 (90°)  cos α ?
- inanzitutto dobbiamo individuare il quadrante che sta tra 0 e 90°, cioè il
I°, dove cos>0 e sen>0
cos α = √1- (7/25)² √1- 49/625  √625-49/625  √576/625 = 24/25
LA TANGENTE E LA COTANGENTE
- la tangente goniometrica (tg α) è una delle funzioni dell’angolo alfa; viene
definita come rapporto del segmento di tangente in A alla circonferenza,
intercettato dal prolungamento del raggi 0P con il raggio OA della
circonferenza.
- La cotangente dell'angolo alfa è la funzione che all'angolo alfa associa
l'ascissa del punto T
2^ RELAZIONE FONDAMENTALE
consideriamo la circonferenza goniometrica, e notiamo che:
- i triangoli OPH e OTA sono simili ( hanno due angoli congruenti
rispettivamente e i lati in proporzione) posso così considerare che se
OH : OA = PH : TA … sostituendo
Cosα : 1 = senα : TA
... QUINDI : TA = 1 · senα / cosα = senα / cosα
Definiamo quindi la tangente cosi : tg = senα / cosα
La seconda relazione è quindi una relazione fra il
seno e il coseno con la tangente.
GRAFICI DELLE FUNZIONI GONIOMETRICHE
1. COSENO
2. SENO
3. TANGENTE
4. COTANGENTE
5. CIRCONFERENZA GONIOMETRICA
COSENO E SENO DI ANGOLI PARTICOLARI:
α in gradi
0°
α in
radianti
0
senα
cosα
Tgα
cotgα
0
1
0
_______
30°
Π/6
½
√3/2
√3/3
√3
45°
Π/4
1/2
√2/2
1
1
60°
Π/3
√3/2
1/2
√3
√3/3
90°
Π/2
1
0
Non esiste
0
120°
2/3 Π
√3/2
-1/2
- √3
√3/3
135°
3/4 Π
- √2/ 2
- √2/2
-1
-1
150°
5/ 6 Π
- √3/2
- √3/3
- √3
180°
Π
0
-1
O
________
210°
7/6 Π
- 1/ 2
- √3/2
√3/3
√3
225°
5/4 Π
- √2/2
- √2/2
1
1
240°
4/3 Π
- √3/2
-1/2
√3
√3/3
270°
3/2 Π
0
Non esiste
0
300°
5/3 Π
- √3/2
1/2
- √3
- √3/3
315°
7/4 Π
√2/2
√2/2
-1
-1
330°
11/5 Π
- 1/2
√3/2
- √3/3
- √3
360°
2Π
0
1
0
_______
1/ 2
-1