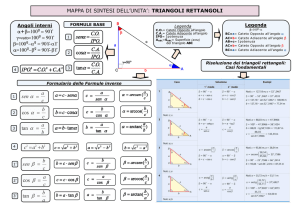
Seno coseno e tangente di un angolo
Le formule per calcolare il seno, coseno e tangente di un angolo
Sapendo che la somma degli angoli interni di un triangolo è 180°
Le formule per calcolare il seno, coseno e la tangente di un angolo sono:
Regola: un cateto è uguale all’ipotenusa per il coseno dell’angolo adiacente.
Se scegliamo come cateto il lato
a di figura, l’angolo adiacente ad esso è π·, allora la regola è:
π = π β ππππ·
Se prendiamo come cateto il lato b, l’angolo adiacente è πΆ, l’angolo opposto è π½, allora le regole sono:
π = π β ππππΆ
π = π β ππππ·
Formule inverse:
ππππ· =
π
π
e così per le altre
Per la tangente, per il momento, scrivo la regola
tg ο‘=a/b
in un triangolo rettangolo la tangente di un angolo è data dal rapporto tra la lunghezza del
cateto opposto all’angolo e quella del cateto adiacente.
