Funzione tangente e cotangente

Definizione e grafico
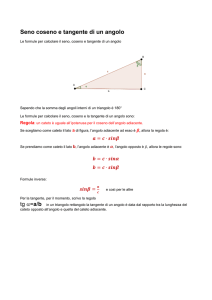
Consideriamo la nostra circonferenza
Goniometrica con il relativo angolo α:
La tangente dell’angolo α è quella
funzione che associa ad ogni angolo il
rapporto, quando esiste, tra l’ordinata
e l’ascissa di B
B
O
α
xB
yB
E
yB
tg 
xB
Anche per la tangente, così come per il seno e il
coseno, la relazione può essere estesa ad ogni
tipo di triangolo, tramite l’uso dei triangoli
simili
Poiché i triangoli OAB e OA’B’ sono
B’
α
O
B
simili, il rapporto dei lati è costante,
pertanto:
yB
AB A' B '

OA OA'
xB A
A’
La tangente di un angolo è quindi
pari al rapporto tra il cateto
opposto e quello adiacente.
Il rapporto tra ascissa ed ordinata del punto B
non esiste sempre. In particolare non è
possibile quando l’ascissa di B, ovvero il coseno
dell’angolo, è pari a zero. Ciò avviene a 90° e a
270° e si ripete ad ogni angolo giro. Possiamo
riassumere il tutto dicendo che la C.E. della
tangente è:


2
 k ; ovvero   90  k180 con k  
Riprendiamo l’uguaglianza precedente:
AB A' B'
AB y B

 OA'  1  A' B' 

 tg
OA OA'
OA xB
Quindi la tangente è, graficamente, l’ordinata del punto B’ che si ottiene intersecando il
prolungamento di OB con la perpendicolare all’asse x passante per A’.