scheda_4 - Liceo Morgagni

Scheda 4: SENO, COSENO E TANGENTE CON LA CIRCONFERENZA
GONIOMETRICA
1.
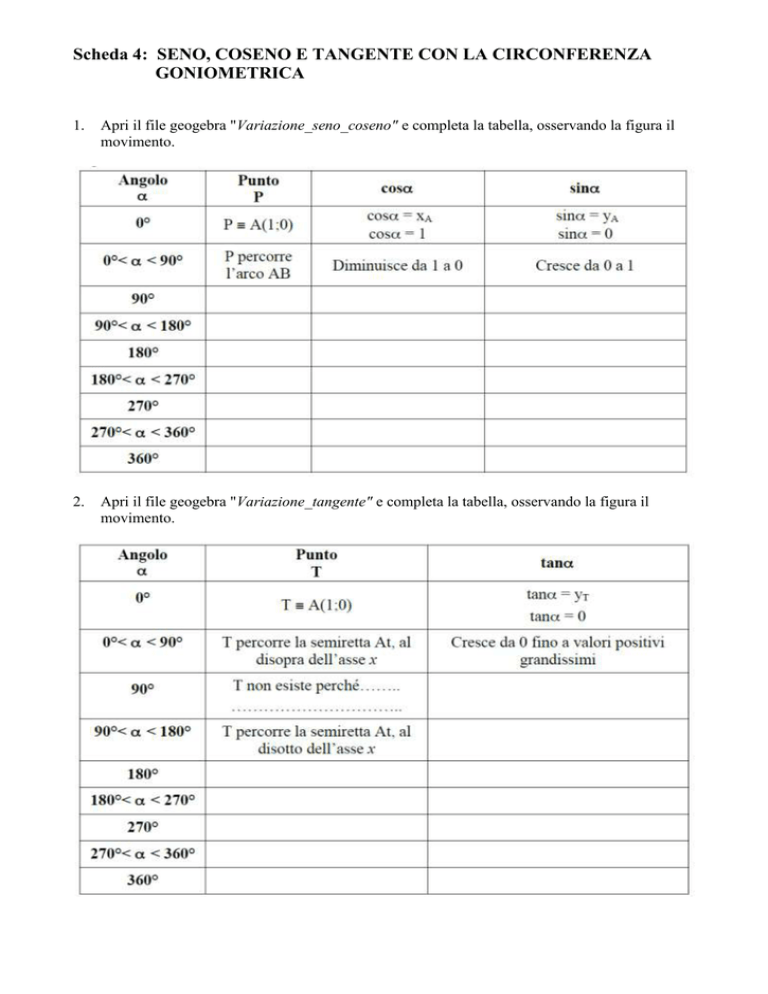
Apri il file geogebra "Variazione_seno_coseno" e completa la tabella, osservando la figura il
movimento.
2.
Apri il file geogebra "Variazione_tangente" e completa la tabella, osservando la figura il
movimento.
3.
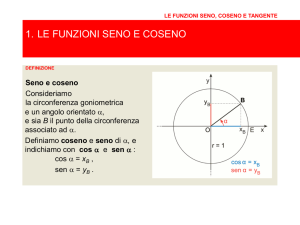
Se l'angolo α varia fra 0° e 90°, le nuove definizioni di seno, coseno e tangente ci permettono di
individuare due triangoli: OPB e OAT come mostrato in figura
Considera il triangolo OPB:
(Scrivi ciò che ti viene richiesto prima come rapporto tra segmenti
poi utilizzando le coordinate dei punti)
....... .........

 ..........
....... .........
....... .........
sen 

 ..........
....... .........
cos  
Considera il triangolo OAT:
tan  
4.
....... .........

 .........
....... .........
Completa il procedimento qui sotto per trovare una relazione che lega seno e coseno di uno
stesso angolo α.
P( xP , y P )  P(cos  , sen )
Dalla definizione di circonferenza goniometrica
il raggio OP della circonferenza misura .......
Il raggio OP risulta essere ipotenusa di un
triangolo rettangolo. Applicando il teorema di
Pitagora a tale triangolo otteniamo:
................................ = ......
In termini di seno e coseno otteniamo:
................................ = ......
5.
Completa il procedimento qui sotto per trovare una relazione che lega seno, coseno e tangente
di uno stesso angolo α.
Consideriamo la retta OP che interseca la
tangente t in T.
Possiamo ricavare la pendenza m di tale retta sia
dal triangolo OPH, sia dal triangolo OKT.
Dal primo risulta:
....... .........
m

....... .........
Dal secondo risulta:
....... .........
m

 .......
....... .........
H
K
Da cui m 
.........
 .......
.........