1 - I@PhT

Corso di Laurea in Fisica
Corso di Struttura della Materia - G. Rinaudo
Nota 3 – Transizioni termiche e statistica di Boltzmann
Transizioni
Che cosa fa sì che un elettrone si trovi in un certo livello energetico piuttosto che in un altro?
Due possibili modi di cambiare energia:
- attraverso urti: transizioni termiche
- attraverso assorbimento o emissione di radiazione elettromagnetica: transizioni radiative
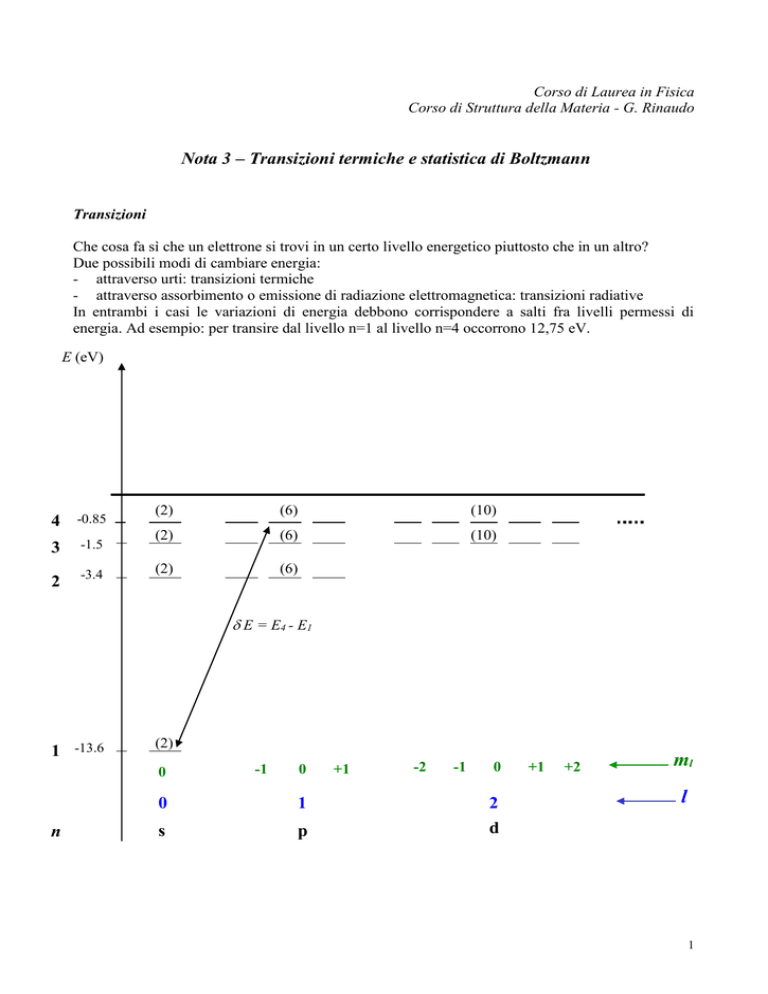
In entrambi i casi le variazioni di energia debbono corrispondere a salti fra livelli permessi di
energia. Ad esempio: per transire dal livello n=1 al livello n=4 occorrono 12,75 eV.
E (eV)
4
-0.85
3
-1.5
2
-3.4
(2)
(6)
(10)
(2)
(6)
(10)
(2)
(6)
 E = E4 - E1
1
-13.6
(2)
0
n
-1
0
+1
-2
-1
0
0
1
2
s
p
d
+1
+2
ml
l
1
Transizioni termiche
Ipotesi:
- l’atomo è immerso in un “bagno termico” a temperatura T;
- l’elettrone può scambiare energia attraverso urti con le altre particelle
(atomi, molecole, elettroni, ecc.) passando dal livello di energia Einiz al
livello Efin
Calcolo:
- utilizziamo le relazioni della meccanica statistica classica (vedremo a
posteriori che ciò è lecito per le transizioni a livello atomico o
molecolare),
- imponendo però livelli energetici quantizzati
Le basi del calcolo statistico classico rivedute in termini di stati quantizzati
Si richiede l’equilibrio statistico di N particelle su k stati possibili, raggiunto attraverso urti che
consentono lo scambio di energia. Quattro passi:
- descrizione del sistema: individuare, mediante i relativi numeri quantici, gli stati possibili
(microstati) che hanno una certa energia Ei;
- calcolare l’energia Ei dell’i-esimo stato (macrostato);
- calcolare la degenerazione gi dell’i-esimo stato;
- calcolare la probabilità di una certa partizione, cioè in quanti modi si
4
3
+3
possono disporre Ni particelle sui k stati conservando l’energia totale a
4
3
+2
disposizione (probabilità di una certa partizione di stati);
4
3
+1
- ipotesi: tutti i microstati accessibili sono egualmente probabili.
4
3
0
Esempio: microstati accessibili agli atomi di idrogeno per i primi 6 livelli
energetici (macrostati)
I microstati sono soluzioni dell’equazione di Schrodinger
 p2
L2
Ze 2 
H (r , ,  )   r 

 (r , ,  )  E (r , ,  )
 2m 2mr 2
r 

e sono descritti dalla funzione
d’onda
 (r, , )  Rn,l (r )Ylml ( , )
Parametri essenziali per la
descrizione dello stato:
numeri quantici: ni, li, mi
(ignoriamo ms che non è
essenziale ai fini del calcolo)
livello energetico: Ei
degenerazione : gi
numero di occupazione: Ni
-
E6=-0,38
6
N6
36
E5=-0,54
5
N5
25
E4=-0,85
4
N4
16
E3=-1,6
3
N3
9
E2=-3,4
2
N2
4
4
4
4
4
4
4
4
4
4
4
4
4
3
3
3
2
2
2
2
2
1
1
1
0
3
3
3
3
3
3
3
3
3
2
2
2
2
2
1
1
1
0
2
2
2
2
E1=-13,6
eV
1
i
N1
1
1
gi
n
-1
-2
-3
+2
+1
0
-1
-2
+1
0
-1
0
+2
+1
0
-1
-2
+1
0
-1
0
1
1
1
0
0
l
+1
0
-1
0
0
m
2
Statistica di Boltzmann
Il calcolo fondamentale è quello del numero di modi Wi in cui si possono disporre Ni particelle sul
livello i. Per il livello 1, in cui la degenerazione è 1, si ottiene:
W1 
N ( N  1)( N  2)( N  3)
N!

4!
N1! ( N  N1 )!
Per il secondo livello, occorre tenere conto della degenerazione g2, che è >1:
W2 
( N  N1 )!
N
g2 2
N 2!( N  N1  N 2 )!
Facendo il prodotto del numero di modi su tutti i livelli si ottiene:
N
g i
W  N!  i i
N i!
Si cerca il massimo di lnW con i vincoli sul numero totale N di particelle e l’energia totale E
(massimo vincolato):
ln W  ln N !
i Ni  N
i Ni Ei  E
i Ni ln gi  i ln Ni!
Usando il metodo dei “moltiplicatori di Lagrange”, si richiede che sia nullo ogni termine della
somma:
 d ln Wi
dN
dNi Ei 
dNi  0
 i  
dNi
dNi 
 dNi
in cui  e  sono appunto i moltiplicatori legati alla conservazione del numero totale N di particelle
e dell’energia totale E. Sviluppando i calcoli si ottiene:
i 
d ln Wi
1
 ln g i (ln N i  N i
 1)
dN i
Ni
ln g i  ln N i    Ei  0 ; ln
Ni
   E i
gi
Da cui si ottiene l’espressione generale della distribuzione di Boltzmann:
N i  Cgi e  Ei
Il parametro , che ha le dimensioni di un inverso dell’energia e descrive la condivisione
dell’energia in situazioni di equilibrio termico, viene ricondotto alla temperatura assoluta T
attraverso la costante di Boltzmann kB=8,6 10-5 eV K-1, per cui si ottiene l’espressione finale della
statistica di Boltzmann:
(1)
Ni  Cgi e Ei / k BT
La (1) mostra la caratteristica generale delle distribuzioni statistiche, valida anche per le statistiche
quantistiche: la distribuzione è il prodotto di due termini:
- il termine gi di “spazio delle fasi” o “degenerazione” del livello, che non dipende dalla
temperatura, ma solo dalle caratteristiche del macrostato di energia Ei;
3
-
il termine statistico (funzione di Boltzmann), f Btz( Ei , T )  E Ei / k BT , che dipende dall’energia
Ei, dalla temperatura T e anche dalle ipotesi fatte sul comportamento collettivo di particelle
identiche, come si vedrà trattando di statistiche quantistiche.
Esempio: distribuzione sui livelli energetici di
atomi di idrogeno a T=50000K (temperatura di
una stella?)
kBT = 8,6 10-5 eV K-1 5  104 K = 4,3 eV
i
1
2
3
4
5
6
gi
Ei
(eV)
1 -13,6
4
-3,4
9
-1,6
16 -0,85
25 -0,54
36 -0,38
fBlz(Ei,T)
(e-E/kT )
24
2,2
1,5
1,2
1,14
1,09
45
40
5  104 K
fBz
35
30
25
gl fBlz
20
24
9
13
19
28
39
gl fBz
15
10
5
0
-16
-12
-8
-4
0
E (eV)
Confronto (in scala logaritmica) fra due temperature diverse (6500 K è circa la temperatura della
superficie del Sole)
25,00
25,00
5  104 K
20,00
6,5  103 K
20,00
15,00
15,00
gl fBz
10,00
fBz
gl fBz
10,00
fBz
5,00
5,00
0,00
0,00
-14
-10
-6
E (eV)
-2
-14
-10
-6
-2
E (eV)
Un confronto simile permette, ad esempio, di determinare la temperatura alla superficie di una
stella. Supponiamo infatti che la temperatura della stella sia Tstella >> Tsole: ci aspettiamo che, in base
alla distribuzione di Boltzmann, gli stati di alta energia dell’idrogeno siano relativamente più
popolati sulla superficie della stella che sulla superficie del Sole. Se calcoliamo, ad esempio, le
popolazioni relative degli stati con n=3 e n=41 (che si può fare confrontando l’intensità relative
delle due righe spettrali dell’idrogeno nel rosso e nel verde), si ottiene, per il Sole:
N 
g
RSole   3 
 3 e( E4  E3 ) / k BTSole  2,2 , mentre per una stella, con una temperatura ad
 N 4  Sole g 4
esempio di 10000K, tale rapporto varrebbe solo 1,4: la luce del Sole è quindi più “rossa” della luce
della stella.
Una transizione radiativa dal livello 3 al livello 2 dell’idrogeno comporta l’emissione di un fotone di energia pari a
3,4-1,6=1,8 eV, che ha lunghezza d’onda   700 nm (rosso), mentre dal livello 4 al livello 2 l’energia è di 2,55 eV,
corrispondenti a 490 nm (verde).
1
4