Prodotto cartesiano - Classe delle Lauree in Scienze Biologiche

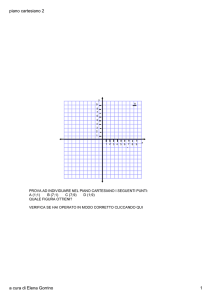
Prodotto cartesiano
Esempio 1. I gruppi sanguigni
I gruppi sanguigni AB0 si spiegano teoricamente con tre geni o allelomorfi nello stesso
locus genetico. Gli alleli si indicano con a, b, 0. Ogni gamete (uovo o spermatozoo) porta uno dei
tre alleli. Per ottenere tutte le possibilità di combinazione genetica tra gameti indichiamo con
U = {a, b, 0} = S
l’insieme degli alleli (che quindi è identico per uovo e spermatozoo) ed eseguiamo il prodotto
cartesiano
US = {<a, a>, <a, b>, <a, 0> , <b, a>, <b, b>, <b, 0>, <0, a>, <0, b>, <0, 0>}.
Rappresentazione grafica:
figura 1: prodotto cartesiano US
L’insieme US è costituito da nove coppie ordinate, poiché il numero di elementi
(cardinalità) di un prodotto cartesiano è dato dal prodotto delle cardinalità dei due insiemi dai quali
è ottenuto.
Osservazione: in questo caso particolare, per una legge genetica, l’ordine dei due alleli è irrilevante;
volendo quindi considerare l’insieme delle combinazioni effettive, diciamo G, si ha:
G = {<a, a>, <a, b>, <a, 0>, <b, b>, <b, 0>, <0, 0>}.
G è un sottinsieme di US e stabilisce una relazione tra U ed S (vedi paragrafo successivo).
Considerato che la presenza di un antigene a o b è dominante, si ottengono poi i quattro
gruppi sanguigni: A (dalle combinazioni <a, a> e <a, 0>), B (da <b, b> e <b, 0>), AB (da <a, b>)
e 0 (da <0, 0>).
Relazioni
Esempio 1: Isotopi
Sia A l’insieme degli elementi chimici secondo il numero atomico. A è un insieme finito, ma
piuttosto grande, perciò non lo elencheremo. I simboli dei suoi primi elementi sono:
H, He, Li, Be, B, C, N, O.
N, insieme dei numeri naturali, rappresenta in questo contesto l’insieme di tutti i pesi
atomici (arrotondati agli interi).
Il prodotto cartesiano AN è un insieme infinito. Dei suoi elementi, cioè delle coppie
ordinate elemento chimico - peso atomico, interessano tutti e solo quelli che esistono in natura o che
possono essere prodotti in laboratorio, vale a dire gli isotopi (stabili o instabili) di ciascun elemento
chimico.
48
Ad esempio, la coppia ordinata <He, 4> rappresenta l’isotopo dell’elio di peso 4, che nella
simbologia fisica corrente viene indicato 4He.
Le coppie ordinate di questo tipo costituiscono un sottinsieme proprio di AN, cioè una
relazione (o corrispondenza) tra A e N, che possiamo indicare con I e definire nel seguente modo:
I = {<x, n>: xA  n è il peso atomico di un isotopo di x}.
Parte di questa relazione è rappresentata in figura 2:
Figura 2: Gli isotopi stabili sono contrassegnati dai punti neri. Essi formano una relazione in AN. Gli isotopi instabili
sono contrassegnati dai punti grigi. Essi costituiscono una seconda relazione in AN. Entrambi i tipi di punti formano
una terza relazione, la relazione I illustrata sopra, unione delle prime due.
La relazione I è ovunque definita (ogni elemento chimico ha almeno un peso), ma non è
funzionale (ad esempio He ha quattro isotopi (due stabili e due instabili), quindi I non è una
funzione.
Inoltre la relazione I non è iniettiva, dato che esistono isotopi di elementi diversi che hanno
lo stesso peso atomico: ad esempio 3 è il peso di un isotopo (instabile) dell’idrogeno, ma anche di
un isotopo (stabile) dell’elio.
I non è una relazione suriettiva: infatti l’insieme N infinito, mentre l’insieme degli elementi
chimici A ha un numero finito di elementi e ciascuno di questi ha un numero finito di isotopi; perciò
ci saranno senz’altro dei numeri naturali che non compaiono come ordinata di un elemento della
relazione I; in altre parole: certi numeri naturali non sono il peso atomico di alcun isotopo
conosciuto.
La relazione opposta IopNA può essere così definita:
<n, x>Iop  esiste un isotopo di x di peso n.
Si osservi che la relazione Iop è suriettiva, poiché ogni elemento di A deve avere un peso, ma
non è iniettiva, dato che uno stesso elemento di A corrisponde in Iop ai diversi pesi dei suoi isotopi.
Esempio 2: Interazione tra neuroni (Thrall, Mortimer, Rebman e Baum, 1967, Modello CE1)
Consideriamo l’insieme
S = {a, b, c, d, e, f}
di sei neuroni (cellule nervose del cervello) indicati in ordine arbitrario. Un neurone può
trasmettere o meno un impulso ad un altro neurone. Il meccanismo di trasmissione è complesso, ma
49
sottolineiamo che l’impulso va solo in una direzione; se, ad esempio, il neurone a può mandare
impulsi al neurone b allora non può ricevere impulsi da b.
L’insieme prodotto cartesiano SS, con i suoi 36 elementi, contiene tutte le connessioni
immaginabili dei sei neuroni.
La relazione R rappresentata in figura 3 sia con grafico sagittale che cartesiano, è il risultato
delle connessioni osservate. R è un sottinsieme di SS, è costituito da dieci elementi (coppie
ordinate) e può essere così definito:
R = {<x, y>  SS: x trasmette impulsi a y} =
{<a, b>, <a, d>, <c, a>, <b, d>, <b, c>, <c, d>, <d, e>, <c, f>, <d, f>, <f, e>}.
Possiamo anche dire che
RSS e xRy  x manda impulsi a y.
Figura 3: Grafico sagittale e grafico cartesiano della relazione R
Nota: nel grafico sagittale la connessione xRy è indicata, per convenzione, con x ( y.
Osserviamo che la relazione R, in quanto relazione su S, non contiene alcun elemento della
diagonale (perché nessun neurone può trasmettere impulsi a se stesso), quindi R è antiriflessiva.
Inoltre, per la condizione posta sopra, se xRy non può essere yRx, quindi R è strettamente
antisimmetrica.
Notiamo inoltre che R non è transitiva; infatti si ha, per esempio,
aRb  bRc ma non aRc.
Dunque R non è una relazione di ordine stretto.
R non è ovunque definita, perché il neurone e non invia impulsi, e non è funzionale, visto
che, ad esempio, a è in relazione (in connessione) sia con b che con d.
R non è iniettiva: ad esempio, d riceve impulsi da più neuroni; R è suriettiva, infatti tutti gli
elementi di S elencati in verticale sono effettivamente riceventi.
La relazione Rop è così definita:
RopSS e xRy  x riceve impulsi da y.
Funzioni
Esempio 1: Sia U un insieme di persone e sia F l’insieme delle impronte digitali degli elementi
di U.
Ciascuna persona ha dieci impronte digitali e ciascuna delle impronte di F individua
univocamente la persona alla quale è stata rilevata.
50
La relazione R FU, che associa ad ogni impronta l’unica persona che può averla lasciata,
ha un notevole interesse pratico, proprio per il fatto di essere ovunque definita su F e funzionale,
cioè una funzione tra F e U.
Esempio 2: Ogni specie biologica possiede un numero di cromosomi comune a tutti gli individui
della specie (trascurando i casi patologici).
Detto S l’insieme delle specie biologiche, l’insieme delle coppie ordinate
<s, n>, dove sS e n è il numero di cromosomi di s
costituisce una relazione tra S e N (insieme dei numeri naturali)che è una funzione. Infatti tale
relazione è ovunque definita su S e funzionale.
Utilizzando la notazione insiemistica si scrive:
f:SN
s n
dove n = f (s) se e solo se n è il numero di cromosomi caratteristico della specie s.
Si osservi che tale funzione non è iniettiva, poiché specie diverse possono avere lo stesso
numero di cromosomi, e non è suriettiva, dal momento che, ovviamente, non tutti i numeri naturali
corrispondono al numero di cromosomi di qualche specie biologica.
Di conseguenza, la relazione opposta fopNS non è una funzione.
Esempio 3: (Rains, 1967)
L’autore ha osservato l’assorbimento del potassio (K) da parte del tessuto di una foglia del
mais (Zeamays) al variare del tempo t, misurato in ore (variabile indipendente), prima alla luce poi
al buio.
La quantità di potassio assorbito y (variabile dipendente) è misurata in
microgrammomolecole per unità di peso di tessuto fogliare.
Dal grafico cartesiano dei dati sperimentali (figura 4)
Figura 4
si evince che una legge del tipo y = at (funzione lineare) si adatta molto bene ai risultati ottenuti in
un dominio T = {t: 0< t  4} e un codominio Ka = {y: 0 y  20}.
Quando l’esperimento è eseguito alla luce (2104 lumen/m2) il coefficiente assume il valore
a = 4 microgrammomolecole per unità di peso per ora.
Al buio il coefficiente a si riduce ad 1.8 microgrammomolecole per unità di peso per ora.
La costante a è detta tasso di assorbimento; la legge della funzione dice che y (quantità di
y
potassio assorbita) è proporzionale a t secondo un fattore a:
a= .
t
51