piano cartesiano 2
y
u
9
8
7
6
5
4
3
2
1
1 2 3 4 5 6
7 8
9
x
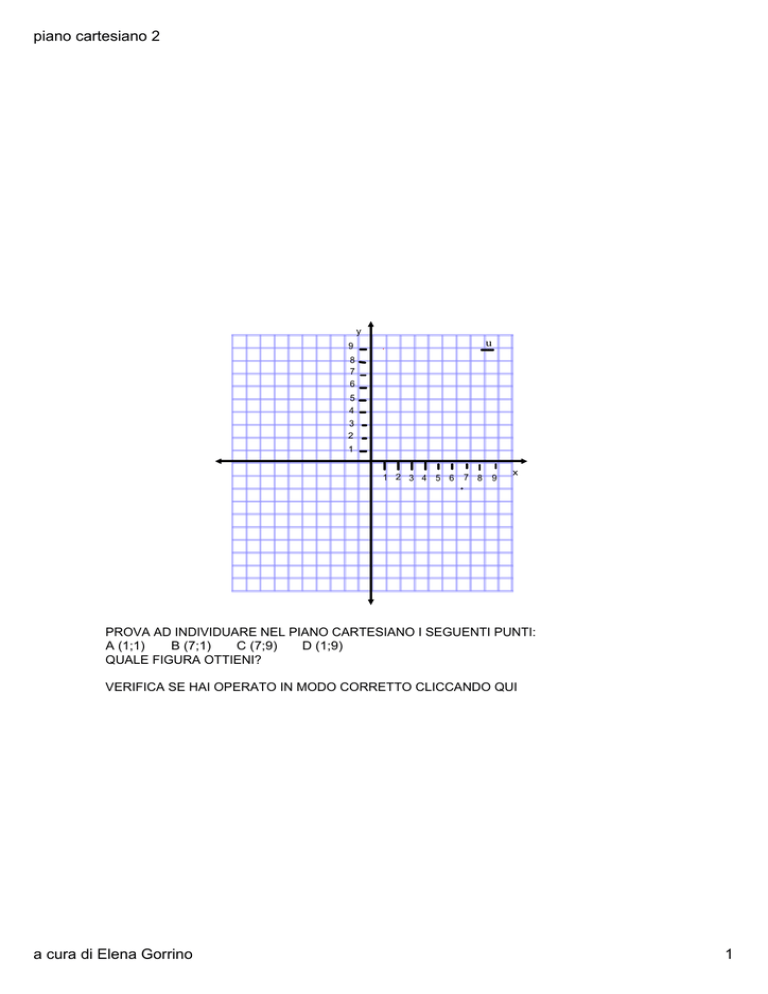
PROVA AD INDIVIDUARE NEL PIANO CARTESIANO I SEGUENTI PUNTI:
D (1;9)
C (7;9)
B (7;1)
A (1;1)
QUALE FIGURA OTTIENI?
VERIFICA SE HAI OPERATO IN MODO CORRETTO CLICCANDO QUI
a cura di Elena Gorrino
1
piano cartesiano 2
y
9
D
C
A
B
8
7
6
5
4
3
2
1
1 2 3 4 5 6 7 8 9
x
Un rettangolo
a cura di Elena Gorrino
2
piano cartesiano 2
y
9
8
7
6
5
4
3
2
1
1 2 3 4 5 6 7 8 9
x
PROVA AD INDIVIDUARE NEL PIANO CARTESIANO I SEGUENTI PUNTI:
D (0;4)
C (4;4)
B (7;0)
A (­3;0)
QUALE FIGURA OTTIENI?
VERIFICA LA CORRETTEZZA CLICCANDO QUI
a cura di Elena Gorrino
3
piano cartesiano 2
y
9
8
7
6
5
4
D
C
3
2
A
1
B
1 2 3 4 5 6 7 8 9
x
Un trapezio isoscele
a cura di Elena Gorrino
4
piano cartesiano 2
LA FUNZIONE y = ax
Ogni funzione matematica si può esprimere con una formula matematica che lega i valori numerici delle due variabili x e y.
La formula matematica attraverso la quale si passa dal valore della x al corrispondente valore della y si chiama equazione della funzione.
Proviamo a disegnare nel piano cartesiano una funzione matematica rappresentata da un' equazione di primo grado, funzione cioè dove la x e la y compaiono solo alla prima potenza e sono quindi monomi di 1° grado.
Questa funzione rappresenta la legge della proporzionalità diretta che è y = kx.
• Una funzione del tipo y = ax è l'equazione di una retta passante per l'origine degli assi.
• Il termine a, il coefficiente della x, è detto coefficiente angolare della retta e ne
caratterizza l'inclinazione rispetto all'asse x. Al variare di a essa rappresenta quindi il fascio di rette di centro O, in particolare:
­ per a > 0 rappresenta le rette del fascio giacenti nel I e III quadrante;
­ per a < 0 rappresenta le rette del fascio giacenti nel II e IV quadrante;
­ per a = 1 rappresenta la retta bisettrice del I e III quadrante;
­ per a = ­1 rappresenta la retta bisettrice del II e IV quadrante;
­ per a = 0 l'equazione diventa y = 0 e rappresenta l'asse delle ascisse.
a cura di Elena Gorrino
5












