Compitino 21 aprile_ 2015

FISICA per SCIENZE BIOLOGICHE A.A. 2014/2015
I Prova in itinere – 21 Aprile 2015
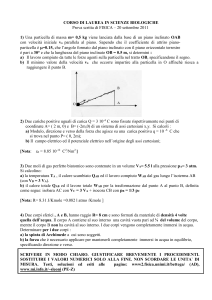
1) CINEMATICA
Un ragazzo corre lungo un sentiero di montagna pianeggiante e rettilineo, con velocità costante, pari
a v0 = 3 m/s. Alla fine di un tratto d = 300 m il ragazzo fa un salto, con velocità parallela al
sentiero, in modo da superare un ruscello, e atterra in un punto a quota h = 1.7 m inferiore, rispetto
la quota del salto. Determinare:
a) il tempo impiegato a percorrere il tratto d rettilineo e l’accelerazione costante a che avrebbe
dovuto avere per percorrere d nello stesso intervallo di tempo, partendo da fermo.
b) Il tempo di volo durante il salto e la distanza orizzontale raggiunta, dopo il salto.
c) Facoltativo: la velocità nel momento di atterraggio, specificandone le componenti, il
modulo e l’angolo di inclinazione rispetto all’orizzontale.
2) DINAMICA Una particella di massa 150 g viene lasciata libera di muoversi alla sommità
(punto O) di un piano liscio, inclinato di un angolo di 60° rispetto al piano orizzontale. Il piano
inclinato (OB) è lungo 2 m. Raggiunta la base del piano inclinato (punto B) prosegue lungo un
piano orizzontale scabro e si arresta dopo un intervallo di tempo di 4 s nel punto C. Si determini :
a) la Reazione normale al piano inclinato e l’accelerazione della particella durante la discesa
lungo il piano inclinato.
b) La velocità nel punto B ed il coefficiente di attrito del piano orizzontale scabro nel tratto BC.
3) LAVORO ed ENERGIA
Una particella di massa m= 200 g viene lasciata libera di muoversi dal punto A della guida mostrata in
figura, dove :
A
B
C
D
E
F
AB è un quarto di circonferenza di raggio 1 m, BC è un tratto verticale di 3 m, CD è un quarto di
circonferenza di raggio 1 m, DE è un tratto orizzontale liscio, EF è una molla di costante elastica k =
300 N/m, inizialmente con lunghezza pari a quella naturale. Si determini:
a) Il Lavoro compiuto dalla forza Peso mentre la particella si sposta da A fino a D e l’energia cinetica della
particella in B e in D.
b) L’accelerazione centripeta della particella nel punto C e la massima compressione della molla quando
viene raggiunta dalla particella.
SCRIVERE IN MODO CHIARO. GIUSTIFICARE I PROCEDIMENTI. SOSTITUIRE I VALORI NUMERICI SOLO ALLA
FINE. NON SCORDARE LE UNITA` DI MISURA. Testi, soluzioni ed esiti alle pagine:
www2.fisica.unimi.it/bettega, www.mi.infn.it/~sleoni
Soluzione Cinematica
a) Nell’ipotesi iniziale di moto rettilineo e uniforme, con velocità costante v0= 3 m/s, il tempo
impiegato è pari a:
t=d/v0 = 300 m/3 m/s = 100 s.
Se il moto fosse rettilineo con accelerazione costante a e velocità iniziale 0 si avrebbe:
d = x0 + v0 t + ½ a t2 = ½ a t2
da cui segue:
a = 2 d/t2 = 2 x 300 m/(100s)2 = 0.06 m/s2
b) Dopo il salto il moto è parabolico, con accelerazione di gravità g e velocità iniziale v0, parallela a
asse x.
Le equazioni del moto in x e y sono:
x(t) = x0 + v0x t = v0 t
y(t) = -h = y0 + v0y t – 1/2g t2 = – 1/2g t2
Dove si è preso un sistema di assi cartesiani (x,y) con asse x e y paralleli e perpendicolari al
suolo e origine nel punto in cui è partito il salto. Il tempo di volo è quindi :
t = (2h/g)1/2 = (2 x 1.7m/9.8 m/s2)1/2 = 0.59 s
La distanza orizzontale percorsa con il salto è quindi :
x = 3 m/s x 0.59 s = 1.77 m
b) facoltativo:
le componenti della velocità nel punto di atterraggio sono date da:
vx = vx0 = 3 m/s
vy = vy0 – gt = -gt = -9.8 m/s2 x 0.59 s = -5.8 m/s
Il modulo è pari a
V = (vx2 + vy2)1/2 = 6.5 m/s
L’angolo di inclinazione è pari a:
q = tg-1 (vy/vx) = -61.4°
Soluzione Dinamica
a) Scelto il sistema d’assi (x,y), con l’asse x parallelo e l’asse y perpendicolare al piano inclinato,
la reazione Normale al piano inclinato è N= mg cos 60°j =0.735 N j (il modulo è uguale alla
componente della forza Peso perpendicolare al piano inclinato). La Forza risultante, parallela al
piano inclinato, è F =mgsen 60°i . L’accelerazione della particella è pertanto a =gsen60°i = 8.48
m/s2i. Il moto della particella è uniformemente accelerato.
b) La velocità nel punto B si può calcolare dalle relazioni per posizione e velocità in funzione del
tempo dei moti rettilinei con accelerazione costante:
x= ½ at2 e v = at , da cui si ricava che il tempo impiegato per arrivare in B è 0.686s e la velocità
in B è 5.81 m/s.
Nel tratto orizzontale scabro la forza Risultante agente è la Forza di attrito F = - mg ì e
l’accelerazione a = - g ì . Si ricava dalla relazione v= at + vB dove v=0 e a= - g . Si
ottiene- 
Soluzione Lavoro ed Energia
a) Il Lavoro compiuto dalla Forza Peso quando la particella si sposta da A fino a D è L= U(A)U(D) = = mghA - mghD dove hA -= 5m e hD =0 . Risulta pertanto L= 9.8 J.
L’energia cinetica della particella in B si calcola applicando il teorema di conservazione
dell’energia meccanica ai punti A e B: mghA = mghB + Ecin B da cui Ecin B = mghA - mghB = 1.96
J.
L’energia cinetica della particella in D si calcola applicando il teorema di conservazione
dell’energia meccanica ai punti A e D: mghA = mghD + EcinD da cui EcinD = mghA - mghD = 9.8 J.
b) L’energia cinetica della particella in C si calcola allo stesso modo e risulta 7.84 J , da cui si
ricava facilmente l’accelerazione centripeta in C, ac = v2C /R = 78.4 m/s2.
La massima compressione della molla si calcola applicando il teorema di conservazione
dell’energia meccanica al sistema molla- particella : ½ x2 = mghA , da cui x = 0.26 m.