CORSO DI LAUREA IN SCIENZE BIOLOGICHE
Prova scritta di FISICA – 27 Gennaio 2015
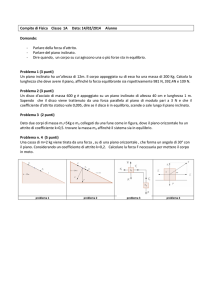
1) Una particella di massa m = 0.5 kg viene lanciata dalla base di un piano inclinato OAB con velocità
iniziale vo, parallela al piano. Sapendo che il coefficiente di attrito piano-particella è = 0.15, che
l'angolo formato dal piano inclinato con il piano orizzontale terrestre è pari a 30° e che la lunghezza del
piano OB = 0.5 m , si determini:
a) il lavoro compiuto da tutte le forze agenti sulla particella nel tratto OB, specificandone il segno.
b) il minimo valore della velocità vo che occorre impartire alla particella in O , affinchè riesca a
raggiungere il punto B .
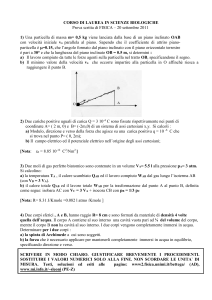
2) Due cariche positive uguali Q pari a 2 10-4 C sono fissate
rispettivamente nei punti A= ( 1m, 0) e B= (-1m,0)
di un sistema di assi cartesiani x,y. Si calcoli :
a) modulo, direzione e verso della forza che agisce su una carica
positiva q = 10 -6 C che si trova nel punto P= ( 0, 1m);
b) il lavoro che le forze del campo compiono quando la carica
q viene spostata da P a R con R= ( 0, 2m).
[N.B. 0 = 8.85 10-12 C2/Nm2 ]
3) Un corpo cubico di lato L = 10 cm è formato da un materiale di densità 5 volte superiore a quella dell’acqua.
Il cubo contiene al suo interno una cavità vuota pari ad 1/5 del volume del corpo. Il cubo viene completamente
immerso in acqua. Determinare:
a) la spinta di Archimede;
b) la forza che è necessario applicare per mantenere il corpo completamente immerso in acqua in equilibrio,
specificandone direzione e verso.
4) Una mole di un gas perfetto monoatomico passa dallo stato iniziale A di coordinate termodinamiche : p A = 2
atmosfere, VA = 10 litri allo stato finale D , attraverso le seguenti trasformazioni:
AB , isobara con VB = 20 litri : BC, isoterma con VC = 40 litri ; CD, isovolumica con pD = 0.5 atmosfere.
a) Si disegnino le tre trasformazioni AB, BC , CD in un diagramma ( V, p) e si calcoli la quantità di calore
totale scambiata nel passaggio del gas dallo stato iniziale A allo stato finale D attraverso le tre trasformazioni
date. Si precisi se la quantità di calore è assorbita o ceduta .
b) Si calcoli la variazione di energia interna del gas nel passaggio dallo stato iniziale A allo stato finale D.
[N.B. R= 8.31 J/Kmole =0.082 l atm /K mol]
SCRIVERE IN MODO CHIARO. GIUSTIFICARE BREVEMENTE I PROCEDIMENTI.
SOSTITUIRE I VALORI NUMERICI SOLO ALLA FINE. NON SCORDARE LE UNITA` DI
MISURA.
Testi, soluzioni ed esiti alle pagine:
www2.fisica.unimi.it/bettega/ (A-L), www.mi.infn.it/~sleoni (M-Z)
SOLUZIONE ESERCIZIO 1 (Meccanica)
a) Scelto un sistema d’assi (x,y) in cui l’asse x è parallelo al piano inclinato e orientato verso l’alto, le
forze agenti sulla particella lanciata lungo il piano inclinato sono: la forza peso, parallela a BA, la reazione
normale al piano inclinato, parallela all’asse y; la forza di attrito, parallela all’asse x e con verso opposto
all’asse x, visto che la particella sale lungo il piano. Durante lo spostamento della particella da O a B,
compiono lavoro diverso da 0, la componente della forza peso parallela al piano inclinato, mgsen 30° (-i ), e
la forza di attrito, mg cos 30° (-i ). Il lavoro compiuta da entrambe è negativo e vale rispettivamente :
LPeso = -mgsen 30° OB e LF attrito = - mg cos 30° OB. Sostituendo i valori numerici si trova rispettivamente :
LPeso = -1,225J e LF attrito = - 0.318 J.
b) Il lavoro compiuto dalla risultante delle forze durante lo spostamento della particella da O a B è
LRis = LPeso + LF attrito = - 1.543 J . Per il teorema Lavoro-Energia cinetica, LRis = Ecin (B) - Ecin (O).
Il minimo valore della velocità con cui occorre lanciare la particella da O, vO , è pertanto quello che soddisfa la
relazione LRis = - Ecin (O) = - ½m (vO ) 2 . Si ricava quindi: vO = 2.48 m/s.
SOLUZIONE ESERCIZIO 2 (Elettrostatica)
2a) La forza elettrostatica F agente sulla carica +q è la somma vettoriale delle forze f A ed f B esercitate dalle
cariche +Q che si trovano rispettivamente in A e in B. Tali forze sono dirette come le congiungenti AP e BP.
La forza F ha componenti: Fx = 0 e Fy = fAy + f By = 2 fAy
Si ha quindi F= Fy j dove Fy = 2 k Q q ( cos 45°) / d 2 (d è la distanza AP) e sostituendo i valori numerici , F=
1.27 j Newton .
2b) Il lavoro L compiuto dalla forza elettrostatica nello spostamento della carica +q da P ad R è uguale alla
differenza dei valori dell’energia potenziale, U , dovuta alle due cariche +Q, in P e in R.
L = U ( P) –U ( R )
U( P ) = 2 kQ q / d U( R ) = 2 kQ q / s dove s è la distanza AR
Sostituendo i valori numerici si ottiene L= 0.94 J .
SOLUZIONE ESERCIZIO 3 (Fluidi)
a) Il modulo della Spinta di Archimede, S A , agente sul corpo immerso totalmente in acqua è pari al peso del
volume di acqua spostata, S A = d H2O V g , dove V è il volume del cubo e d H2O la densità dell’acqua.
Sostituendo i valori numerici si ha S A = 9.8 N. E’ diretta inoltre lungo la verticale terrestre ed è orientata verso
l’alto.
b) La forza F che è necessario applicare per mantenere il corpo completamente immerso in acqua, in equilibrio,
deve equilibrare forza Peso, P, e la Spinta di Archimede, S A . Deve quindi soddisfare la seguente: F+ S A +P =
0. Il modulo della forza Peso è P = d ( V- Vc ) g , dove d è la densità del corpo, con d = 5 d H2O , e Vc è il
volume della cavità, Vc = V/5 . Sostituendo i valori numerici si ha P = 4 S A ed F = 3 S A = 29.4 N.
La forza F è inoltre parallela e concorde in verso alla Spinta Archimedea SA .
SOLUZIONE ESERCIZIO 4 (Termodinamica)
a)
p
A
B
C
D
V
TA = pA VA/ nR = 243.9 K ; TB = pB VB/ nR= 487.8 K
QAB = n cp ( TB - TA ) = 5067.0 J
QBC = LBC = n R TB ln (VC / VB ) = 2809.2 J
TC = TB = 487.8 K ; TD = pD VD/ nR= 243.9 K
QCD = n c V ( TD - TC ) = - 3040.2 J
Qtotale = QAB + QBC + QBC = 4836 J (positiva, quindi assorbita)
b) Poiché A e D hanno la stessa temperatura , la variazione di energia interna è nulla .