1) Un corpo di massa m1= 1 kg di muove su un piano orizzontale

CORSO DI LAUREA IN SCIENZE BIOLOGICHE
Prova scritta di FISICA – 21 luglio 2011
1) Una particella P di massa m = 20 g viene tenuta ferma in un punto O di un piano orizzontale liscio e comprime
di un tratto d = 4 cm una molla di costante elastica k = 1000 N/m, parallela allo stesso piano. Dopo essere stata
lasciata libera di muoversi, la particella P percorre, dal momento in cui si stacca dalla molla, un tratto L = 2m
lungo il piano orizzontale ed urta in modo perfettamente anelastico una seconda particella R di uguale massa m,
inizialmente ferma. Dopo l’urto le due particelle proseguono unite, salendo lungo un piano inclinato di 60°,
scabro con coefficiente di attrito  = 0.1. Si determini:
a) la velocità della particella P immediatamente prima dell’urto con la particella R;
b) la massima quota h del piano inclinato raggiunta dalle due particelle dopo l’urto.
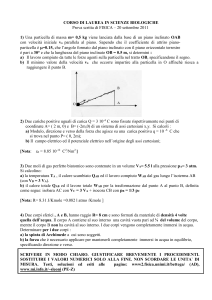
2) Due cariche positive uguali Q pari a 4 10-4 C sono fissate
rispettivamente nei punti A= (-1m, 0) e B= (+1m,0)
di un sistema di assi cartesiani (x,y), come mostrato in figura.
Si calcoli:
a) Modulo, direzione e verso della forza che agisce
su una carica positiva q = 10 -6 C che si trova
nel punto P= (0, 1m);
b) Il lavoro che le forze del campo compiono quando
la carica q viene spostata da P all’origine degli
assi O = (0, 0).
[Note: 0 = 8.85 10-12 C2/Nm2 ]
3) Due moli di un gas perfetto monoatomico compiono, a partire dallo stato iniziale A di coordinate
termodinamiche (pA = 4105 N/m2, VA= 10 cm3), il ciclo reversibile ABCA, in cui AB è una
trasformazione in cui la pressione decresce linearmente all’aumentare del volume, con pB= (1/2) pA
e VB= 4VA ed inoltre BC è una compressione isobara e CA è una compressione isoterma.
a) Si disegni l’intero ciclo in un diagramma (V, p). Si calcolino le coordinate termodinamiche di C
e la variazione di energia interna relativa alla trasformazione AB.
b) Si calcoli la quantità di calore scambiata durante l'intero ciclo.
[Nota: R= 8.31 J/Kmole =0.082 l atmo /Kmole]
4) Un corpo sferico di raggio R= 0.2 m contiene al suo interno una cavità vuota, di forma irregolare, pari a 1/4
del suo volume. Si considerino i due seguenti casi :
a) Il corpo completamente immerso in acqua si trova all’equilibrio : si calcoli la densità del corpo.
b) Si supponga che la densità del corpo,  , sia 0.8 volte quella dell’acqua e che il corpo sia trattenuto sul fondo
di un recipiente alto 2 m, pieno di acqua. Si calcoli la velocità del corpo quando, lasciato libero di muoversi,
raggiunge la superficie libera dell’acqua, senza emergere.
SCRIVERE IN MODO CHIARO. GIUSTIFICARE BREVEMENTE I PROCEDIMENTI. SOSTITUIRE I
VALORI NUMERICI SOLO ALLA FINE. NON SCORDARE LE UNITA` DI MISURA. Testi, soluzioni ed esiti
alle pagine: www2.fisica.unimi.it/bettega/ (AD), www.mi.infn.it/~sleoni (PE-Z)
SOLUZIONE ESERCIZIO 1
(Meccanica)
a) La velocità della particella P immediatamente prima dell’urto con la particella R è uguale alla
velocità di P allo stacco dalla molla poiché il piano è liscio . La velocità di P allo stacco dalla molla
si calcola applicando il teorema di conservazione dell’energia applicato al sistema molla + particella P
all’istante iniziale e a quello dello stacco di P dalla molla. Si ha quindi:
½ k d2 = ½ m v P 2 da cui si ricava v P = 4  5 m/s = 8.94 m/s.
b) Nell’urto tra le due particelle si conserva la quantità di moto del sistema , pertanto la velocità delle
due particelle vP+R dopo l’urto si ricava dalla seguente: mvP = ( m+m) vP+R e risulta
vP+R = 2  5 m/s = 4.47 m/s.
Il tratto D percorso dalle due particelle sul piano inclinato scabro si calcola applicando il teorema
lavoro-energia cinetica, dove compiono lavoro ( negativo) la componente della forza peso P// =
2mgsen60° e la forza di attrito Fa =  2mg cos 60° , entrambe parallele al piano inclinato e opposte allo
spostamento. Tenendo conto che l’energia cinetica finale delle due particelle è nulla si ha quindi :
- (2mgsen60° +  2mg cos 60°) D = - ½ 2m v P+R 2 da cui si ricava D= 1.11 m e pertanto la quota h sul
piano inclinato, pari a D sen60°, é h = 0.96m .
SOLUZIONE ESERCIZIO 2
(Elettrostatica)
a) La forza elettrostatica F agente sulla carica +q è la somma vettoriale delle forze fA ed f B esercitate dalle
cariche +Q che si trovano rispettivamente in A e in B. Tali forze sono dirette come le congiungenti AP e BP.
La forza F ha componenti: Fx = 0 e Fy = fAy + f By = 2 fAy.
Si ha quindi F= Fy j dove
Fy = 2 k Q q ( cos 45°) / d 2
Ove d è la distanza AP. Sostituendo i valori numerici si ottiene:
Fy  2  (9  10 9 ) 
4  10 4  10 6
( 2)
2
2
N  2.55 N
2
La forza F è quindi diretta lungo l’asse y ed è pari a F = 2.55 j N.
b) Il lavoro L compiuto dalla forza elettrostatica nello spostamento della carica +q da P ad O è uguale alla
differenza dei valori dell’energia potenziale U dovuta alle due cariche +Q, tra i punti P e in O.
L = U (P) –U (O)
U(P) = 2 kQ q / d = 5.1 J
U(O) = 2 kQ q / s = 7.2 J
con d pari alla distanza AP che è uguale a BP
con pari alla distanza AO che è uguale BO
Sostituendo i valori numerici si ottiene L = -2.1 J .
SOLUZIONE ESERCIZIO 4
(Fluidi)
a) Il corpo è in equilibrio , con il volume totalmente immerso, pertanto la spinta Archimedea equilibra
la forza Peso : H2O V g =  0.75 V g da cui si ricava  = 1333 kg/m3.
b) In questo caso la risultante delle forze (spinta di Archimede e Peso ) non è nulla e nel tratto percorso
dal corpo dal fondo del recipiente alla superficie dell’acqua (d = 1.60 m, tenendo conto del raggio del
corpo), compie lavoro positivo L che, per il teorema lavoro- energa cinetica, uguaglia la variazione di
energia cinetica del corpo.
Si ha quindi: L = (H2O V g - 0.8 H2O 0.75 V g ) d = Ecin -0 = ½ (0.8 H2O 0.75 V) v2 da cui si ricava
facilmente v = 4.6 m/s .
SOLUZIONE ESERCIZIO 3
(Termodinamica)
a) Le variabili termodinamiche (p,V,T) per lo stato C possono essere ricavate applicando l’equazione
di stato dei gas perfetti
pV  nRT
p
A
sapendo che:
pA= 4105 N/m2, VA= 10 x (102)3 m3 = 10-5 m3;
pB= 2105 N/m2, VB= 410-5 m3;
C
pC= pB=2105 N/m2 (essendo BC isobara)
pCVC= pAVA (essendo AC isoterma) , da cui
VC = pAVA / pC = 2105 m3
Inoltre:
TA = TC = pAVA/nR = (4105 N/m2) (105 m3) / (2 moli 8.31 J/K mole) = 0.24 K
La variazione di energia interna U nella trasformazione AB è :
U= n cV T= n cV (TB TA)= n (3R/2)( pB VB  pA VA)/ nR= 6 J
b) La quantità di calore scambiata nell’intero ciclo Qciclo è:
Qciclo = Lciclo = LAB +LBC+ LCA
LAB = (pA+ pB)( VB  VA )/2 = 9 J
LBC= pB ( VC  VB )= 4 J
LCA=  p dV = nRTA ln (VA / VC ) = 2.77 J
Qciclo = 2.24 J
B
V