FORMULE DI ADDIZIONE
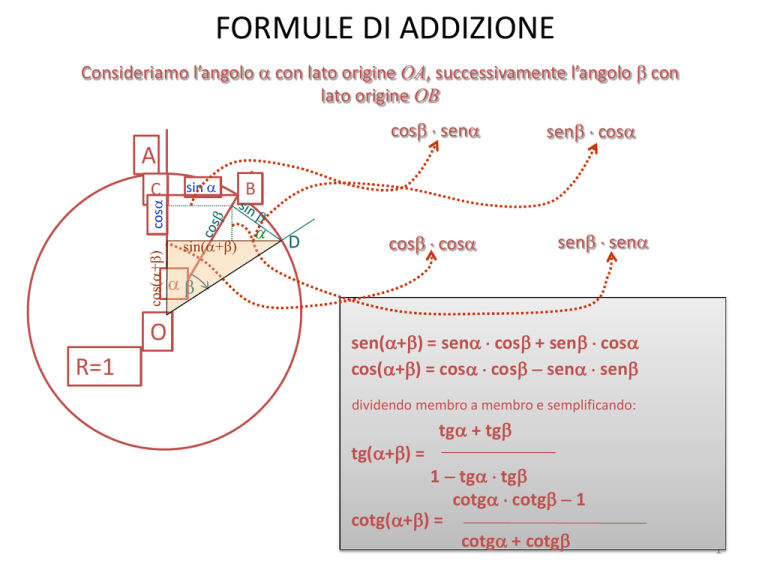
Consideriamo l’angolo con lato origine OA, successivamente l’angolo con
lato origine OB
cos sen
sen cos
A
sin
cos(+)
cos
C
O
R=1
sin(+)
B
D
cos cos
sen sen
sen(+) = sen cos + sen cos
cos(+) = cos cos sen sen
dividendo membro a membro e semplificando:
tg + tg
tg(+) =
1 tg tg
cotg cotg 1
cotg(+) =
cotg + cotg
1
FORMULE DI SOTTRAZIONE
Sostituendo nelle formule di addizione all’angolo l’angolo , si ottiene:
sen() = sen cos sen cos
cos() = cos cos + sen sen
tg tg
tg() =
1+ tg tg
cotg cotg 1
cotg() =
cotg + cotg
FORMULE DI DUPLICAZIONE
Ponendo nelle formule di addizione = , si ottiene:
sen(2) = 2 sen cos
cos(2) = cos2 sen2
2tg
tg(2) =
1 tg2
cotg2 1
cotg(2) =
2cotg
2
FORMULE DI BISEZIONE
Consideriamo il sistema composto dall’equazione fondamentale e dalla formula di duplicazione
del coseno:
1 = sen2 + cos2
cos 2 = cos2 sen2
sottraendo la seconda dalla prima:
1 cos2 = 2sen2
ponendo /2 al posto di :
1 cos = 2sen2(/2)
evidenziando sen(/2):
1 cos
sin
2
2
sommando la seconda alla prima:
cos
dividendo membro a membro:
2
1 cos
2
1 cos
tg
2
1 cos
3
LE TRE ALTEZZE
Le tre altezze si intersecano in un punto H chiamato ortocentro.
A
b
hc
C
H
ha
c
hb
B
a
Considerando i triangoli retti definiti dalle
tre altezze ha, hb, hc, si può scrivere:
ha = b sen = c sen
hb = c sen = a sen
hc = b sen = a sen
4
LE TRE MEDIANE
Le tre mediane si intersecano in un punto G, detto baricentro del triangolo.
b
-2
A
b
-2
c
-2
mc
ma
G
mb
c
-2
a
-2
’
M
C
a
-2
’=200C-
Consideriamo i due triangoli ABM e AMC
a2
c2 = ---- + ma2 - a ma cos
4
a2
b2 = ---- + ma2 + a ma cos
4
Sommando membro a membro:
a2
b2 + c2 = ---- + 2 ma2
2
B
Il baricentro G si trova a una distanza
dal vertice
pari ai 2/3
della mediana, e a 1/3 della mediana
dal punto medio del lato opposto
AG = 2/3 ma - GM = 1/3 ma
1
ma = ---- 2b2 + 2c2 – a2
2
1
mb = ---- 2a2 + 2c2 – b2
2
1
mc = ---- 2b2 + 2a2 – c2
2
5
LE TRE BISETTRICI
Le tre bisettrici si intersecano in un punto O, centro del cerchio inscritto.
Consideriamo l’area del triangolo ABC, ottenuta
come somma di quelle dei due triangoli ABN e ANC
b
A
C
1
bc sen = --- cn sen ---- + --- bn sen ---2
2
2
2
2
Applicando la f. di duplicazione del seno al 1° membro:
1
1
O
nb
c
1
---
nc
na
1
bc sen --- cos --- = --- cn sen ---- + --- bn sen ---2
2
2
2
2
2
N
a
Dividendo per sen(/2):
1
1
1
bc cos --- = --- cn + --- bn = --- n (b + c)
2
2
2
2
B
2bc
n = ------------ cos --c+b
2
2ac
n = ------------ cos --a+c
2
2ab
n = ------------ cos --a+b
2
6
LA RETTA DI EULERO
In un triangolo i seguenti punti sono allineati:
baricentro G (intersezione delle tre mediane),
ortocentro H (intersezione delle tre altezze),
circocentro O (intersezione degli assi dei tre lati).
La retta che li congiunge viene detta retta di Eulero.
A
b
C
H
G
c
O
a
B
7