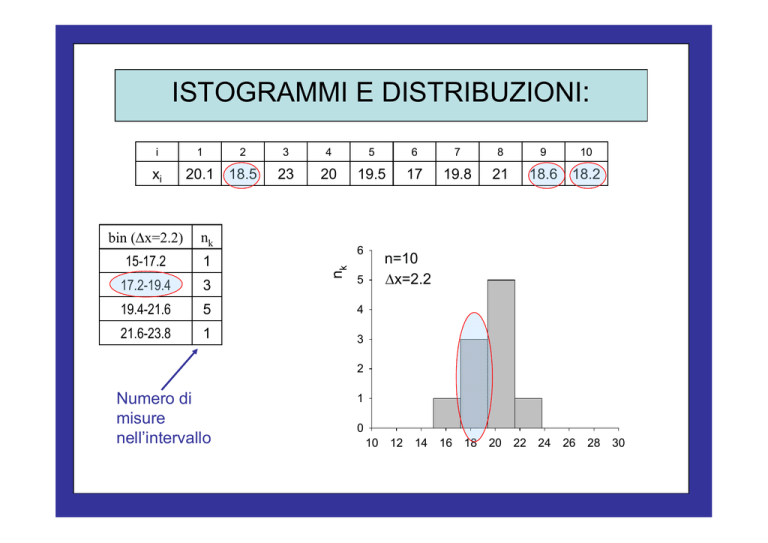
ISTOGRAMMI E DISTRIBUZIONI:
i
xi
1
2
20.1 18.5
3
4
5
6
7
8
23
20
19.5
17
19.8
21
bin (x=2.2)
nk
15-17.2
1
17.2-19.4
3
19.4-21.6
5
4
21.6-23.8
1
3
nk
6
9
10
18.6 18.2
n=10
x=2.2
5
2
Numero di
misure
nell’intervallo
1
0
10
12
14
16
18
20
22
24
26
28
30
ISTOGRAMMI E DISTRIBUZIONI:
xi
1
2
20.1 18.5
3
4
5
6
7
8
23
20
19.5
17
19.8
21
bin (x=2.2)
nk
Fk= nk/N
15-17.2
1
0.1
17.2-19.4
3
0.3
19.4-21.6
5
0.5
21.6-23.8
1
0.1
0.6
Fk
i
9
10
18.6 18.2
n=10
x=2.2
0.5
0.4
0.3
0.2
Numero di Frequenza
misure
nell’intervallo
0.1
0.0
10
12
14
16
18
20
22
24
26
28
30
ISTOGRAMMI E DISTRIBUZIONI:
xi
1
2
20.1 18.5
3
4
5
6
7
8
23
20
19.5
17
19.8
21
bin (x=2.2)
nk
Fk= nk/N
Fk/x
15-17.2
1
0.1
0.045
17.2-19.4
3
0.3
0.136
19.4-21.6
5
0.5
0.227
21.6-23.8
1
0.1
0.045
Fk/x
i
0.30
9
10
18.6 18.2
n=10
x=2.2
0.25
0.20
0.15
0.10
Numero di Frequenza
Densità di
misure
frequenza
nell’intervallo
0.05
0.00
10
12
14
16
18
20
22
24
26
28
30
Fk/x
ISTOGRAMMI E DISTRIBUZIONI:
0.30
0.30
n=10
x=2.2
0.25
n=100
x=1
0.25
0.20
0.20
0.15
0.15
0.10
0.10
0.05
0.05
0.00
0.00
10
12
14
16
18
20
22
24
26
0.30
28
30
10
12
14
16
22
24
26
28
18
n=1000
x=0.5
0.25
0.20
0.15
0.10
0.05
0.00
10
12
14
16
18
20
30
20
22
24
26
28
30
LA DISTRIBUZIONE GAUSSIANA:
Funzione densità di
probabilità:
gaussiana:
f ( x)
1
2
e
x 2
2 2
Funzione della varabile x caratterizzata da due parametri: e
f(x)
x
x
f ( x) 0
f MAX ( x)
f ( x) dx 1
x
1
2
LA DISTRIBUZIONE GAUSSIANA:
0.25
0.2
0.15
u=10; sigma=2
0.1
0.05
0
0
5
10
15
20
25
30
Al variare di varia la posizione della curva (traslazione lungo l’asse x)
LA DISTRIBUZIONE GAUSSIANA:
0.25
0.2
0.15
u=10; sigma=2
u=15; sigma=2
0.1
0.05
0
0
5
10
15
20
25
30
Al variare di varia la posizione della curva (traslazione lungo l’asse x)
LA DISTRIBUZIONE GAUSSIANA:
0.25
0.2
u=10; sigma=2
0.15
u=15; sigma=2
0.1
u=20; sigma=2
0.05
0
0
5
10
15
20
25
30
Al variare di varia la posizione della curva (traslazione lungo l’asse x)
LA DISTRIBUZIONE GAUSSIANA:
0.25
0.2
0.15
u=10; sigma=2
0.1
0.05
0
0
5
10
15
Al variare di varia la larghezza della curva
20
LA DISTRIBUZIONE GAUSSIANA:
0.25
0.2
0.15
u=10; sigma=2
u=10; sigma=3
0.1
0.05
0
0
5
10
15
Al variare di varia la larghezza della curva
20
LA DISTRIBUZIONE GAUSSIANA:
0.25
0.2
0.15
u=10; sigma=2
u=10; sigma=3
u=10; sigma=5
0.1
0.05
0
0
5
10
15
Al variare di varia la larghezza della curva
20
LA DISTRIBUZIONE GAUSSIANA:
Significato della gaussiana nel caso di misure affette solo da errori casuali:
corrisponde al valore vero che si vuole misurare
è legata alla precisione sulla misura: minore è la larghezza
della curva, migliore è la precisione della misura
x1 x2 x3 ...x N
N x
i 1 i
N
N
N x
x
Nell’ipotetico caso di un numero infinito di misure il
valor medio risulta uguale al valore vero . Nel
caso reale di un numero finito di misure, il valor
medio è la miglior stima del valore vero.
N
Sx
2
(
x
x
)
i
i 1
N
( N 1)
Sx
Nell’ipotetico caso di un numero infinito di misure
la deviazione standard risulta uguale al parametro
. Nel caso reale di un numero finito di misure, la
deviazione standard è la miglior stima di .
LA DISTRIBUZIONE GAUSSIANA:
Significato della gaussiana nel caso di misure affette solo da errori casuali:
a ciascun area sottesa dalla curva corrisponde un valore di probabilità
L’area tratteggiata fornisce
la probabilità di ottenere da
una misura un valore che
dista dal valore medio non
più di una deviazione
standard.
0.25
=10 ; =2
0.20
0.15
x2=
x
0.10
0.05
0.00
2
4
6
8
10
12
14
16
18
Tale area è pari a circa
0.68. Quindi nel 68% dei
casi, ci aspettiamo di trovare
come risultato della misura
un valore che dista meno di
una deviazione standard dal
valore vero
LA DISTRIBUZIONE GAUSSIANA:
Significato della gaussiana nel caso di misure affette solo da errori casuali:
a ciascun area sottesa dalla curva corrisponde un valore di probabilità
0.25
=10 ; =2
0.20
0.15
x2=
x
0.10
0.05
0.00
2
4
6
8
10
12
14
16
18
L’area tratteggiata fornisce
la probabilità di ottenere da
una misura un valore che
dista dal valore medio non
più di due deviazioni
standard.
Tale area è pari a circa
0.95. La probabilità di
trovare il risultato della
misura nell’intervallo ±2σ dal
valore vero è quindi pari a
circa il 95%.
LA DISTRIBUZIONE GAUSSIANA:
Significato della gaussiana nel caso di misure affette solo da errori casuali:
a ciascun area sottesa dalla curva corrisponde un valore di probabilità
0.25
=10 ; =2
È possibile ricavare tale
probabilità per qualsiasi
intervallo, simmetrico
o meno, utilizzando una
tabella che fornisce le
probabilità di trovare un
valore in un generico
intervallo simmetrico ±tσ
centrato intorno al valore
vero μ.
t=
0.20
0.15
x2=t
x1=t
0.10
0.05
0.00
2
4
6
8
10
12
14
16
18
LA TABELLA DELLA GAUSSIANA:
0.25
0.20
0.15
t
0.10
t
t( x)
0.05
0.00
2
4
6
8
10
12
14
16
18
x
LA TABELLA DELLA GAUSSIANA:
Esercizi
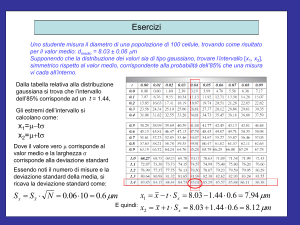
Uno studente misura il diametro di una popolazione di 100 cellule, trovando come risultato
per il valor medio: dmedio = 8.03 ± 0.06 m
Supponendo che la distribuzione dei valori sia di tipo gaussiano, trovare l’intervallo [x1, x2],
simmetrico rispetto al valor medio, corrispondente alla probabilità dell’85% che una misura
vi cada all’interno.
Dalla tabella relativa alla distribuzione
gaussiana si trova che l’intervallo
dell’85% corrisponde ad un t = 1.44,
Gli estremi dell’intervallo si
calcolano come:
x1=t
x2=t
Dove il valore vero corrisponde al
valor medio e la larghezza
corrisponde alla deviazione standard
Essendo noti il numero di misure e la
deviazione standard della media, si
ricava la deviazione standard come:
S x S x N 0.06 10 0.6
E quindi:
x1 x t S x 8.03 1.44 0.6 7.17
x2 x t S x 8.03 1.44 0.6 8.89
Esercizi
In un allevamento ci sono 23000 pecore il cui peso medio è di 45.5 ± 0.05 kg.
Se i pesi degli ovini sono distribuiti secondo una curva gaussiana, dare il numero N1 dei capi con
peso compreso tra 43 e 48 kg e il numero N2 dei capi con peso inferiore a 55 kg
La distribuzione del peso degli ovini è centrata sul valore medio 45.5 con deviazione standard pari a:
S x S x N 0.05 23000 7.6
Per il calcolo di N1 si ha a che fare con un intervallo simmetrico [43-48] rispetto al valore medio 45.5.
Per il calcolo della probabilità associata a tale intervallo si ricava dapprima il valore di t e poi si
guarda la tabella della gaussiana:
x1 x t S x
x2 x t S x
45.5 43
0.33
7 .6
48 45.5
48 45.5 t 7.6 t
0.33
7. 6
43 45.5 t 7.6 t
Vi è quindi una probabilità del 25.86% che le pecore
abbiano un peso tra 43 e 48 kg. Essendo le pecore totali
23000 ne consegue che:
N1 23000
25.86
5948
100
(segue)
Esercizi
In un allevamento ci sono 23000 pecore il cui peso medio è di 45.5 ± 0.05 kg.
Se i pesi degli ovini sono distribuiti secondo una curva gaussiana, dare il numero N1 dei capi con
peso compreso tra 43 e 48 kg e il numero N2 dei capi con peso inferiore a 55 kg
Per il calcolo di N2 si ha a che fare con un intervallo NON simmetrico. Il numero di ovini con peso
inferiore a 55 kg si trova andando a determinare dapprima il valore di t corrispondente a 55:
t
55 45.5
1.25
7.6
Dalla tabella della gaussiana, si trova che P(t=1.25) = 78.37% e corrisponde
all’a probabilità di avere ovini con peso compreso tra 36 e 55 kg
0.06
0.06
0.05
0.05
0.04
0.04
0.03
0.03
0.02
0.02
0.01
0.01
0.00
15 20 25 30 35 40 45 50 55 60 65 70 75
0.00
15 20 25 30 35 40 45 50 55 60 65 70 75
Devo tuttavia considerare anche tutti gli ovini con peso inferiore ai 36 kg (coda a sinistra della curva).
(segue)
Esercizi
In un allevamento ci sono 23000 pecore il cui peso medio è di 45.5 ± 0.05 kg.
Se i pesi degli ovini sono distribuiti secondo una curva gaussiana, dare il numero N1 dei capi con
peso compreso tra 43 e 48 kg e il numero N2 dei capi con peso inferiore a 55 kg
E’ sufficiente ricordarsi che l’area totale sottesa dalla gaussiana corrisponde al 100%
0.06
0.05
100 78.37
%
2
0.04
0.03
78.37%
La probabilità di avere un peso inferiore a
55 kg è quindi pari a :
P peso 55kg 50
Da cui il numero di pecore: :
0.02
N1 23000
0.01
0.00
15 20 25 30 35 40 45 50 55 60 65 70 75
78.37
89.185%
2
89.185
20513
100
Esercizi
Una grandezza è distribuita normalmente attorno al valore 30 con deviazione standard pari a 3.
Quale è la percentuale di misure che ci aspetta essere comprese tra 31 e 33?
L’intervallo considerato è un intervallo non simmetrico in cui entrambi gli estremi si trovano a destra
del valore centrale della distribuzione:
x1=t1
x2=t2
Sostituendo i valori degli estremi x1 e x2, del valore medio e della deviazione
standard si ricavano i due valori di t :
31 30
0.33
3
33 30
t2
1
3
t1
Dalla tabella della gaussiana si trova:
P(t1)= 25.86 % (figura A) e P(t2)=68.27 % (figura B)
(segue)
Esercizi
Una grandezza è distribuita normalmente attorno al valore 30 con deviazione standard pari a 3.
Quale è la percentuale di misure che ci aspetta essere comprese tra 31 e 33?
Guardando le curve la probabilità associata all’intervallo non simmetrico si ricava come:
P31 x 33
P(t 2 ) P(t1 )
21.2%
2
2
Esercizi
Sia data una distribuzione centrata intorno a 25 con larghezza sigma 1.3. Trovare:
(a) l’intervallo corrispondente alla probabilità del 68.27%;
(b) La probabilità di trovare un valore compreso tra 21.9 e 25.5.
a) La probabilità del 68.27% corrisponde all’intervallo: []
Quindi:
0.35
0.30
25 1.3 23.7
25 1.3 26.3
0.25
0.20
0.15
b) L’intervallo è non simmetrico.
Calcolo i valori di t relativi ai due estremi:
25 21.9
2.38
1 .3
25.5 25
t2
0.385
1 .3
0.10
0.05
0.00
t1
Dalla tabella della gaussiana:
P(t1)= 98.27 %
P(t2)= 30 %
(segue)
20
21
22
23
24
25
26
27
28
29
26
27
28
29
30
0.35
0.35
0.30
0.30
P(t1)
0.25
0.25
0.20
0.20
0.15
0.15
0.10
0.10
0.05
0.05
0.00
20
21
22
23
24
25
26
27
28
29
30
P(t2)
0.00
20
21
22
23
24
25
30
Esercizi
Sia data una distribuzione centrata intorno a 25 con larghezza sigma 1.3. Trovare:
(a) l’intervallo corrispondente alla probabilità del 68.27%;
(b) La probabilità di trovare un valore compreso tra 21.9 e 25.5.
0.35
0.35
0.30
0.30
P(t1) /2
0.25
P(t2) /2
0.25
0.20
0.20
0.15
0.15
0.10
0.10
0.05
0.05
0.00
20
21
22
23
24
25
26
27
28
29
30
0.00
20
21
22
Osservando le aree e sfruttando la simmetria della curva si trova:
P21.9 x 25.5
P(t1 ) P(t 2 )
64%
2
2
23
24
25
26
27
28
29
30