Distribuzione Gaussiana
Fra le densità di probabilità continue, la più
importante è la densità di probabilità normale, detta
anche distribuzione di Gauss, in onore del matematico
Carl Friedrich Gauss (1777-1855)
Essa è anche nota come legge degli errori, perché
descrive la distribuzione degli errori casuali relativi a
successive misure di una quantità fisica; inoltre
diversi
fenomeni
continui
seguono
approssimativamente una distribuzione normale.
Distribuzione Gaussiana
La densità di probabilità normale è definita dalla
funzione
2
1
f ( x) =
e
σ 2π
1 x−µ
−
2 σ
−∞ < x < ∞
,
di parametri µ e σ , con σ > 0
E’ definita su tutto l'asse reale ed è positiva; è simmetrica
ed il suo massimo, assunto nel punto di ascissa µ, vale
y max =
1
σ 2π
Grafico della distribuzione Gaussiana
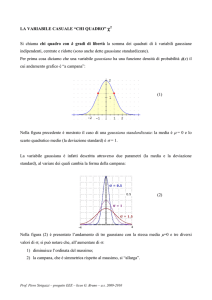
La distribuzione normale
ha una forma a campana,
il cui grafico di è del tipo
illustrato nella figura 1
µ=2
0.8
Nella figura 2 si riportano i
grafici della distribuzione
normale per un dato valore
di µ e per diversi valori di
σ:
σ = 0.5
0.6
0.4
σ=1
0.2
σ=2
0
-2
-1
0
1
2
3
4
5
6
Grafico della distribuzione Gaussiana
Nella figura 3 si riportano i grafici della distribuzione
normale per un dato valore di σ e per diversi valori di µ
0.4
σ=1
0.3
µ=3
0.2
µ=2
0.1
µ=1
0
-2
-1
0
1
2
3
4
5
6
Funzione di ripartizione normale
La funzione di distribuzione o funzione di ripartizione
normale è data da
2
1 t −µ
1 x − 2 σ
F ( x) = P( X ≤ x) =
e
dt , − ∞ < x < ∞
∫
σ 2π −∞
Nella figura il
grafico della
funzione di
distribuzione per
µ = 2 e σ =1
1
0 .8
0 .6
0 .4
0 .2
0
-2
-1
0
1
2
3
4
5
6
Distribuzione Gaussiana standardizzata
La distribuzione normale è una famiglia di
distribuzioni distinte in base ai valori di µ e σ. La
curva più importante è la distribuzione normale
standardizzata. Per ricavarla si passa alla nuova
variabile aleatoria Z, detta variabile standardizzata,
ponendo:
X −µ
Z=
σ
Distribuzione di
probabilità della
variabile normale
standardizzata Z
z2
−
2
1
f (z) =
e ,
2π
−∞ < z < ∞
Distribuzione Gaussiana standardizzata
Nei grafici della distribuzione normale standardizzata
abbiamo le aree comprese rispettivamente tra −1 e 1,
tra −2 e 2 e tra −3 e 3, pari al 68.27%, al 95.44% e al
99.73% dell'area totale, che è 1.
P(-3<Z<3) = 99.7%
P(-1<Z<1) = 68.3%
0.4
0.4
P(-2<Z<2) = 95.4%
0.3
f(z)
0.3
f(z)
0.4
0.2
0.2
0.3
0.1
0.1
f(z)
0.2
0
-4
-3
-2
-1
0
1
2
3
0
-4
4
z
-2
-1
0
z
0.1
0
-4
-3
-3
-2
-1
0
z
1
2
3
4
1
2
3
4