Distribuzioni di
probabilità nel
continuo
Prof.ssa Fabbri Francesca
Classe 5C
Variabili casuali continue
Introduzione:
Una Variabile Casuale o Aleatoria è una grandezza che, nel corso di un esperimento
aleatorio, può assumere valori non noti a priori.
E1, E2,…, En
Se X assume tutti i valori di un intervallo [a;b], allora X è una Variabile Casuale (o
Aleatoria) Continua.
Esempi:
1.
le altezze o i pesi di un gruppo di persone;
2.
i diametri delle sfere di un cuscinetto;
3.
le lunghezze delle viti;
4.
la durata di un tipo di lampadine;
5.
il tempo impiegato a svolgere una certa attività (si dice spesso “il tempo varia
con continuità”…)…
Funzione densità di
probabilità
Osservazione:
Per le Variabili Casuali Continue non ha senso calcolare la
probabilità che X assuma un particolare valore x0 di X ma
piuttosto ci si concentra sulla probabilità che X assuma valori
compresi fra x1 e x2, dove x1 , x2 ∈[ a;b ] ⊂ !
Per il calcolo si usa allora di funzione di densità di probabilità
f(x) che è definita come segue:
(la funzione, non negativa, racchiude con l’asse delle x un’area uguale a 1)
Funzione densità di
probabilità
Con le condizioni indicate in
definizione, la probabilità che
X assuma valori compresi fra
x1 e x2 è allora:
P ( x1 ≤ X ≤ x2 ) = ∫ f ( x )dx
x2
x1
Se l’intervallo [a;b] è finito, si ha:
f ( x ) = 0, per x < a ∨ x > b
così l’area coincide con quella
relativa all’intervallo [a;b].
Il valore della probabilità è
uguale all’area compresa fra
il grafico di f(x) e l’asse delle
ascisse nell’intervallo [x1;x2].
Funzione di ripartizione
Analogamente al caso delle V. C. Discrete, si può parlare di:
1. F(x) è uguale all’area compresa fra il grafico
della funzione di densità f(x) e l’asse delle
ascisse in (-inf;x];
2. F(x) è una primitiva di f(x): F ′(x) = f (x)
3. si ha: P x ≤ X ≤ x = F x − F x
(
1
2
)
( 2)
( 1)
Valore atteso e Varianza di V.C.C.
M (X) = ∫
+∞
−∞
+∞
x ⋅ f ( x ) dx
( )
var ( X ) = ∫ [ x − M(X)] ⋅ f ( x ) dx = M X 2 − ⎡⎣ M ( X )⎤⎦
−∞
2
2
Esempio risolto
Se una V.C.C. varia in [0;2] con funzione densità di probabilità:
⎧ x3
⎪
f (x) = ⎨ 4
⎪0
⎩
se 0 ≤ x ≤ 2
se x < 0 ∨ x > 2
Verificare che sia veramente una funzione di densità:
• f(x)>=0 per ogni x appartenente
all’intervallo [0;2] à ok
2
⎡ x4 ⎤
• Inoltre 2 x 3
à ok
∫
0
4
La funzione di ripartizione è:
dx = ⎢ ⎥ = 1
⎣ 16 ⎦ 0
+∞
2
−∞
0
M ( X ) = ∫ x ⋅ f ( x ) dx = ∫ x ⋅
x3
8
dx = ... =
4
5
2
2
2
x3 ⎛ 8 ⎞
8
oppure = M(X )− [ M(X)] = ∫ x ⋅ dx − ⎜ ⎟ = ...=
0
4 ⎝ 5⎠
75
2
2
2
2
∫
2
3
8
⎛ 8⎞ x
var ( X ) = ∫ [ x − M(X)] ⋅ f ( x ) dx = ∫ ⎜ x − ⎟ ⋅ dx = ...=
−∞
0⎝
5⎠ 4
75
+∞
se x < 0
⎧0
⎪ x 3
x4
⎪ t
F(x) = ⎨
dt =
se 0 ≤ x ≤ 2
16
⎪ 0 4
1
se x > 2
⎪
⎩
Se si chiede, ad es:
x3
dx = ... = 0,25
1
4
⎡ x4 ⎤
oppure = F(1,5) − F(1) = ⎢ ⎥ = ... = 0,25
⎣ 16 ⎦
P (1 ≤ X ≤ 1,5 ) = ∫
1,5
Distribuzione uniforme
continua
Vale:
P ( x1 ≤ X ≤ x2 ) = ∫
Si dimostra che:
+∞
M ( X ) = ∫ x ⋅ f ( x ) dx =
−∞
x2
x1
1
x −x
dx = 2 1
b−a
b−a
a+b
2
2
b − a)
(
var ( X ) = ∫ [ x − M(X)] ⋅ f ( x ) dx =
−∞
+∞
2
La funzione di ripartizione è:
se x < a
⎧0
⎪
⎪x − a
F(x) = ⎨
se a ≤ x ≤ b
⎪b − a
se x > b
⎪
⎩1
12
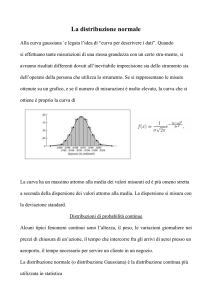
Distribuzione normale o
gaussiana
Fra tutte le funzioni di densità di probabilità, quella normale è fra le più
importanti perché approssima in modo soddisfacente tutte le situazioni in cui la
maggior parte dei valori di X si concentra attorno ad uno particolare.
(
N µ; σ 2
)
indica una V.C. Normale dove i parametri
e
indicano il valor medio e la
deviazione standard della variabile
casuale.
Distribuzione normale o
gaussiana
La curva che rappresenta la
funzione gaussiana è nota
come curva degli errori
accidentali o curva a
campana
• è simmetrica rispetto
alla retta x= ;
• ha un massimo in M ⎛⎜ µ; 1 ⎞⎟
⎝ σ 2π ⎠
• l’asse delle ascisse è
asintoto orizzontale;
• ha due flessi in
corrispondenza di
µ −σ;µ +σ
Distribuzione normale o
gaussiana
A parità di valore medio
ma diversi , si osserva
che si ha:
•
basso è curva
“appuntita” (ossia i
valori di X si avvicinano
in gran parte al valore
medio )
•
alto è curva
“appiattita” (ossia i
valori di X sono piuttosto
distribuiti rispetto al
valore medio )
Distribuzione normale
standardizzata
Per il calcolo dei valori di
probabilità ci si riconduce
sempre però alla normale
standardizzata che ha
valore medio = 0 e
deviazione standard =1
N(0;1)
Essa corrisponde alla
funzione gaussiana 2
1 − z2
f (z) =
e
2π
dove z = x − µ
σ
ossia si “standarizza” la
variabile casuale X nella
variabile casuale Z = X − µ
σ
Distribuzione normale o
gaussiana
N.B.
I valori della funzione di ripartizione della normale standardizzata
sono calcolati in apposite tabelle (Tavole di Sheppard) che
consentono di determinare qualsiasi valore di probabilità abbastanza
agevolmente, altrimenti si usano dei software matematici per risolvere gli
integrali coinvolti.
Tali tabelle forniscono il valore delle aree sottostanti la curva f(z) in
un particolare intervallo; quella del nostro testo, per l’intervallo
[0;z], quindi
F(z) = P(0 < Z < z)
altre per l’intervallo
]−∞;z[
per cui
F(z) = P(−∞ < Z < z)
La parte annerita rappresenta l’area sottostante la distribuzione normale standardizzata dalla media aritmetica a z.
z
0,00
0,01
0,02
0,03
0,04
0,05
0,06
0,07
0,08
0,09
0,0
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
1,0
1,1
1,2
1,3
1,4
1,5
1,6
1,7
1,8
1.9
2,0
2,1
2,2
2,3
2,4
2,5
2,6
2,7
2,8
2,9
3,0
3,1
3,2
3,3
3,4
3,5
3,6
3,7
3,8
3,9
00000
03983
07926
11791
15542
19146
22575
25804
28814
31594
34134
36433
38493
40320
41924
43319
44520
45543
46407
47128
47725
48214
48610
48928
49180
49379
49534
49653
49745
49813
49865
49903
49931
49952
49966
49977
49984
49989
49993
49995
00399
04380
08317
12172
15910
19497
22907
26115
29103
31859
34375
36650
38686
40490
42073
43448
44630
45637
46485
47193
47778
48257
48645
48956
49202
49396
49547
49664
49752
49819
49869
49906
49934
49953
49968
49978
49985
49990
49993
49995
00792
04776
08706
12552
16276
19847
23237
26424
29389
32121
34614
36864
38877
40658
42220
43574
44738
45728
46562
47257
47831
48300
48679
48983
49224
49413
49560
49674
49760
49825
49874
49910
49936
49955
49969
49978
49985
49990
49993
49995
01197
05172
09095
12930
16640
20194
23565
26730
29673
32381
34849
37076
39065
40824
42364
43699
44845
45818
46637
47320
47882
48341
48713
49010
49245
49430
49573
49683
49767
49831
49878
49913
49938
49957
49970
49979
49986
49990
49994
49996
01595
05567
09483
13307
17003
20540
23891
27035
29955
32639
35083
37286
39251
40988
42507
43822
44950
45907
46712
47381
47932
48382
48745
49036
49266
49446
49585
49693
49774
49836
49882
49916
49940
49958
49971
49980
49986
49991
49994
49996
01994
05962
09871
13683
17364
20884
24215
27337
30234
32';94
35314
37493
39435
41149
42647
43943
45053
45994
46784
47441
47982
48422
48778
49061
49286
49461
49598
49702
49781
49841
49886
49918
49942
49960
49972
49981
49987
49991
49994
49996
02392
06356
10257
14058
17724
21226
24537
27637
30511
33147
35543
37698
39617
41309
42786
44062
45154
46080
46856
47500
48030
48461
48809
49086
49305
49477
49609
49711
49788
49846
49889
49921
49944
49961
49973
49981
49987
49991
49994
49996
02790
06749
10642
14431
18082
21566
24857
27935
30785
33398
35769
37900
39796
41466
42922
44179
45254
46164
46926
47558
48077
48500
48840
49111
49324
49492
49621
49720
49795
49851
49893
49924
49946
49962
49974
49982
49988
49992
49995
49996
03188
07142
11026
14803
18439
21904
25175
28230
31057
33646
35993
38100
39973
41621
43056
44295
45352
46246
46995
47615
48124
48537
48870
49134
49343
49506
49632
49728
49801
49856
49897
49926
49948
49964
49975
49983
49988
49992
49995
49997
03586
07535
11409
15173
18793
22240
25490
28524
31327
33891
36214
38298
40147
41774
43189
44408
45449
46327
47062
47670
48169
48574
48899
49158
49361
49520
49643
49736
49807
49861
49900
49929
49950
49965
49976
49983
49989
49992
49995
49997
Come si legge la
Tavola di Sheppard
N.B.
La stessa tavola di Sheppard,
data la simmetria della curva
gaussiana, può essere usata
anche per valori negativi della
variabile Z:
P ( −z < Z < 0 ) = P ( 0 < Z < z )
inoltre
P ( −∞ < Z < −z ) = P ( z < Z < +∞ ) =
= P ( 0 < Z < +∞ ) − P ( 0 < Z < z ) =
F(z) = P(0 < Z < z)
=
Valori dell’integrale di probabilità della distribuzione normale standardizzata
1
− P (0 < Z < z)
2
128
Come si legge la
Tavola di Sheppard
In questa tavola sono indicati i
valori per cui è:
F(z) = P(−∞ < Z < z)
Esempio
Per calcolare P(1,43<Z<2,56)
occorre fare, con la prima delle
tavole allegate:
P(0<Z<2,56)-P(0<Z<1,43)=
=0,4948-0,4236=0,0712
Con la seconda tavola:
P(Z<2,56)-P(Z<1,43)=
0,9948-0,9236=0,0712
La curva normale
Di questo risultato se ne era già parlato lo scorso anno!
La curva normale e…
Link su collezioni.scuola.zanichelli.it