Esercizi
Uno studente misura il diametro di una popolazione di 100 cellule, trovando come risultato
per il valor medio: dmedio = 8.03 ± 0.06 mm
Supponendo che la distribuzione dei valori sia di tipo gaussiano, trovare l’intervallo [x1, x2],
simmetrico rispetto al valor medio, corrispondente alla probabilità dell’85% che una misura
vi cada all’interno.
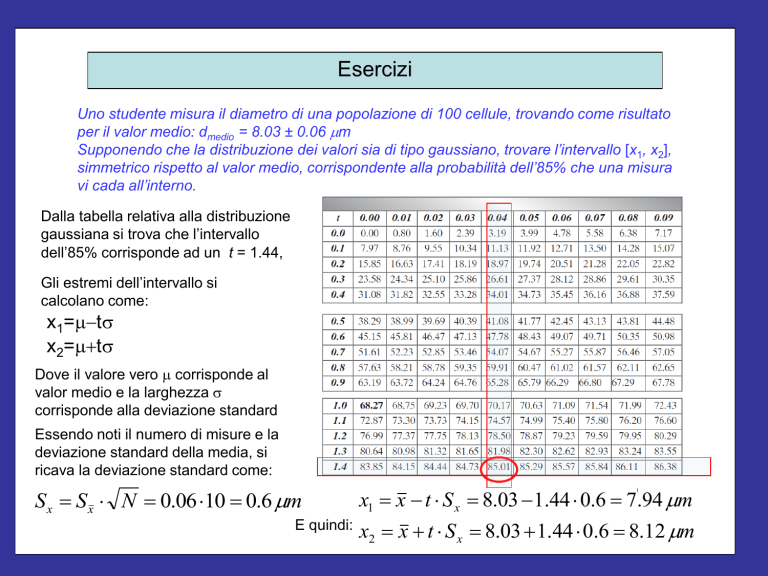
Dalla tabella relativa alla distribuzione
gaussiana si trova che l’intervallo
dell’85% corrisponde ad un t = 1.44,
Gli estremi dell’intervallo si
calcolano come:
x1=m-ts
x2=m+ts
Dove il valore vero m corrisponde al
valor medio e la larghezza s
corrisponde alla deviazione standard
Essendo noti il numero di misure e la
deviazione standard della media, si
ricava la deviazione standard come:
S x S x N 0.06 10 0.6 mm
E quindi:
x1 x - t S x 8.03 - 1.44 0.6 7.94 mm
x2 x + t S x 8.03 + 1.44 0.6 8.12 mm
Esercizi
In un allevamento ci sono 23000 pecore il cui peso medio è di 45.5 ± 0.05 kg.
Se i pesi degli ovini sono distribuiti secondo una curva gaussiana, dare il numero N1 dei capi con
peso compreso tra 43 e 48 kg e il numero N2 dei capi con peso inferiore a 55 kg
La distribuzione del peso degli ovini è centrata sul valore medio 45.5 kg con deviazione standard
pari a:
S x S x N 0.05 23000 7.6 kg
Per il calcolo di N1 si ha a che fare con un intervallo simmetrico [43-48] kg rispetto al valore medio
45.5 kg. Per il calcolo della probabilità associata a tale intervallo si ricava dapprima il valore di t e poi
si guarda la tabella della gaussiana:
x1 x - t S x
x2 x + t S x
45.5 - 43
0.33
7.6
48 - 45.5
48 45.5 + t 7.6 t
0.33
7.6
43 45.5 - t 7.6 t
Vi è quindi una probabilità del 25.86% che le pecore
abbiano un peso tra 43 e 48 kg. Essendo le pecore totali
23000 ne consegue che:
N1 23000
25.86
5948
100
(segue)
Esercizi
In un allevamento ci sono 23000 pecore il cui peso medio è di 45.5 ± 0.05 kg.
Se i pesi degli ovini sono distribuiti secondo una curva gaussiana, dare il numero N1 dei capi con
peso compreso tra 43 e 48 kg e il numero N2 dei capi con peso inferiore a 55 kg
Per il calcolo di N2 si ha a che fare con un intervallo NON simmetrico. Il numero di ovini con peso
inferiore a 55 kg si trova andando a determinare dapprima il valore di t corrispondente a 55:
t
55 - 45.5
1.25
7.6
Dalla tabella della gaussiana, si trova che P(t=1.25) = 78.37% e corrisponde
all’a probabilità di avere ovini con peso compreso tra 36 e 55 kg
0.06
0.06
0.05
0.05
0.04
0.04
0.03
0.03
0.02
0.02
0.01
0.01
0.00
15 20 25 30 35 40 45 50 55 60 65 70 75
0.00
15 20 25 30 35 40 45 50 55 60 65 70 75
Devo tuttavia considerare anche tutti gli ovini con peso inferiore ai 36 kg (coda a sinistra della curva).
(segue)
Esercizi
In un allevamento ci sono 23000 pecore il cui peso medio è di 45.5 ± 0.05 kg.
Se i pesi degli ovini sono distribuiti secondo una curva gaussiana, dare il numero N1 dei capi con
peso compreso tra 43 e 48 kg e il numero N2 dei capi con peso inferiore a 55 kg
E’ sufficiente ricordarsi che l’area totale sottesa dalla gaussiana corrisponde al 100%
0.06
0.05
100 - 78.37
%
2
0.04
0.03
78.37%
La probabilità di avere un peso inferiore a
55 kg è quindi pari a :
P peso 55kg 50 +
78.37
89.185%
2
Da cui il numero di pecore: :
0.02
N1 23000
0.01
0.00
15 20 25 30 35 40 45 50 55 60 65 70 75
89.185
20513
100
Esercizi
Una grandezza è distribuita normalmente attorno al valore 30 con deviazione standard pari a 3.
Quale è la percentuale di misure che ci aspetta essere comprese tra 31 e 33?
L’intervallo considerato è un intervallo non simmetrico in cui entrambi gli estremi si trovano a destra
del valore centrale della distribuzione:
x1=m-t1s
x2=m+t2s
Sostituendo i valori degli estremi x1 e x2, del valore medio e della deviazione
standard si ricavano i due valori di t :
31 - 30
0.33
3
33 - 30
t2
1
3
t1
Dalla tabella della gaussiana si trova:
P(t1)= 25.86 % (figura A) e P(t2)=68.27 % (figura B)
(segue)
Esercizi
Una grandezza è distribuita normalmente attorno al valore 30 con deviazione standard pari a 3.
Quale è la percentuale di misure che ci aspetta essere comprese tra 31 e 33?
Guardando le curve la probabilità associata all’intervallo non simmetrico si ricava come:
P31 x 33
P(t 2 ) P(t1 )
21.2%
2
2
Esercizi
Sia data una distribuzione centrata intorno a 25 con larghezza sigma 1.3. Trovare:
(a) l’intervallo corrispondente alla probabilità del 68.27%;
(b) La probabilità di trovare un valore compreso tra 21.9 e 25.5.
a) La probabilità del 68.27% corrisponde all’intervallo: [m-s; m+s]
Quindi:
0.35
0.30
m - s 25 - 1.3 23.7
m + s 25 + 1.3 26.3
0.25
0.20
0.15
b) L’intervallo è non simmetrico.
Calcolo i valori di t relativi ai due estremi:
25 - 21.9
2.38
1.3
25.5 - 25
t2
0.385
1 .3
0.10
0.05
t1
Dalla tabella della gaussiana:
P(t1)= 98.27 %
P(t2)= 30 %
(segue)
0.00
20
21
22
23
24
25
26
27
28
29
26
27
28
29
30
0.35
0.35
0.30
0.30
P(t1)
0.25
0.25
0.20
0.20
0.15
0.15
0.10
0.10
0.05
0.05
0.00
20
21
22
23
24
25
26
27
28
29
30
P(t2)
0.00
20
21
22
23
24
25
30
Esercizi
Sia data una distribuzione centrata intorno a 25 con larghezza sigma 1.3. Trovare:
(a) l’intervallo corrispondente alla probabilità del 68.27%;
(b) La probabilità di trovare un valore compreso tra 21.9 e 25.5.
0.35
0.35
0.30
0.30
P(t1) /2
0.25
P(t2) /2
0.25
0.20
0.20
0.15
0.15
0.10
0.10
0.05
0.05
0.00
20
21
22
23
24
25
26
27
28
29
30
0.00
20
21
22
Osservando le aree e sfruttando la simmetria della curva si trova:
P21.9 x 25.5
P(t1 ) P(t 2 )
+
64%
2
2
23
24
25
26
27
28
29
30