Lezione 8
Funzioni e formule trigonometriche
Donato A. Ciampa
In questa lezione introdurremo i concetti fondamentali della trigonometria: definiremo le funzioni trigonometriche seno, coseno,
tangente, cotangente, secante, cosecante; analizzeremo le relazioni
che le legano tra loro; infine, tratteremo le formule trigonometriche
e le loro principali applicazioni.
1. Le funzioni trigonometriche
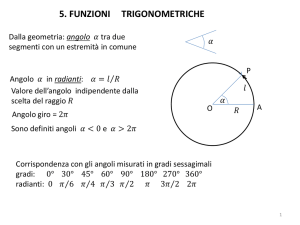
1.1. Misure di angoli ed archi. Misurare un angolo significa compararlo con un
altro angolo, scelto come unità. Ad ogni arco di circonferenza corrisponde un unico
angolo al centro. La misura di un arco è, quindi, la misura dell’angolo al centro
che vi corrisponde. In trigonometria si adoperano tre diverse unità di misura per
gli angoli:
• il grado sessagesimale, definito come la novantesima parte dell’angolo retto;
• il grado centesimale, definito come la centesima parte dell’angolo retto;
• il radiante.
Vediamo nel dettaglio come si definisce quest ultimo.
Sia C una circonferenza di centro O e raggio r e sia AB un arco determinato dai
punti A e B su di essa. Sia ` > 0 la lunghezza dell’arco AB: per definizione, la
\ che sottende l’arco AB è il rapporto
misura in radianti dell’angolo al centro AOB
`/r.
Si osservi che se `/r = 1, allora ` = r: in altre parole, l’unità di misura in
questo sistema, detta radiante, è l’angolo al centro che sottende un arco pari alla
lunghezza del raggio della circonferenza. Se ne deduce che la misura dell’angolo di
360 gradi, sottendendo tale angolo l’intera circonferenza, corrisponde a 2π radianti.
In generale, la misura in radianti αrad di un angolo α è correlata a quella in gradi
sessagesimali αgrad dalla relazione
αrad =
2π
αgrad .
360
La trigonometria è la branca della matematica che studia le relazioni intercorrenti tra i lati e gli angoli dei triangoli. Per poter definire delle formule che permettano di calcolare, ad esempio, la lunghezza dei lati di un triangolo scaleno una
volta noti i suoi angoli, è necessario introdurre delle particolari funzioni, dette funzioni trigonometriche, definite per ogni angolo α espresso in radianti e a valori (in
generale) nell’insieme dei numeri reali.
Per fare questo, sia C := {(x, y) ∈ R : x2 + y 2 = 1} la circonferenza unitaria di
centro il punto O(0, 0) e raggio r = 1, rappresentata in figura:
1
2
6
y
#
# Q(1, γ)
P (α, β)##
#
#
#
#
#
#
O
#
θ
H
K
x
L’ascissa a del punto P viene detta coseno dell’angolo θ, l’ordinata b viene detta
seno dell’angolo c, mentre l’ordinata γ del punto Q viene detta tangente dell’angolo
θ: in simboli
a = cos θ,
b = sin θ,
c = tan θ.
2
2
Poiché P ∈ C, si ha a + b = 1, e quindi
cos2 θ + sin2 θ = 1,
(1.1)
che è detta relazione fondamentale della trigonometria.
Se consideriamo i triangoli OP H e OQH, essi risultano simili in quanto hanno
gli stessi angoli interni. Ne segue che
KQ : P H = OK : OH.
Ma
KQ = c = tan θ,
P H = b = sin θ,
OK = 1,
OH = a = cos θ,
e quindi
tan θ
1
=
,
sin θ
cos θ
da cui la relazione
sin θ
.
cos θ
Si definiscono poi le funzioni cosecante, secante, cotangente di θ al modo seguente
1
1
1
cos θ
csc θ =
,
sec θ =
,
cot θ =
=
.
sin θ
cos θ
tan θ
sin θ
(1.2)
tan θ =
3
Le funzioni trigonometriche godono di alcune proprietà fondamentali che possiamo riassumere nella seguente tabella:
sin x
cos x
R
R
Dominio
Periodicità T = 2π
tan x
R\
nπ
o
+ kπ, k ∈ Z
2
T = 2π
T =π
Dominio
ristretto
[−π, π]
[−π, π]
³ π π´
− ,
2 2
Simmetrie
Dispari
Pari
Dispari
È inoltre immediato verificare che
sin 0 = 0,
sin
cos 0 = 1,
sin
sin
1
π
= ,
6
2
cos
π
1
= ,
6
2
π
= 1,
2
sin
π
= 0,
2
sin
sin π = 0,
√
π
2
=
,
4
2
sin
cos π = −1,
√
π
2
=
,
4
2
sin
sin
3π
= −1,
2
√
π
3
=
,
3
2
cos
3π
= 0,
2
√
π
3
=
,
3
2
2. Relazioni tra archi associati ed espressione in termini di una sola
funzione trigonometrica
Si dicono archi associati due angoli la cui somma o differenza è un angolo notevole. In particolare, se x, y sono i due archi, essi si dicono:
(1) complementari se x + y = π/2;
(2) supplementari se x + y = π;
(3) esplementari se x + y = 2π.
Valgono le seguenti relazioni per gli archi associati:
4
sin
³π
cos
³π
´
− x = sin x
tan
³π
2
³π
´
cos
+ x = − sin x
2
sin (π − x) = sin x
cos (π − x) = − cos x
tan (π − x) = − tan x
sin (π + x) = − sin x
cos (π + x) = − cos x
tan (π + x) = tan x
2
µ
¶
3π
− x = − cos x
2
µ
¶
3π
sin
+ x = − cos x
2
sin
sin (2π − x) = − sin x
sin (−x) = − sin x
tan
2
³π
´
− x = cot x
´
+ x = cos x
sin
2
³π
´
− x = cos x
2
´
+ x = − cot x
µ
¶
µ
¶
3π
3π
− x = − sin x tan
− x = cot x
2
2
µ
¶
µ
¶
3π
3π
cos
+ x = sin x tan
+ x = − cot x
2
2
cos
cos (2π − x) = cos x
cos (−x) = cos x
tan (2π − x) = − tan x
tan (−x) = − tan x.
È possibile poi, utilizzando le (1.1) e (1.2), esprimere le funzioni trigonometriche
sin x, cos x e tan x in funzione di una sola delle altre. in particolare si ha1:
Espressione in funzione di sin x.
p
(2.1)
cos x = ± 1 − sin2 x,
sin x
tan x = ± p
1 − sin2 x
;
Espressione in funzione di cos x.
(2.2)
sin x = ±
√
p
1 − cos2 x,
tan x = ±
1 − cos2 x
;
cos x
Espressione in funzione di tan x.
(2.3)
sin x = ± √
tan x
2
1 + tan x
tan x = ± √
,
1
1 + tan2 x
.
1Il segno ± va scelto a seconda che l’angolo x si trovi nel primo, secondo, terzo o quarto
quadrante, in accordo con la seguente tabella che riassume le relazione tra il segno della funzione
trigonometrica e il quadrante in cui si trova l’angolo x:
sin x
cos x
tan x
I
+
+
+
II
+
−
−
III
−
−
+
IV
−
+
−
5
3. Formule trigonometriche
Come abbiamo visto prima, è facile stabilire il valore di una delle funzioni trigonometriche quando si lavora su archi associati. Tuttavia, risulta spesso utile conoscere
il valore di una delle funzioni trigonometriche anche su angoli che si possano esprimere come somma, differenza (o altro ancora) di due o più archi (non necessariamente associati). Di seguito riportiamo tali formule.
Formule di sottrazione.
(3.1)
sin(x − y) = sin x cos y − sin y cos x;
(3.2)
cos(x − y) = cos x cos y + sin x sin y;
tan x − tan y
tan(x − y) =
.
1 + tan x tan y
(3.3)
Formule di addizione.
(3.4)
sin(x + y) = sin x cos y + sin y cos x;
(3.5)
cos(x + y) = cos x cos y − sin x sin y;
tan x + tan y
tan(x + y) =
.
1 − tan x tan y
(3.6)
Formule di duplicazione.
(3.7)
sin 2x =2 sin x cos x;
(3.8)
cos 2x = cos2 x − sin2 x = 2 cos2 x − 1 = 1 − 2 sin2 x;
2 tan x
tan 2x =
.
1 − tan2 x
(3.9)
Formule di bisezione.
(3.10)
(3.11)
(3.12)
r
x
1 − cos x
sin = ±
;
2
2
r
1 + cos x
x
cos = ±
;
2
2
r
x
1 − cos x
tan = ±
.
2
1 + cos x
Espressione in funzione di t = tan(x/2).
(3.13)
(3.14)
(3.15)
2t
;
1 + t2
1 − t2
;
cos x =
1 + t2
2t
tan x =
.
1 − t2
sin x =
6
Formule di prostaferesi.
x+y
x−y
cos
;
2
2
x−y
x+y
cos
;
=2 sin
2
2
x+y
x−y
=2 cos
cos
;
2
2
x+y
x−y
= − 2 sin
sin
;
2
2
sin(x ± y)
.
=
cos x cos y
(3.16)
sin x + sin y =2 sin
(3.17)
sin x − sin y
(3.18)
cos x + cos y
(3.19)
cos x − cos y
(3.20)
tan x ± tan y
Formule di Werner.
1
sin x sin y = [cos(x − y) − cos(x + y)] ;
2
1
sin x cos y = [sin(x + y) + sin(x − y)] ;
2
1
cos x cos y = [cos(x + y) + cos(x − y)] .
2
(3.21)
(3.22)
(3.23)
4. Funzioni trigonometriche inverse
Se consideriamo la funzione sin x ristretta al solo dominio [−π/2, π/2], ci accorgiamo che su tali valori la funzione seno assume tutti i valori compresi tra −1 e 1
una ed una sola volta. Ne segue che la funzione
h π πi
sin : − ,
−→ [−1, 1],
2 2
risulta biettiva e quindi invertibile. La funzione
h π πi
arcsin : [−1, 1] −→ − ,
,
2 2
è detta arco seno di x, è la funzione inversa della funzione seno ed è definita da
y = arcsin x ⇐⇒ x = sin y.
Allo stesso modo, si possono definire le funzioni inverse di coseno e tangente.
Abbiamo la funzione
arccos : [−1, 1] −→ [0, π] ,
detta arco coseno di x, definita da
y = arccos x ⇐⇒ x = cos y.
Infine la funzione
h π πi
,
arctan : R −→ − ,
2 2
detta arco tangente di x, definita da
y = arctan x ⇐⇒ x = tan y.
Non tratteremo ulteriormente tali funzioni, in quanto esse verranno ampiamente
studiate al corso di analisi in una variabile reale.