Esercizi di econometria: serie 4
Esercizio 1
Siano X, Y e Z variabili casuali distribuite secondo la legge multinomiale di parametri n, p1 ,
p2 , p3 =1 - p1 - p2. . Calcolare la Covarianza tra le variabili X ed Y.
Soluzione
Date due variabili X e Y definite sullo stesso spazio di probabilità, la loro covarianza,
indicata con Cov(X,Y) è definita come:
Cov(X,Y)=E(X,Y)- E(X)E(Y).
Date tre variabili casuali X, Y e Z distribuite secondo una legge multinomiale di parametri n,
p1 , p2 , p3 =1-p1-p2 , si osserva che le distribuzioni marginali ad essa relativa sono delle
distribuzioni binomiali.
Di conseguenza la funzione marginale di X è f X(x)∼B(n, p1 ) il cui valore atteso è E(X)=np 1 ,
mentre la funzione marginale di Y è f Y(y)∼B(n, p2 ) il cui valore atteso è E(Y)=np 2 .
Rimane ora da calcolare il valore atteso del prodotto delle variabili casuali X e Y che è pari a:
E (XY ) = ∑∑ f XY (x, y)xy = ∑∑
x
y
x
y
n!
p x1 ⋅ p y2 (1 − p1 − p 2 )n − x − y xy
x!y!(n − x − y )!
Sulla base della formula definita per la covarianza, si ha:
n!
n− x − y
Cov(X,Y) = ∑∑
p x1 ⋅ p y2 (1 − p1 − p 2 )
xy − (np 1 )(np 2 )
x y x!y!(n − x − y)!
Esercizio 2
Un giocatore di roulette scommette 2 lire sul rosso ed 1 lira sulla serie {1, 2,......,12}. Sia
X={Vincita dalla scommessa sul rosso} e Y = {vincita dalla scommessa sulla dodicina}.
a. Si determini la varianza di X e di Y.
b. Si determini la covarianza tra X ed Y.
Soluzione
Siano così definiti due eventi:
X=vincita dalla scommessa sul rosso ⇒ sul rosso scommetto 2 lire
Y=vincita dalla scommessa sulla dodicina ⇒ sulla dodicina 1 lire
Tanto l’uscita del rosso (Vx ) che della dodicina (VY) sono eventi bernoulliani così definiti:
18
1
con
p
=
1
38
VX =
0 con 1 - p1 = 20
38
12
1
con
p
=
2
38
VY =
0 con 1 - p 2 = 26
38
Vincita = scommessa ⋅[valore della vincita⋅(V-1)], da cui:
30
Esercizi di econometria
X=2(2VX-1)
serie 4
Y=1(3VY-1)
entrambe trasformazioni lineari di variabili casuali bernoulliane.
a. Ricordando che il valore atteso e la varianza di una variabile casuale bernoulliana sono
rispettivamente E(X) = p e Var(X) = pq = p(1-p), abbiamo:
Var(VX)=p1 (1- p1 )=(18·20)/382
Var(VY)=p2 (1- p2 )=(12·26)/382 .
Sulla base della proprietà della varianza Var(aX+b) = a2 Var(X), si deduce:
Var(X)=Var[2(2VX-1)]=16Var(X)
Var(Y)=Var[1(3VY-1)]=9Var(Y)
b. Per la covarianza il risultato è 36/361.
Esercizio 3
Siano X ed Y distribuite in forma bivariata normale ed indipendente con medie nulle e
varianze unitarie
a. Ricavare la funzione di densità congiunta
b. Calcolare P(X≤0 Y ≤0)
c. Calcolare la distribuzione di X+Y
Soluzione
a. Date due variabili casuali X e Y distribuite in forma bivariata normale ed indipendente con
medie nulle e varianze unitarie, la funzione di densità congiunta è così definita:
1
1
f XY ( x , y ) =
exp− (x 2 + y 2 )
2π
2
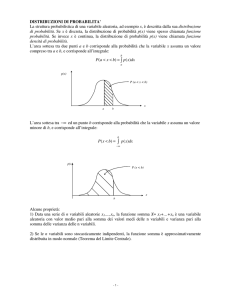
b. Graficamente la soluzione al quesito è ovvia, basta
osservare la figura riportata qui a fianco. Su di un piano
cartesiano è stata riportata la funzione normale
standardizzata bivariata, la cui area totale è pari ad 1.
Poiché si richiede di calcolare l’area della curva
contenuta nel terzo quadrante, per le caratteristiche di
simmetria della stessa possiamo dire che il valore è pari a
0,25.
Analiticamente invece il problema si risolve integrando la curva tra (-∞,0), ossia svolgendo il
seguente integrale:
P (X ≤ 0; Y ≤ 0 ) =
0
0
0
1 - 12 (x 2 + y 2 )
1 - 12 x 2
1 - 1 y2
1 1 1
e
dy = ∫
e
dx ⋅ ∫ e 2 dy = ⋅ =
2 2 4
−∞ 2π
− ∞ 2π
−∞ 2π
0
∫ dx ∫
−∞
31
Esercizi di econometria
serie 4
1 - 12 x 2
1 - 12 y 2
e
e f Y (y ) =
e
sono funzioni di normali standardizzate,
2π
2π
il cui integrale tra (-∞,0) è pari a 0.5, dato che tra (-∞,∞) è pari all’unità e la curva è
simmetrica rispetto allo zero.
questo perché f X (x ) =
c. Date X e Y che si distribuiscono normalmente rispettivamente con medie µx = µy = 0 e
scarti quadratici medi σx = σy = 1, la variabile W, definita come somma delle variabili appena
citate, si distribuisce anch’essa come una normale con media pari alla somma delle medie e
varianza pari alla somma delle varianze. Quindi: W=(X+Y)∼N(0,2) e la funzione di densità è
la seguente: f W (w ) =
w2
1 w − 0 2
1
exp−
= 0.282e 4 .
2π ⋅ 2
2 2
Esercizio 4
Sono date le due variabili casuali X ed Y con funzione di densità congiunta:
1
−( x + y )
f XY ( x , y ) = 3 ( x + 2 y )e
0
x, y ≥ 0
altrimenti
a. Trovare le due funzioni di densità marginali
b. Trovare la funzione di densità di X condizionata ad Y
c. Provare che P(Y>X) = 7/12
Soluzione
a. la funzione di densità marginale di X è la seguente:
f X (x ) =
∞
∫
0
∞
1
1 - x ∞ -y
2 -x ∞ -y
-( x + y )
f XY (x , y ) dy = ∫ (x + 2 y )e
dy = xe ∫ e dy + e ∫ ye dy
3
3
3
0
0
0
dove:
∞
∞
0
0
-y
-y ∞
-y
-y ∞
-y ∞
∫ e dy = [ − e ]0 = 1 e ∫ ye dy = [ − ye ]0 − [e ]0 = 1 (per l’integrazione per parti).
In definitiva la funzione marginale di X è:
f X (x ) =
1 -x 2 -x 1 -x
xe + e = e ( x + 2 )
3
3
3
La funzione marginale di Y invece è:
∞
∞
∞
∞
1
( x + 2y )e -(x + y ) dx = 1 e - y ∫ xe - x dx + 2 ye - y ∫ e -x dx = 1 e - y ( 1 + 2 y )
3
3 0
3
3
0
0
f Y (y ) = ∫ f XY ( x , y ) dx = ∫
0
32
Esercizi di econometria
serie 4
b. Per quanto riguarda la funzione di densità di X condizionata ad Y, i casi che si possono
verificare sono due:
Ø se X ed Y sono due variabili casuali indipendenti, tale funzione è pari a quella di densità
incondizionata della X;
Ø se invece X ed Y non sono due variabili casuali indipendenti allora:
1
( x + 2y )e -(x + y ) (x + 2 y )e - x
f XY (x , y ) 3
f X |Y ( x | y ) =
=
=
1 -y
f Y (y)
( 1 + 2y )
e ( 1 + 2y )
3
c. Bisogna ora dimostrare che la P(Y>X) = 7 12
Per il calcolo della probabilità che X sia maggiore di Y utilizziamo la seguente formulazione:
∞
∞
∫ dx∫ 3(x + 2y ) e
0
1
−x − y
dy
x
ponendo la condizione che Y sia maggiore di X, in quanto l’integrale è per un valore di Y che
varia tra x ad ∞
∞ ∞
1 −x −y 2 −x−y
1
− x− y
∫0 dx∫x 3(x + 2y)e dy = ∫0 ∫x 3 xe + 3 ye dy dx
∞
∞
Risolviamo l’integrale tra parentesi quadre spezzandolo in 2 integrali distinti
∞
1 −x −y
1 −x ∞ −y
1
1) ∫ xe
dy = xe ∫ e dy = xe - x − e −y
3
3
x 3
x
[
{[
∞
2)
]
1
= xe −2 x
3
∞
x
2 −x−y
2 −x ∞ −y
2
ye
dy
=
e ∫ ye dy = e -x − ye−y
∫x 3
3
3
x
] − [e ]
∞
x
−y ∞
x
}= 23 e
−x
(xe
−x
+ e−x )
Sostituendo abbiamo:
∞
∞
∞
∞
1 − 2x
2 −2 x
7
2 −x
−2 x 2 − 2 x
−x
−x
-2x
∫0 3 e xe + e + 3 xe dx = ∫0 xe + 3 e dx = ∫0 xe dx + ∫0 3 e dx = 12 cvd
(
)
Infatti è facile verificare, utilizzando l’integrazione per parti, che:
∞
- 2x
∫ xe dx =
0
1
4
∞
e
2
∫3 e
0
−2 x
dx =
1
3
Esercizio 5
Siano X ed Y variabili casuali normali bivariate con medie rispettivamente 1 e 2 e varianze
rispettivamente 2 e 4. Sia inoltre Corr(X, Y) = 0.5.
a. Si derivi la funzione di densità marginale della Y
33
Esercizi di econometria
serie 4
b. Si derivi la funzione di densità della X condizionata ad Y=0
c. Esistono condizioni sotto le quali X ed Y sono indipendenti?
Soluzione
a. Al fine di derivare la funzione di densità marginale della Y, si ricordi che se due variabili
X e Y sono distribuite congiuntamente come una normale multivariata, le distribuzioni
marginali di X e Y sono distribuzioni normali unidimensionali; cioè X è distribuito
normalmente con media µX e varianza ó 2X , e Y è distribuito normalmente con media µY e
varianza ó Y2 ; per cui sostituendo i relativi valori si ha:
(y - 2 )2
1 y − µ 2
1
y
= 0.2 e 8 .
f Y (y ) =
exp−
2
σ
2πσ2y
y
b. Per poter derivare la funzione di densità della X condizionata ad Y=0 nel modo più
agevole, si ricordi che se due variabili X e Y sono distribuite congiuntamente come una
normale multivariata, la distribuzione condizionata di X dato Y = y è normale con media
ó
µ X + ñ X (y − µ y ) e varianza σ 2X 1 − ρ 2
óY
per cui sostituendo nell’espressione i valori dati si ha che tale funzione si distribuisce
(
f X |Y ( x | y = 0 ) =
)
f XY ( x , y )
∼N(0,29;3/2) quindi
f Y (y = 0 )
f (x , y)
f X |Y ( x | y = 0 ) = XY
= 0.325 e
f Y ( y = 0)
(x - 0.29)2
3
.
c. In generale il concetto di covarianza definisce un caso particolare di dipendenza, ossia
quella di tipo lineare. Ciò significa che Cov(X,Y)=0, e di conseguenza Corr(X,Y)=0, non
implica necessariamente che X ed Y siano indipendenti, mentre sussiste la relazione inversa
per cui se X ed Y sono indipendenti allora Cov(X,Y)=0 e quindi anche la correlazione.
Tutto ciò vale in generale, ma nel caso di una normale bivariata la relazione vale in entrambi i
sensi, ossia:
INDIPENDENZA ⇔ CORRELAZIONE UGUALE A ZERO.
Di conseguenza essendo la Corr(X,Y)=0.5 non sussistono condizioni per cui le variabili
siano indipendenti.
Esercizio 6
E’ dato un campione casuale di dimensione n=2 estratto da una popolazione uniforme
nell’intervallo reale (0,1).
a. Qual è la probabilità che due osservazioni di tale campione non differiscano più di 0.5?
b. Qual è la probabilità che la loro semisomma sia maggiore di 0.6?
Soluzione
Data una distribuzione uniforme così definita:
34
Esercizi di econometria
1
f XY ( x , y ) =
0
serie 4
0 < x < 1e 0 < y < 1
altrimenti
a. Si chiede di calcolare P(|X-Y|≤0.5). Risolviamo il quesito mediante un approccio grafico:
Come si può notare trovare la probabilità sopra indicata significa calcolare l’area tratteggiata,
che si ottiene sottraendo all’area del quadrato l’area dei due triangoli uguali e di cui sono note
le dimensioni, ossia:
P(|X-Y|≤0.5)=1-2[(0.5⋅0.5)/2]=3/4=0.75 ⇒ 75%.
( X + Y)
b. Ora si tratta di trovare P
> 0.6 che calcoleremo sempre osservando la
2
rappresentazione grafica.
Come si può notare calcolare la probabilità sopra indicata significa trovare l’area del
triangolo tratteggiato, quindi:
P
(X + Y ) > 0.6 = (0.8) ⋅ (0.8 ) = 0.32
2
2
⇒ 32%.
35