DISTRIBUZIONI DI PROBABILITA'
La struttura probabilistica di una variabile aleatoria, ad esempio x, è descritta dalla sua distribuzione
di probabilità. Se x è discreta, la distribuzione di probabilità p(x) viene spesso chiamata funzione
probabilità. Se invece x è continua, la distribuzione di probabilità p(x) viene chiamata funzione
densità di probabilità.
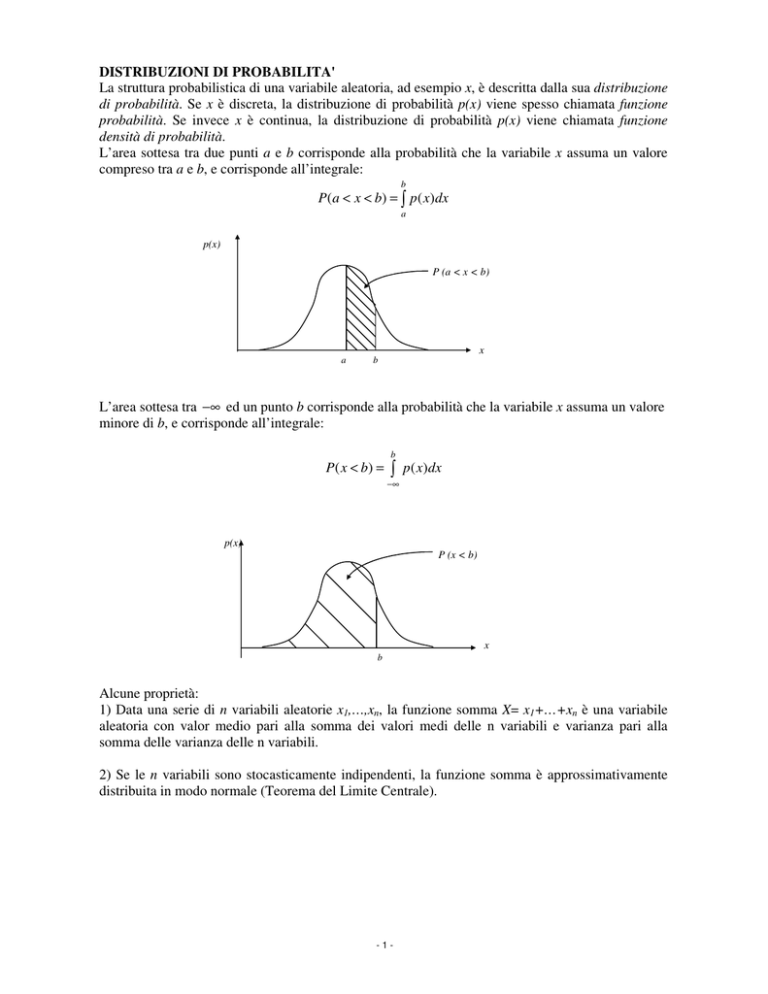
L’area sottesa tra due punti a e b corrisponde alla probabilità che la variabile x assuma un valore
compreso tra a e b, e corrisponde all’integrale:
b
P(a < x < b) = ∫ p ( x)dx
a
p(x)
P (a < x < b)
x
a
b
L’area sottesa tra −∞ ed un punto b corrisponde alla probabilità che la variabile x assuma un valore
minore di b, e corrisponde all’integrale:
b
P( x < b) =
∫ p( x)dx
−∞
p(x)
P (x < b)
x
b
Alcune proprietà:
1) Data una serie di n variabili aleatorie x1,…,xn, la funzione somma X= x1+…+xn è una variabile
aleatoria con valor medio pari alla somma dei valori medi delle n variabili e varianza pari alla
somma delle varianza delle n variabili.
2) Se le n variabili sono stocasticamente indipendenti, la funzione somma è approssimativamente
distribuita in modo normale (Teorema del Limite Centrale).
-1-
DISTRIBUZIONE DI PROBABILITA' NORMALE
Un particolare tipo di distribuzione per una variabile continua x è la DISTRIBUZIONE
NORMALE. La funzione densità di probabilità di una variabile aleatoria x distribuita normalmente
è uguale a:
1 x− µ
σ
2
−
1
p ( x) =
e 2
σ 2π
dove −∞ < µ < +∞ è il valore medio della distribuzione e σ 2 > 0 è la varianza. Tale funzione si
indica con N( µ ,σ). Le probabilità che la variabile x distribuita normalmente si trovi all'interno di
un intervallo centrato attorno al valor medio µ di semi-ampiezza rispettivamente pari a σ, 2σ, 3σ
sono:
P{ µ −σ ≤ x ≤ µ + σ
} ≅ 68%
P { µ − 2 ⋅σ ≤ x ≤ µ + 2 ⋅σ
} ≅ 95%
P { µ − 3 ⋅σ ≤ x ≤ µ + 3 ⋅σ
} ≅ 99%
La probabilità che la variabile x sia minore di un valore b sarà invece pari a:
1 x−µ
σ
b
2
−
1
P( x < b) = ∫
e 2
−∞ σ 2π
dx
Il calcolo di questo integrale può essere agevolmente effettuato utilizzando il cambiamento di
variabile:
z=
x−µ
σ
per cui si ottiene:
1
z*
b − µ z* 1 − 2 z
P ( x < b ) = P z < z* =
e
dz = ∫ f u ( z )dz
= ∫
σ −∞ 2π
−∞
2
(1)
La funzione:
1
1 − 2z
fu ( z ) =
e
2π
2
è la funzione la funzione densità di probabilità normalizzata, si indica con N(0,1), ed è una
funzione densità di probabilità normale con valor medio nullo e varianza unitaria.
L’integrale (1) della funzione densità di probabilità normalizzata si trova tabulato nella pagina
seguente.
-2-
-3-












