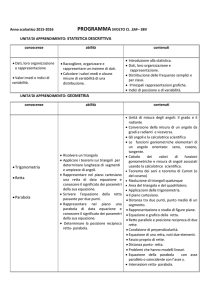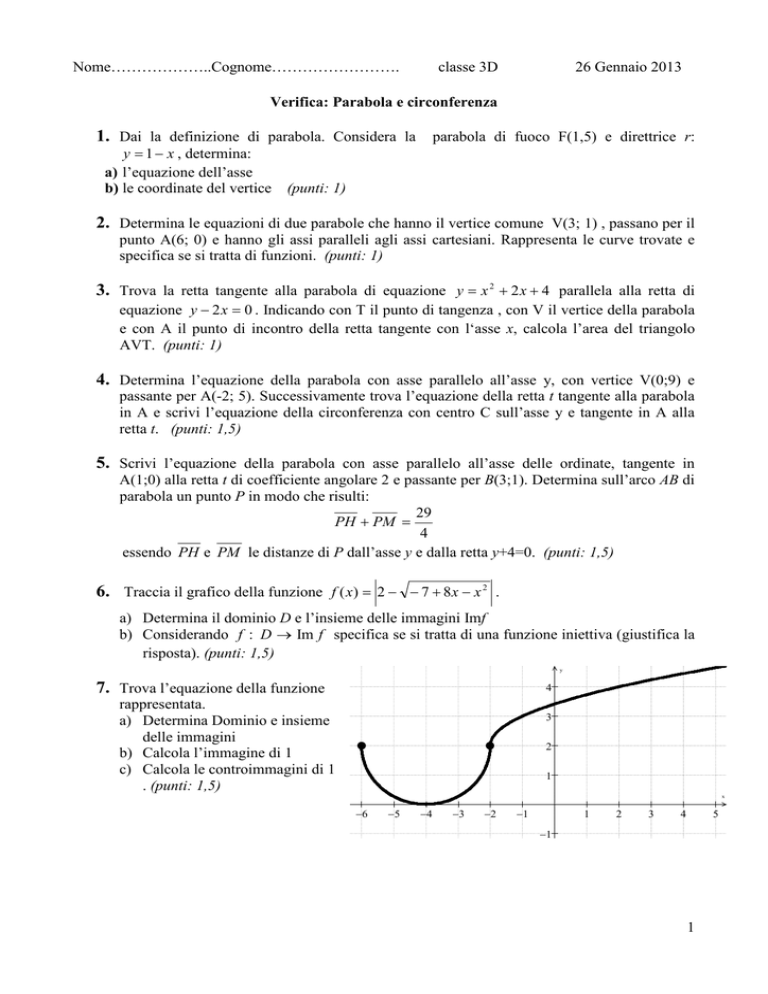
Nome………………..Cognome…………………….
classe 3D
26 Gennaio 2013
Verifica: Parabola e circonferenza
1. Dai la definizione di parabola. Considera la parabola di fuoco F(1,5) e direttrice r:
y = 1 − x , determina:
a) l’equazione dell’asse
b) le coordinate del vertice
(punti: 1)
2. Determina le equazioni di due parabole che hanno il vertice comune V(3; 1) , passano per il
punto A(6; 0) e hanno gli assi paralleli agli assi cartesiani. Rappresenta le curve trovate e
specifica se si tratta di funzioni. (punti: 1)
3. Trova la retta tangente alla parabola di equazione y = x 2 + 2 x + 4 parallela alla retta di
equazione y − 2 x = 0 . Indicando con T il punto di tangenza , con V il vertice della parabola
e con A il punto di incontro della retta tangente con l‘asse x, calcola l’area del triangolo
AVT. (punti: 1)
4. Determina l’equazione della parabola con asse parallelo all’asse y, con vertice V(0;9) e
passante per A(-2; 5). Successivamente trova l’equazione della retta t tangente alla parabola
in A e scrivi l’equazione della circonferenza con centro C sull’asse y e tangente in A alla
retta t. (punti: 1,5)
5. Scrivi l’equazione della parabola con asse parallelo all’asse delle ordinate, tangente in
A(1;0) alla retta t di coefficiente angolare 2 e passante per B(3;1). Determina sull’arco AB di
parabola un punto P in modo che risulti:
29
PH + PM =
4
essendo PH e PM le distanze di P dall’asse y e dalla retta y+4=0. (punti: 1,5)
6. Traccia il grafico della funzione f ( x) = 2 − − 7 + 8 x − x 2 .
a) Determina il dominio D e l’insieme delle immagini Imf
b) Considerando f : D → Im f specifica se si tratta di una funzione iniettiva (giustifica la
risposta). (punti: 1,5)
y
4
7. Trova l’equazione della funzione
rappresentata.
a) Determina Dominio e insieme
delle immagini
b) Calcola l’immagine di 1
c) Calcola le controimmagini di 1
. (punti: 1,5)
3
2
1
x
−6
−5
−4
−3
−2
−1
1
2
3
4
5
−1
1
Soluzioni verifica 3D 26 Gennaio 2013
1) Dai la definizione di parabola. Considera la parabola di fuoco F(1,5) e direttrice r: y = 1 − x ,
determina:
a) l’equazione dell’asse
b) le coordinate del vertice (punti: 1)
y
9
8
La parabola è il luogo dei punti P del piano
equidistanti da una retta detta direttrice e un punto
detto fuoco
7
6
F
5
L’asse di simmetria è la retta passante per il fuoco,
m =1
perpendicolare
alla
direttrice:
⇒ y − 5 = 1 ⋅ ( x − 1)
y = x+4
Il vertice è il punto medio del segmento FH, dove
H è il punto di intersezione tra asse e direttrice:
3
x=−
y = 1− x
2
⇒
H:
y = x + 4
y = 5
2
3
1−
2 = −1
xV =
2
4
V:
5
5+
2 15
yV = 2 = 4
V
H
4
3
2
1
x
−5
−4
−3
−2
−1
1
2
3
4
5
2) Determina le equazioni di due parabole che hanno il vertice comune V(3; 1) , passano per il punto
A(6; 0) e hanno gli assi paralleli agli assi cartesiani. Rappresenta le curve trovate e specifica se si
tratta di funzioni.
y
4
3
2
V
1
A
−1
1
−1
−2
−3
−4
−5
2
3
4
5
6
x
7
8
9
La parabola con asse verticale appartiene al fascio
di equazione: y − 1 = a ( x − 3) 2 , per determinare a,
è sufficiente imporre il passaggio per A
1
0 − 1 = a (6 − 3) 2 a = −
9
1
1
2
y − 1 = − ( x − 3) 2 ⇒ y = − x 2 + x
9
9
3
E’ una funzione, poiché ad ogni x reale corrisponde
una e una solo y.
La parabola con asse orizzontale appartiene al
fascio di equazione: x − 3 = a ( y − 1) 2 , per
determinare a, è sufficiente imporre il passaggio per
A
6 − 3 = a (0 − 1) 2 a = 3
2
x − 3 = 3( y − 1) 2 ⇒ x = 3 y 2 − 6 y + 6
Non è una funzione, poiché ad ogni x reale o all’interno di un dominio NON corrisponde una e una
solo y.
3) Trova la retta tangente alla parabola di equazione y = x 2 + 2 x + 4 parallela alla retta di
equazione y − 2 x = 0 . Indicando con T il punto di tangenza , con V il vertice della parabola e con
A il punto di incontro della retta tangente con l‘asse x, calcola l’area del triangolo AVT.
La tangente t richiesta ha m = 2 ¸il punto di
tangenza si può determinare imponendo y ' = 2
⇒ T (0;4) , di
2x + 2 = 2 ⇒ x = 0
conseguenza t : y = 2 x + 4
Il vertice della parabole è V (−1; 3) .
Per determinare l’area del triangolo:
y
7
t
6
5
T
4
AT = ( x A − xT ) + ( y A − yT ) = 20 = 2 5
L’altezza è la distanza tra la retta t e il vertice V
2 ⋅ (−1) − 3 + 4
1
h=
=
5
5
AT ⋅ h
Area ( ATV ) =
=1
2
V
2
3
2
1
A
x
−4
−3
−2
−1
1
2
3
4
2
4) Determina l’equazione della parabola con asse parallelo all’asse y, con vertice V(0;9) e passante
per A(-2; 5). Successivamente trova l’equazione della retta t tangente alla parabola in A e scrivi
l’equazione della circonferenza con centro C sull’asse y e tangente in A alla retta t.
y
La parabola appartiene al fascio di equazione:
y − 9 = ax 2 , per determinare a, è sufficiente
imporre il passaggio per A
5 − 9 = 4 a ⇒ a = −1
10
9
V
8
t
7
6
A
5
4
C
3
2
1
x
−6
−5
−4
−3
−2
−1
1
2
3
4
5
6
y = −x 2 + 9
La retta t tangente in A alla parabola ha
coefficiente angolare dato da:
y ' (−2) = −2(−2) = 4
t : y − 5 = 4( x + 2) ⇒ y = 4 x + 13
Il centro della circonferenza da determinare è il
punto di intersezione tra l’asse delle ordinate e la
retta r passante per A perpendicolare a t:
1
1
1
9
mr = −
r : y − 5 = − ( x + 2) ⇒ y = − x +
4
4
4
2
−1
x = 0
C:
1
9
y = − 4 x + 2
x = 0
9
y = 2
Il raggio della circonferenza è: AC = 4 +
1
17
=
4
4
3
2
9
17
La circonferenza ha equazione: x + y − =
x 2 + y 2 − 9 y + 16 = 0
2
4
5) Scrivi l’equazione della parabola con asse parallelo all’asse delle ordinate, tangente in A(1;0) alla
retta t di coefficiente angolare 2 e passante per B(3;1). Determina sull’arco AB di parabola un
punto P in modo che risulti:
29
PH + PM =
4
essendo PH e PM le distanze di P dall’asse y e dalla retta y+4=0. (punti: 1,5)
2
y
3
La parabola ha equazione del tipo :
t
2
y = ax + bx + c , i parametri devono soddisfare alle
2
P
B
H
seguenti condizioni:
1
3
A
a = − 4
−3
−2
−1
1
2
3
A ∈ parabola
a + b + c = 0
−1
7
⇒ 9a + 3b + c = 1 ⇒ b =
B ∈ parabola
−2
2
m ( A) = 2
2 a + b = 2
t
11
−3
c = − 4
−4
M
3 2 7
11
y =− x + x−
−5
4
2
4
−6
Il punto P sull’arco AB della parabola ha coordinate
3
7
11
P k ; − k 2 + k − con 1 ≤ k ≤ 3
4
2
4
3
7
11
Quindi PH = k
PM = − k 2 + k − + 4
4
2
4
La relazione imposta dal problema diventa la seguente equazione:
⇒ k1 = 4 non accettabile
3
7
11
29
k − k2 + k − + 4 =
⇒ k 2 − 6k + 8 = 0
k 2 = 2 accettabile
4
2
4
4
x
4
5
6
7
5
Il punto P ha quindi le seguenti coordinate: P 2;
4
6) Traccia il grafico della funzione f ( x) = 2 − − 7 + 8 x − x 2 .
a) Determina il dominio D e l’insieme delle immagini Imf
b) Considerando f : D → Im f specifica se si tratta di una funzione iniettiva (giustifica la risposta).
(punti: 1,5)
Per tracciare l grafico della funzione si può ignorare il
5
modulo e poi ribaltare rispetto all’asse x le parti
negative.
4
y
y = 2 − − 7 + 8x − x 2
− 7 + 8x − x = 2 − y
3
2
2
1
x
1
2
3
4
5
6
7
8
−1
−2
4
− 7 + 8 x − x 2 ≥ 0
1 ≤ x ≤ 7
⇒ y ≤ 2
2 − y ≥ 0
2
2
2
2
x + y − 8 x − 4 y + 11 = 0 C (4;2) R = 3
x + y − 8 x − 4 y + 11 = 0
D = [1; 7] Im f = [0; 2]
Considerando f : D → Im f la funzione non è iniettiva, poiché esistono valori del codominio che
hanno più di una controimmagine.
y
4
7) Trova l’equazione della funzione
rappresentata.
a) Determina Dominio e insieme delle
immagini
b) Calcola l’immagine di 1
c) Calcola le controimmagini di 1
. (punti: 1,5)
3
2
1
x
−6
−5
La funzione rappresentata è definita a
tratti, in particolare in [− 6; − 2] è una
semicirconferenza di centro (-4; 2) e raggio 2
( x + 4) 2 + ( y − 2) 2 = 4 ⇒ ( y − 2) 2 = 4 − ( x + 4) 2
−4
−3
−2
−1
1
2
3
4
5
−1
Considerando la semicirconferenza con y ≤ 2 si ottiene y = 2 − 4 − ( x + 4) 2
y = 2 − − x 2 − 8 x − 12
mentre in [− 2; + ∞ ) è una semiparabola con asse orizzontale, vertice (-2; 2) passante per (2;4)
x + 2 = a ( y − 2) 2 imponendo il passaggio per il punto di coordinate (2;4) 2 + 2 = a (4 − 2) 2
a =1
x + 2 = ( y − 2) 2
Considerando la semiparabola con y ≥ 2 si ottiene y = 2 + x + 2
La funzione risulta quindi:
2 − − x 2 − 8 x − 12 − 6 ≤ x ≤ −2
y=
x>2
2 + x + 2
Con D = [− 6; + ∞ ) Im f = [0; + ∞ )
L’immagine di 1 è il valore che la funzione assume quando x=1, poiché in x=1 la funzione ha
come espressione la semiparabola, sostituisco il valore 1 nella seconda espressione
f (1) = 2 + 3
Le contrimmagini di 1 sono le eventuali x alle quali corrisponde y=1; dal grafico si osserva che
ciò si verifica per 2 valori sulla semicirconferenza che si possono trovare risolvendo:
1 = 2 − − x 2 − 8 x − 12
− x 2 − 8 x − 12 = 1
x 2 + 8 x + 13 = 0
x = −4 ± 3
5