Funzioni goniometriche per angoli di 30°, 60°, 45°
pag.1 di 3
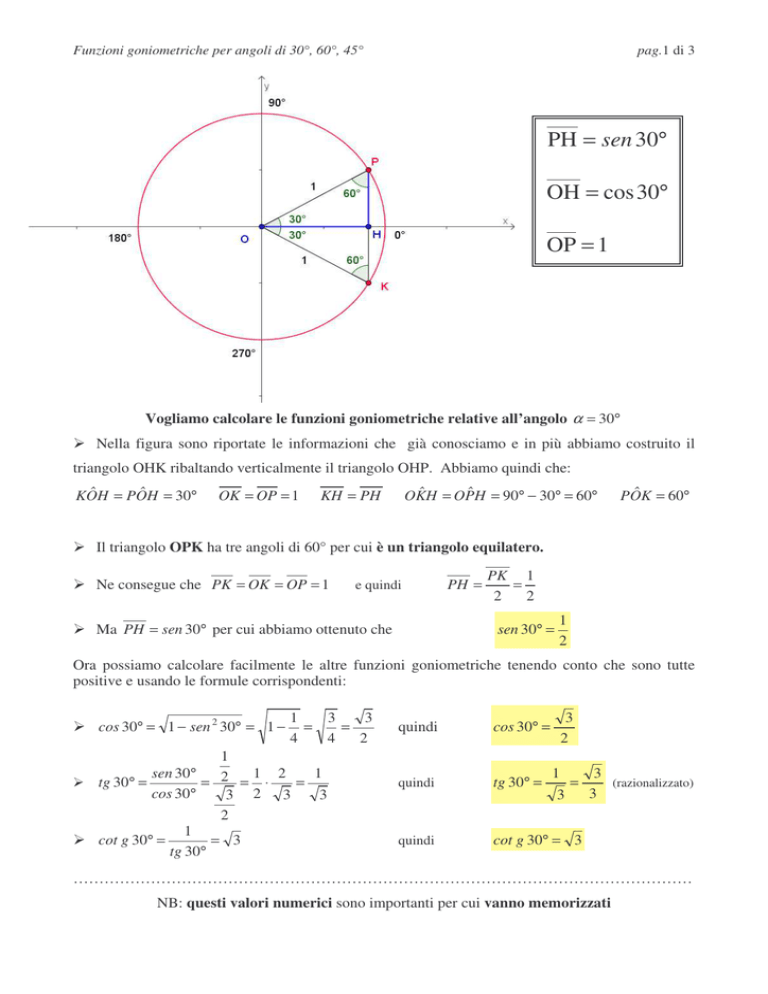
PH = sen 30°
OH = cos 30°
OP = 1
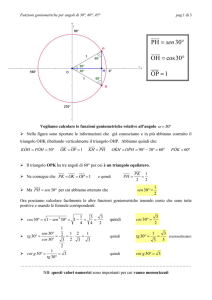
Vogliamo calcolare le funzioni goniometriche relative all’angolo α = 30°
Nella figura sono riportate le informazioni che già conosciamo e in più abbiamo costruito il
triangolo OHK ribaltando verticalmente il triangolo OHP. Abbiamo quindi che:
KÔH = PÔH = 30°
OK = OP = 1
KH = PH
OK̂H = OP̂H = 90° − 30° = 60°
PÔK = 60°
Il triangolo OPK ha tre angoli di 60° per cui è un triangolo equilatero.
Ne consegue che PK = OK = OP = 1
e quindi
PH =
PK 1
=
2
2
sen 30° =
Ma PH = sen 30° per cui abbiamo ottenuto che
1
2
Ora possiamo calcolare facilmente le altre funzioni goniometriche tenendo conto che sono tutte
positive e usando le formule corrispondenti:
cos 30° = 1 − sen 2 30° = 1 −
1
3
3
=
=
4
4
2
1
sen 30°
1 2
1
tg 30° =
= 2 = ⋅
=
cos 30°
3 2 3
3
2
1
cot g 30° =
= 3
tg 30°
3
2
quindi
cos 30° =
quindi
tg 30° =
quindi
cot g 30° = 3
1
3
=
3
(razionalizzato)
3
…………………………………………………………………………………………………………
NB: questi valori numerici sono importanti per cui vanno memorizzati
Funzioni goniometriche per angoli di 30°, 60°, 45°
pag.2 di 3
PH = sen 60°
OH = cos 60°
OP = 1
Vogliamo calcolare le funzioni goniometriche relative all’angolo α = 60°
Nella figura sono riportate le informazioni che già conosciamo e in più abbiamo costruito il
triangolo KHP. Abbiamo che:
180° − POˆ K 180° − 60°
KP = OP = 1 quindi OPˆ K = OKˆ P =
=
= 60°
2
2
Il triangolo OPK allora ha tre angoli di 60° per cui è un triangolo equilatero.
Ne consegue che OK = PK = OP = 1
e quindi
OH =
OK 1
=
2
2
cos 60° =
Ma OH = cos 60° per cui abbiamo ottenuto che
1
2
Ora possiamo calcolare facilmente le altre funzioni goniometriche tenendo conto che sono tutte
positive e usando le formule corrispondenti:
sen 60° = 1 − cos 2 60° = 1 −
1
3
3
=
=
4
4
2
3
sen 60°
3 2
tg 60° =
= 2 =
⋅ = 3
1
cos 60°
2 1
2
1
1
cot g 60° =
=
tg 60°
3
3
2
quindi
sen 60° =
quindi
tg 60° = 3
quindi
cot g 60° =
1
3
=
3
3
NB: questi valori numerici sono importanti per cui vanno memorizzati
E’ importante notare che con 60° si sono ricavati gli stessi valori ottenuti per 30° con la
differenza che si scambiano tra loro i valori di seno e coseno e quelli di tangente e cotangente.
Funzioni goniometriche per angoli di 30°, 60°, 45°
pag.3 di 3
PH = sen 45°
OH = cos 45°
OP = 1
Vogliamo calcolare le funzioni goniometriche relative all’angolo α = 45°
Il triangolo OPH è un triangolo rettangolo e isoscele (avendo gli angoli acuti entrambi di 45°)
Poniamo allora x = OH = PH (in questo caso x è positivo).
Il teorema di Pitagora applicato al triangolo rettangolo OHP ci permette di scrivere:
2
2
OH + PH = OP
x2 =
1
2
2
quindi
→
quindi
→
x=
Siccome OH = cos 45°
2
sen 45°
tg 45° =
= 2 =1
cos 45°
2
2
1
2
x 2 + x 2 = 12
quindi
→
quindi
→ 2 x 2 = 1
x = OH = PH =
PH = sen 45° abbiamo ricavato:
ne consegue poi:
1
2
=
2
2
cos 45° = sen 45° =
2
2
tg 45° = cot g 45° = 1
…………………………………………………………………………………………………………
NB: questi valori numerici sono importanti per cui vanno memorizzati