0.1
Relazione fondamentale della trigonometria
b Ricordando le definizioni di seno e
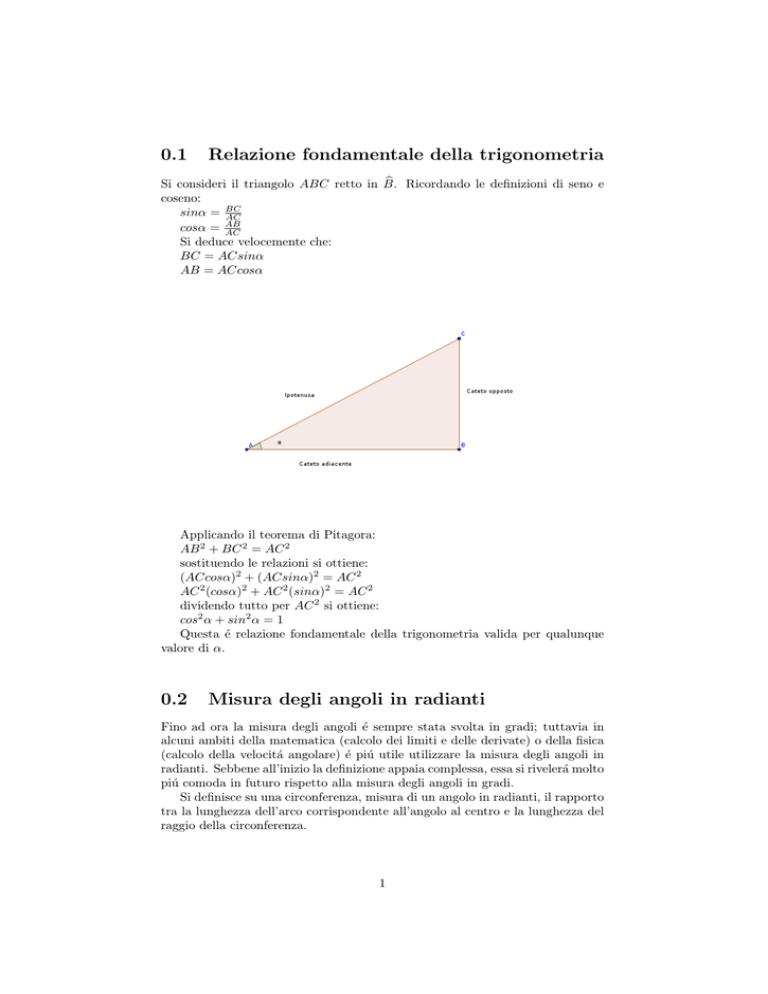
Si consideri il triangolo ABC retto in B.
coseno:
sinα = BC
AC
cosα = AB
AC
Si deduce velocemente che:
BC = ACsinα
AB = ACcosα
Applicando il teorema di Pitagora:
AB 2 + BC 2 = AC 2
sostituendo le relazioni si ottiene:
(ACcosα)2 + (ACsinα)2 = AC 2
AC 2 (cosα)2 + AC 2 (sinα)2 = AC 2
dividendo tutto per AC 2 si ottiene:
cos2 α + sin2 α = 1
Questa é relazione fondamentale della trigonometria valida per qualunque
valore di α.
0.2
Misura degli angoli in radianti
Fino ad ora la misura degli angoli é sempre stata svolta in gradi; tuttavia in
alcuni ambiti della matematica (calcolo dei limiti e delle derivate) o della fisica
(calcolo della velocitá angolare) é piú utile utilizzare la misura degli angoli in
radianti. Sebbene all’inizio la definizione appaia complessa, essa si rivelerá molto
piú comoda in futuro rispetto alla misura degli angoli in gradi.
Si definisce su una circonferenza, misura di un angolo in radianti, il rapporto
tra la lunghezza dell’arco corrispondente all’angolo al centro e la lunghezza del
raggio della circonferenza.
1
αRAD =
BC
R
A questo punto si consideri come angolo l’intero angolo giro che avrá come
arco corrispondente la lunghezza dell’intera circonferenza. La misura in radianti
dell’angolo giro sará:
αGIRO = 2πR
R = 2π
L’angolo giro misura quindi 2π radianti, l’angolo piatto, ossia la sua metá
misura quindi π radianti.
Con il medesimo ragionamento é possibile completare la tabella sottostante:
α[circ ]
0◦
30◦
45◦
60◦
90◦
120◦
135◦
150◦
180◦
210◦
225◦
240◦
270◦
300◦
315◦
330◦
360◦
α[rad]
0
π
6
π
4
...
...
...
...
...
...
...
...
...
...
...
...
...
...
2












