ISTITUTO TECNICO STATALE COMMERCIALE E PER GEOMETRI
“ A. MARTINI ” Castelfranco Veneto (TV)
IV A mercurio
2 ottore 2008
Docente: Daniele De Pieri
Funzioni goniometriche
1.
2.
3.
4.
5.
6.
7.
8.
9.
Trigonometria
Misura degli angoli e cerchio trigonometrico
Definizione di seno, coseno, tangente
Identità fondamentali
Valori delle funzioni circolari
Formule trigonometriche
Applicazioni della trigonometria
Equazioni goniometriche
Disequazioni goniometriche
1. Trigonometria
La parola trigonometria è composta da tre parole greche: τρί (tre) γωνία (angolo) µέτρον (misura).
Trigonometria dunque significa misura dei triangoli (τρίγωνον, triangolo).
La trigonometria ha avuto origine nella Grecia antica, dove venne impiegata per compiere calcoli notevoli come
la misura della circonferenza terrestre.
I greci infatti avevano compreso che la terra era di forma sferica e Eratostene di Cirene intorno al 200 a.C.
misurando l’inclinazione dei raggi solari stimò la circonferenza del nostro pianeta in 250.000 stadi.
Uno stadio valeva allora a circa 160 metri e dunque la stima di Eratostene corrispondeva a 40.000 Km.
Oggi sappiamo che la circonferenza della terra (prendendo come raggio una media tra poli e equatore) è di
40149 Km.
2. Misura degli angoli e cerchio trigonometrico
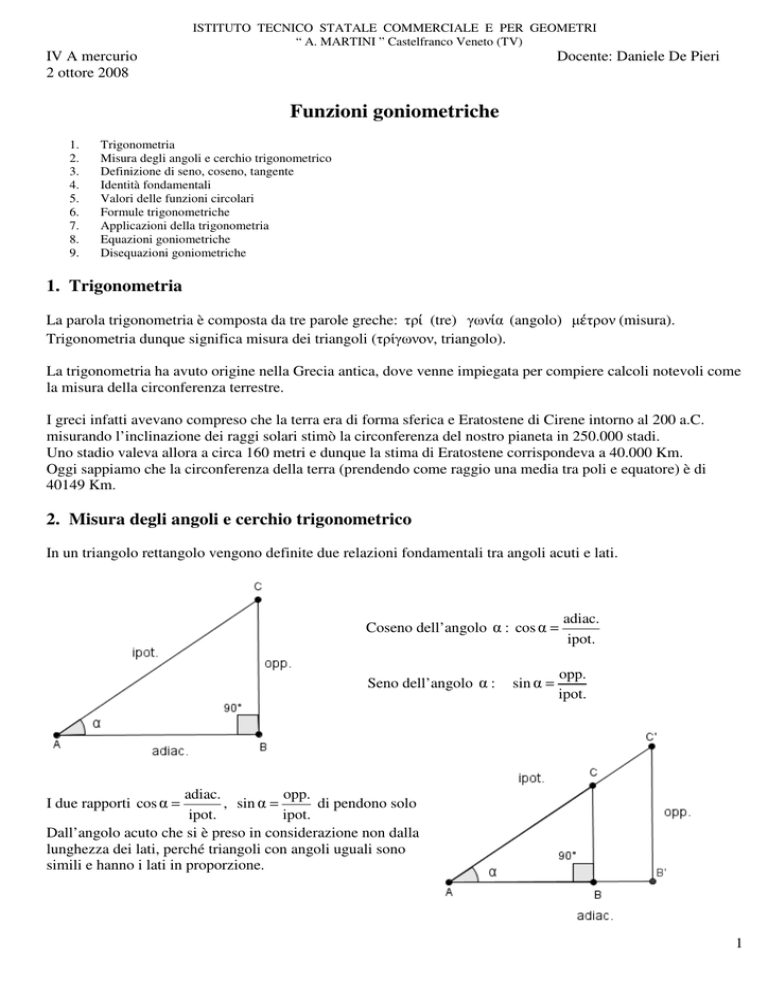
In un triangolo rettangolo vengono definite due relazioni fondamentali tra angoli acuti e lati.
Coseno dell’angolo α : cos α =
Seno dell’angolo α :
sin α =
adiac.
ipot.
opp.
ipot.
adiac.
opp.
, sin α =
di pendono solo
ipot.
ipot.
Dall’angolo acuto che si è preso in considerazione non dalla
lunghezza dei lati, perché triangoli con angoli uguali sono
simili e hanno i lati in proporzione.
I due rapporti cos α =
1
ISTITUTO TECNICO STATALE COMMERCIALE E PER GEOMETRI
“ A. MARTINI ” Castelfranco Veneto (TV)
IV A mercurio
2 ottore 2008
Docente: Daniele De Pieri
Considerando i due rapporti come funzioni dell’angolo acuto considerato, è opportuno ridefinirli in modo che
siano funzioni definite per ogni valore reale (e non solo per angoli tra 0° e 90°).
Le nuove definizioni sono espresse in termini di una circonferenza invece che di un triangolo.
Sia C la circonferenza: x 2 + y 2 = 1 , di raggio 1 e con centro nell’origine degli assi, sia A ( 0, 1) ∈ C .
Per ogni numero reale t , sia Pt il punto di C posto alla distanza t da A, misurata lungo C in verso
antiorario se t > 0 , in verso orario se t < 0 .
Ad esempio, poiché la misura della circonferenza è 2π il punto Pπ
punto A in senso antiorario: è il punto Pπ
2
2
si trova a un quarto della distanza C dal
(1, 0 ) .
Si dice misura in radianti dell’angolo al centro AOPt la lunghezza dell’arco sotteso da detto angolo.
Definizione di radiante
1 radiante è la misura dell’angolo al centro di una circonferenza che sottende una arco di lunghezza uguale al
raggio.
Tradizionalmente la misura degli angoli viene data in gradi (con base sessagesimale, base 60)
Per convertire i gradi in radianti si moltiplica per π / 180°
per convertire i radianti in gradi si moltiplica per 180° / π
3. Definizione di seno coseno tangente cotangente
Funzioni trigonometriche principali
sin t = PQ
t
cos t = OQ
tan t = TA
cot t = Pπ 2 C
2












