SOLUZIONE DEL QUESITO 7
TEMA DI MATEMATICA – ESAME DI STATO 2015
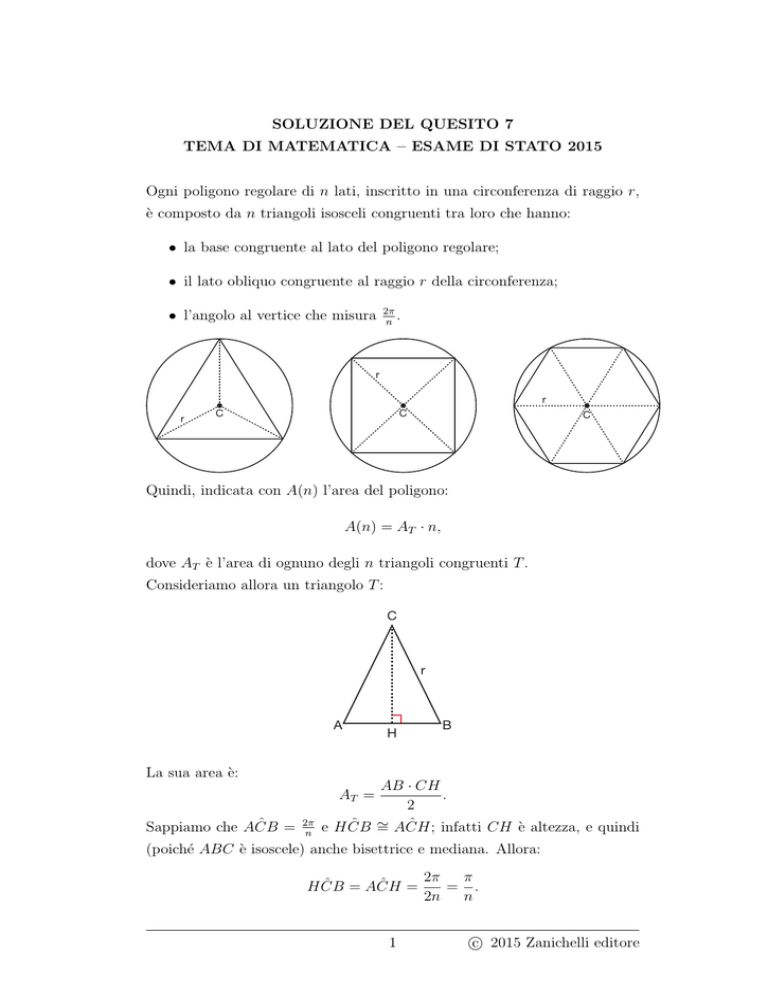
Ogni poligono regolare di n lati, inscritto in una circonferenza di raggio r,
è composto da n triangoli isosceli congruenti tra loro che hanno:
• la base congruente al lato del poligono regolare;
• il lato obliquo congruente al raggio r della circonferenza;
• l’angolo al vertice che misura
2π
.
n
r
r
r
C
C
C
Quindi, indicata con A(n) l’area del poligono:
A(n) = AT · n,
dove AT è l’area di ognuno degli n triangoli congruenti T .
Consideriamo allora un triangolo T :
C
r
A
La sua area è:
H
B
AB · CH
.
2
e H ĈB ∼
= AĈH; infatti CH è altezza, e quindi
AT =
Sappiamo che AĈB =
2π
n
(poiché ABC è isoscele) anche bisettrice e mediana. Allora:
H ĈB = AĈH =
1
π
2π
= .
2n
n
c 2015 Zanichelli editore
Scriviamo le lunghezze di base e altezza del triangolo T in funzione dell’angolo H ĈB.
La lunghezza di CH, cateto del triangolo rettangolo CBH, è:
π
CH = CB · cos(H ĈB) = r · cos .
n
La lunghezza di HB è invece:
π
HB = CB · sen(H ĈB) = r · sen .
n
Poiché HB = 12 AB:
π
AB = 2r · sen .
n
Dunque l’area del triangolo T è:
AB · CH
1
π
π
r2
2π
2
AT =
= · 2r · sen · cos =
· sen .
2
2
n
n
2
n
Pertanto, l’area del poligono regolare di n lati risulta:
A(n) =
n 2
2π
· r · sen .
2
n
Calcoliamo il limite di A(n) per n → +∞.
Osserviamo che, all’aumentare del numero dei lati, il poligono regolare tende
alla circonferenza in cui è inscritto.
C
C
C
È ragionevole aspettarci che il limite per n → +∞ dell’area A(n) sia l’area
del cerchio, cioè πr2 .
Svolgiamo il limite.
n 2
2π
n
2π
· r · sen
= r2 · lim
· sen .
n→+∞
n→+∞ 2
n→+∞ 2
n
n
Osserviamo che se n → +∞, allora:
lim A(n) = lim
2π
→ 0.
n
Quindi possiamo applicare il limite notevole:
senα
= 1.
α→0 α
lim
2
c 2015 Zanichelli editore
Moltiplicando e dividendo per π, otteniamo:
sen 2π
n
2π
· π · sen
= πr2 · 2πlim 2π n = πr2 · 1 = πr2 ,
n→+∞ 2π
n
→0
n
n
r2 · lim
che è il risultato che ci aspettavamo.
3
c 2015 Zanichelli editore