Tavola delle Funzioni Trigonometriche
Fabio Durastante
21 marzo 2010
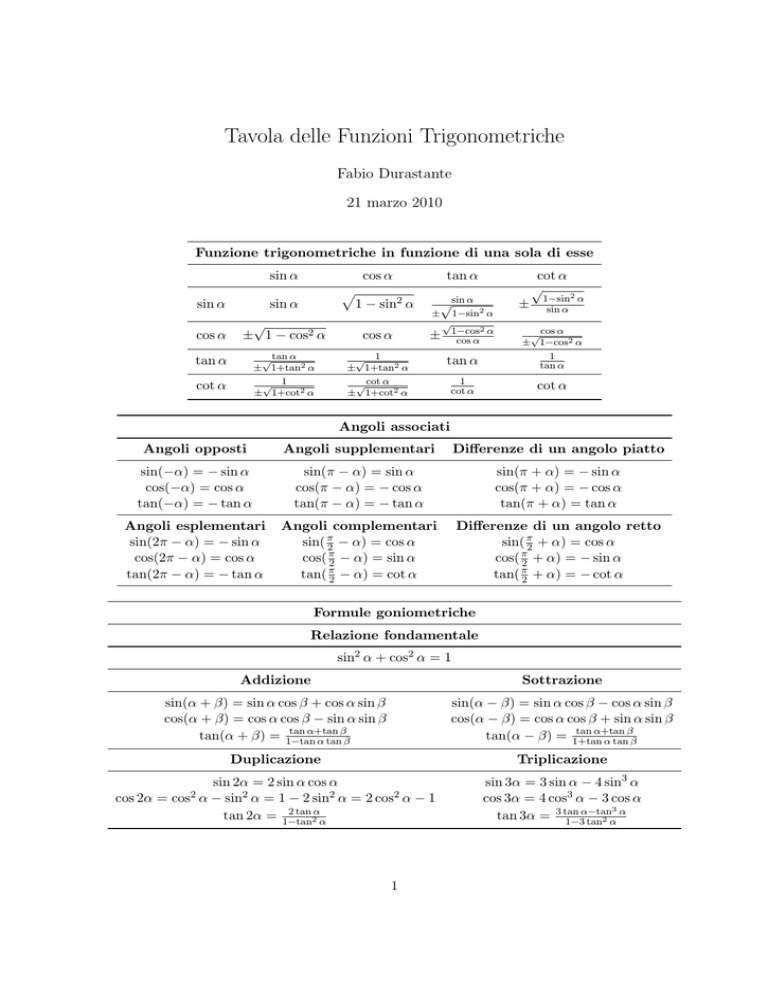
Funzione trigonometriche in funzione di una sola di esse
sin α
cos α
p
1 − sin2 α
sin α
sin α
cos α
√
± 1 − cos2 α
cos α
√ tan α
± 1+tan2 α
√ 1
± 1+cot2 α
√ 1
± 1+tan2 α
√ cot α
± 1+cot2 α
tan α
cot α
tan α
cot α
√
√sin α
1−sin2
±
√
α
1−cos2 α
cos α
±
1−sin2 α
sin α
tan α
√ cos α
± 1−cos2 α
1
tan α
1
cot α
cot α
±
Angoli associati
Angoli opposti
Angoli supplementari
Differenze di un angolo piatto
sin(−α) = − sin α
cos(−α) = cos α
tan(−α) = − tan α
sin(π − α) = sin α
cos(π − α) = − cos α
tan(π − α) = − tan α
sin(π + α) = − sin α
cos(π + α) = − cos α
tan(π + α) = tan α
Angoli esplementari
sin(2π − α) = − sin α
cos(2π − α) = cos α
tan(2π − α) = − tan α
Angoli complementari
sin( π2 − α) = cos α
cos( π2 − α) = sin α
tan( π2 − α) = cot α
Differenze di un angolo retto
sin( π2 + α) = cos α
cos( π2 + α) = − sin α
tan( π2 + α) = − cot α
Formule goniometriche
Relazione fondamentale
sin2 α + cos2 α = 1
Addizione
Sottrazione
sin(α + β) = sin α cos β + cos α sin β
cos(α + β) = cos α cos β − sin α sin β
tan α+tan β
tan(α + β) = 1−tan
α tan β
sin(α − β) = sin α cos β − cos α sin β
cos(α − β) = cos α cos β + sin α sin β
tan α+tan β
tan(α − β) = 1+tan
α tan β
Duplicazione
Triplicazione
cos 2α =
cos2 α
sin 2α = 2 sin α cos α
− sin2 α = 1 − 2 sin2 α = 2 cos2 α − 1
2 tan α
tan 2α = 1−tan
2α
1
sin 3α = 3 sin α − 4 sin3 α
cos 3α = 4 cos3 α − 3 cos α
α−tan3 α
tan 3α = 3 tan
1−3 tan2 α
Formule goniometriche
tan α2
formule di bisezione
q
α
sin α2 = ± 1−cos
q 2
α
cos α2 = ± 1+cos
2
q
α
sin α
= ± 1−cos
1+cos α = 1+cos α =
1−cos α
sin α
Prostaferesi
Werner
p−q
sin p + sin q = 2 sin p+q
2 cos 2
p−q
sin p − sin q = 2 sin 2 cos p+q
2
p−q
cos p + cos q = 2 cos p+q
cos
2
2
p−q
cos p − cos q = −2 sin p+q
2 sin 2
sin α sin β = 21 [cos(α − β) − cos(α + beta)]
cos α cos β = 12 [cos(α + β) + cos(α − beta)]
sin α cos β = 12 [sin(α + β) + cos(α − beta)]
Formule parametriche. Posto t = tan α2 allora:
2t
1 + t2
1 − t2
cos α =
1 + t2
sin α =
Teoremi sui triangoli. Dato un triangolo qualsiasi di angoli α,β,γ, con a opposto ad α, b opposto
a β e c opposto a γ sussistono le seguenti relazioni:
Triangoli rettangoli: 1
b = a sin β b = a cos γ b = c tan β b = c cot γ
c = a cos β c = a sin γ c = b tan γ c = b cot β
Teorema dei seni: 2
a
b
c
=
=
= 2r
sin α
sin β
sin γ
Teorema dei coseni (o di Carnot):
c2 = a2 + b2 − 2ab cos(γ)
b2 = a2 + c2 − 2ac cos(β)
a2 = b2 + c2 − 2bc cos(α)
Teorema delle tangenti:
tan α−β
a−b
2
=
α+β
a+b
tan 2
1
2
Formule per α retto.
r è il raggio della circonferenza circoscritta al triangolo.
2
Angoli notevoli
Angolo
Funzione goniometrica
α Gradi
0◦
α Radianti
0
9◦
π
20
15◦
π
12
π
10
π
8
π
6
π
5
π
4
3π
10
π
3
2π
5
5π
12
π
2
18◦
22◦ 300
30◦
36◦
45◦
54◦
60◦
72◦
75◦
90◦
√
sin α
0√
√
√
3+ 5− 5− 5
4
√ √
6− 2
4
√ √
5− 1
√ 4√
2− 2
2
1
√ 2 √
10−2 5
√4
2
2
√ √
5+ 1
√4
3
√ 2 √
10+2 5
√ 4√
6+ 2
4
√
1
cos α
1√
√
√
3+ 5+ 5− 5
4
√ √
6+ 2
√ 4 √
10+2 5
√ 4√
2+ 2
√2
3
2
√
5+1
√4
2
√ 2 √
10−2 5
4
1
2
√ √
5− 1
√ 4√
6− 2
4
0
3
tan α
√0
√
4− √10+2 5
5−1
√2 −
√
3
√
25−10 5
5
√
2√− 1
3
3
p
√
5−2 5
√ 1
√
25+10 5
√5
3
p
√
5+2 5
√
2+ 3
@
cot α
@
√
√ 5−1 √
4− 10+2 5
√
2+ 3
p
√
5+2 5
√
2+1
√
√ 3√
25+10 5
5
1
p
√
5−
2 5
√
√
3
3 √
25−10 5
5√
2− 3
0
Grafici delle funzioni trigonometriche
Funzione Seno
Funzione Arcoseno
Funzione Coseno
Funzione Arcocoseno
Funzione Tangente
Funzione Arcotangente
4












