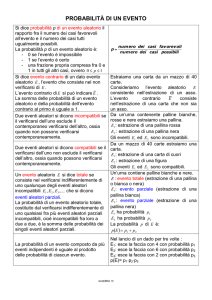
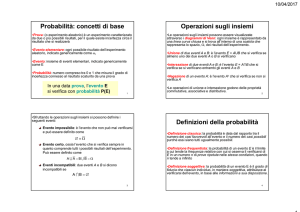
OSSERVAZIONI TEORICHE
Lezione n. 4
Finalità: Sistematizzare concetti e definizioni.
Verificare l’apprendimento.
Metodo: Lettura delle “OSSERVAZIONI” e risoluzione della scheda di
“verifica delle conoscenze concettuali”.
Materiali didattici: Schede individuali.
Riflessione collettiva
Dopo aver proposto l’argomento ai ragazzi con vari approcci, si sono
ordinate le idee enunciando le definizioni matematiche.
Per questo momento teorico si è dato ai ragazzi il materiale opportunamente preparato, cioè le “OSSERVAZIONI”, contenente esempi, definizioni e
regole matematiche sui concetti di probabilità, di eventi equiprobabili, di frequenza assoluta e relativa.
La lezione si è svolta leggendo, in classe, tale materiale e confrontando
di volta in volta la teoria con gli esercizi pratici svolti precedentemente; di
supporto è stato il libro di testo (G. Flaccavento Romano, Conoscere l’algebra,
Milano, Fabbri Editori, 1993).
Il momento teorico è stato motivo di discussione e di confronto fra i
ragazzi e l’insegnante.
In tale discussione si è chiesto loro di portare degli esempi sui vari tipi di
eventi considerati e si è notato l’incapacità di trovare esempi di eventi impossibili indipendenti dalle condizioni al contorno. I loro esempi sono stati del
tipo: “…è impossibile che oggi nevichi”, “…è impossibile che oggi succeda qualcosa a Potenza”, “…oggi è impossibile uscire prima da scuola”, cioè situazioni
che non è detto che non si verificheranno.
Durante la lezione si è utilizzato il vocabolario per definire il significato
di alcune parole. Infatti interessanti sono stati i confronti fatti tra i termini
“proverbio” e “detto”, da cui si è evinto che il proverbio è un detto ma che il
detto ha anche altri significati; e quello tra i termini “casuale” e “aleatorio”, da
cui si è osservato la comune dipendenza dalla parola “caso”.
Chiariti questi primi concetti è stato possibile proporre degli esercizi per
46
casa in modo da far assimilare il nuovo argomento. Questi richiedevano il riconoscimento tra i vari tipi di evento e la loro correzione è stata positiva, anche
se gli errori non sono mancati soprattutto nella valutazione degli eventi impossibili, cosa che è stata già notata nella precedente discussione in classe.
A conclusione dell’argomento ai ragazzi si è proposto una scheda di verifica individuale da compilare in classe, composta di quattro domande, a
risposta multipla, inerenti agli argomenti svolti nelle lezioni precedenti; per
tale prova è stato concordato un tempo di dodici minuti.
La correzione della scheda ha evidenziato che il concetto di evento aleatorio e l’intervallo di definizione della probabilità sono stati ben compresi dai
ragazzi, qualche interpretazione sbagliata si è presentata sulla definizione di
probabilità. Infatti una ragazza, alla domanda: “Che cos’è la probabilità?”, ha
risposto: “…è il grado di incertezza che abbiamo circa la verità di un’affermazione” perché ha ritenuto che il valore della fiducia sia uguale ed opposto al valore dell’incertezza. Da ciò si è evinto che il concetto poco chiaro è stato quello
della valutazione della probabilità che è stata intesa non come strumento matematico finalizzato a fornire maggiori certezze nella stima della previsione di un
evento, ma come valore di incertezza. All’ultima domanda riguardante l’equiprobabilità di due o più eventi aleatori solo quattro ragazzi hanno sbagliato
totalmente la risposta definendo equiprobabili due eventi con probabilità
diversa, tra le risposte esatte particolarmente interessante è stata quella di un
alunno, che ha osservato: “…due eventi aleatori o casuali sono equiprobabili
anche se sono ambedue certi o impossibili”. Ciò ha dimostrato come il ragazzo
abbia fatto proprio il concetto, rielaborandolo secondo il suo punto di vista.
Osservazioni critiche
Dopo la prima verifica si è potuto valutare il lavoro svolto, osservando
con stupore, l’impegno e l’interesse che i ragazzi hanno mostrato verso tale
argomento. Si è notato che gli esercizi pratici hanno favorito la loro attenzione e partecipazione alla lezione, mentre gli esempi hanno stimolato la loro
curiosità per saperne sempre di più sulla probabilità.
Dalle reazioni dei ragazzi si è intuito che la scelta didattica operata nella
compilazione delle prime schede ha favorito il grado di apprendimento prefissato, pertanto si è confermata l’importanza dell’interazione alunni-insegnante.
47
Scheda 4
Osservazioni n.1
Da queste prime osservazioni possiamo trarre alcune conclusioni:
a) Quello che facciamo sono delle “previsioni” e non delle “predizioni”.
Cioè facciamo delle previsioni circa il verificarsi di un evento futuro
sulla base delle conoscenze e delle informazioni di cui disponiamo
(RACCOLTA DATI). Si tratta di usare il nostro ragionamento e la
nostra memoria, non di tirare ad indovinare.
“Predire il futuro è più di astrologi e maghi”.
b) Queste previsioni riguardano eventi futuri quando siamo “in condizioni di incertezza”. Vengono esclusi i casi i cui siamo “sicuri” o che
l’evento si verificherà o che l’evento non si verificherà.
REGOLA
La probabilità studia le previsioni che possiamo fare circa il verificarsi di
eventi futuri quando siamo in condizioni di incertezza.
c) La probabilità del verificarsi di un evento futuro è compresa tra “0”
(probabilità dello 0%), se esso è del tutto impossibile, e “1” (probabilità del 100%), se esso è del tutto sicuro.
0 ≤ p(E) ≤ 1
d) Un evento futuro per il quale possiamo solo esprimere una valutazione di probabilità, cioè che non è né sicuro né impossibile, è denominato evento aleatorio, dal latino “alea” che significa dado. Quindi
un evento aleatorio viene anche detto “evento casuale”, per indicare
proprio le condizioni di incertezza in cui ci troviamo. Il verificarsi
dell’evento futuro dipende da fattori e circostanze che noi non possiamo determinare prima. Infatti lanciando un dado non siamo sicuri di quale risultato otterremo, ciò dipenderà dal caso.
REGOLA
Un evento aleatorio o casuale è un evento futuro incerto.
La probabilità di un evento aleatorio è sempre compresa tra 0 e 1.
Cioè:
0 ≤ p(E) ≤ 1
48
Osservazioni n.2
REGOLA
Due o più eventi casuali sono equiprobabili se, sulla base delle informazioni che abbiamo, possiamo assegnare a essi la stessa probabilità di verificarsi.
La valutazione di probabilità, o grado di fiducia che possiamo esprimere nei riguardi del verificarsi di un evento futuro incerto, deriva da due tipi
di informazioni:
a) Un’attenta analisi logica delle situazioni (scheda n°1 – caso dei proverbi)
b) Esperienza, cioè dall’aver accumulato informazioni relative al ripetersi degli eventi.
Questo tipo di informazione è studiato dalla statistica.
REGOLA (per eventi equiprobabili)
La probabilità di un evento è data dal rapporto tra il numero dei casi favorevoli al verificarsi dell'evento A e il numero dei casi possibili.
P(A)=
n(A)
n
REGOLA
La frequenza assoluta è il numero di volte con cui si presenta un dato risultato.
REGOLA
La frequenza relativa F dell’evento A è data dal rapporto tra il numero di
volte che l’evento si è verificato e il numero di prove effettuate.
F(A)=
n(A)
n
Osserviamo che: più aumenta il numero delle prove, più il valore della
frequenza F(A) si avvicina al valore della probabilità P(A).
49
Scheda n. 5
Verifica delle conoscenze concettuali
Scegli la risposta che ti sembra più giusta.
1 Un evento aleatorio o casuale è:
a) un evento passato verificato;
b) un evento futuro certo;
c) un evento futuro incerto;
d) un evento futuro impossibile.
2 Che cosa è la probabilità:
a) la predizione fatta da un mago sul futuro che ci attende;
b) il valore di verità di un’affermazione;
c) il grado di fiducia sul verificarsi di un evento futuro incerto;
d) il grado di incertezza che abbiamo circa la verità di un’affermzione.
3 La probabilità di un evento aleatorio:
a) è maggiore di 1;
b) è compresa tra 0 e 1;
c) è minore di 0;
d) è uguale a 1.
4 Due eventi aleatori o casuali sono equiprobabili se:
a) sulla base delle informazioni disponibili è possibile assegnare a
essi la stessa probabilità;
b) sono ambedue certi o impossibili;
c) uno di essi è certo e l’altro impossibile;
d) sulla base delle informazioni disponibili è possibile assegnare a
essi una probabilità diversa.
50