Ripasso su analitica e sistemi lineari
Abbiamo imparato a risolvere sistemi lineari di due o tre equazioni in due o tre incognite. In
geometria analitica si interpretano i risultati algebrici dal punto di vista geometrico.
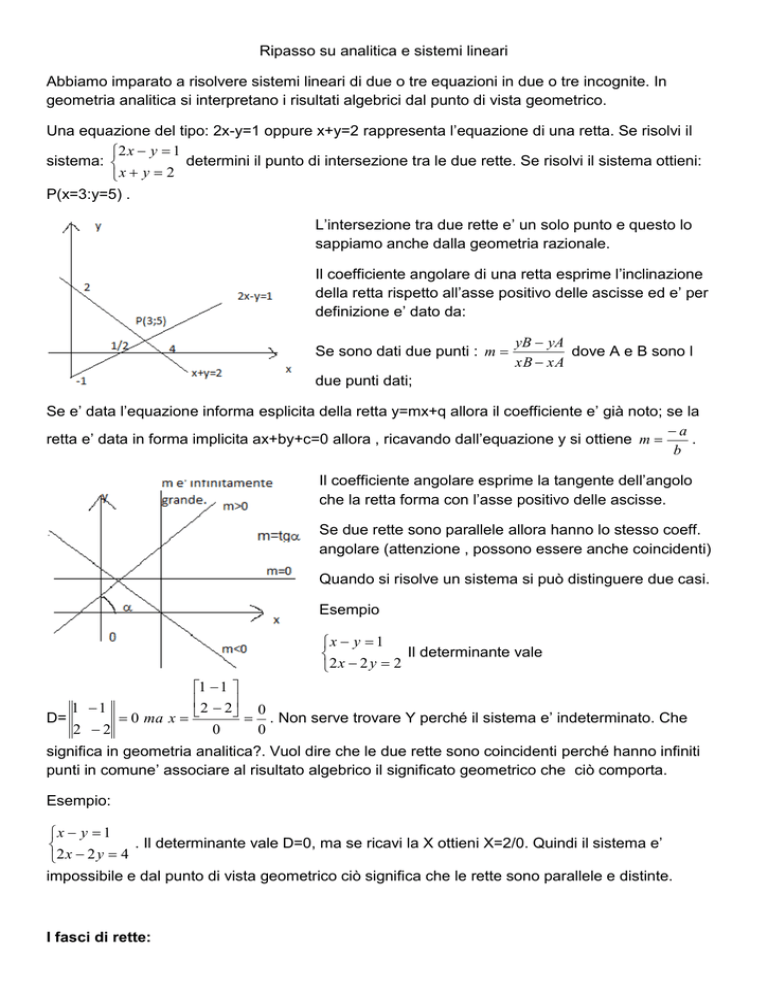
Una equazione del tipo: 2x-y=1 oppure x+y=2 rappresenta l’equazione di una retta. Se risolvi il
2 x y 1
sistema:
determini il punto di intersezione tra le due rette. Se risolvi il sistema ottieni:
x y 2
P(x=3:y=5) .
L’intersezione tra due rette e’ un solo punto e questo lo
sappiamo anche dalla geometria razionale.
Il coefficiente angolare di una retta esprime l’inclinazione
della retta rispetto all’asse positivo delle ascisse ed e’ per
definizione e’ dato da:
Se sono dati due punti : m
yB yA
dove A e B sono l
xB xA
due punti dati;
Se e’ data l’equazione informa esplicita della retta y=mx+q allora il coefficiente e’ già noto; se la
a
retta e’ data in forma implicita ax+by+c=0 allora , ricavando dall’equazione y si ottiene m
.
b
Il coefficiente angolare esprime la tangente dell’angolo
che la retta forma con l’asse positivo delle ascisse.
Se due rette sono parallele allora hanno lo stesso coeff.
angolare (attenzione , possono essere anche coincidenti)
Quando si risolve un sistema si può distinguere due casi.
Esempio
x y 1
Il determinante vale
2 x 2 y 2
D=
1 1
2 2
0 ma x
1 1
2 2
0
0
. Non serve trovare Y perché il sistema e’ indeterminato. Che
0
significa in geometria analitica?. Vuol dire che le due rette sono coincidenti perché hanno infiniti
punti in comune’ associare al risultato algebrico il significato geometrico che ciò comporta.
Esempio:
x y 1
. Il determinante vale D=0, ma se ricavi la X ottieni X=2/0. Quindi il sistema e’
2 x 2 y 4
impossibile e dal punto di vista geometrico ciò significa che le rette sono parallele e distinte.
I fasci di rette:
Un fascio di rette e’ un insieme di rette . Possono passare tutte per lo stesso punto (detto fascio
proprio) oppure possono essere rette parallele (detto fascio improprio).
Esempio 1:
Dato il fascio (a+1)x-(a-2)y-a+2=0 determina se esiste il punto comune a tutte le rette del fascio.
Un metodo e’ il seguente: assegna ad a un valore (esempio poni a=2) e ricava la retta:
Per a=2 si ha la retta 3x-1=0 cioè x=1/2 (retta parallela all’asse y);
Per a=3 si la retta: 4x-y-1=0.
Per stabilire l’esistenza del punto comune a tutte le rette mettiamo a sistema le due equazioni:
x 1/ 2
4 x y 1 .
Si ottiene P(1/2;1). Tutte le rette passano per il punto P(1/2;1)
Esempio 2
Dato il fascio di rette:2(a+1)x+(a+1)y-a+1=0 stabilisci la natura
del fascio.
Un secondo metodo consiste nel determinare il coefficiente
a 2(a 1)
m
2
b
(
a
1
)
angolare del fascio:
. Quindi tutte le rette del fascio , per ogni a, hanno
coefficiente angolare m=-2 e quindi sono parallele. Se calcoli m per il fascio dell’esempio 1 noti
che m dipende da a e quindi ogni retta ha un diverso coefficiente angolare.
Il fascio e’ improprio cioè le rette del fascio sono tutte
parallele.
Problemi sui fasci di rette:
E’ dato il fascio ax+(a-2)y-2a+1=0
1)Stabilisci se il fascio e’ proprio o improprio.
2)Determina il valore di a in modo che la retta del fascio:
a) passi per P(1;-2);
b)sia parallela alla retta y-2x+1=0;
c)formi con gli assi cartesiani un triangolo di area 1;
d)sia parallela all’asse x;
e)sia parallela all’asse y;
Soluzione:
1)Ho già risolto questo problema. Provaci.
2-a)Un punto appartiene ad una retta se le sue coordinate soddisfano la sua equazione.
Sostituisco alla x il valore 1 e alla y il valore -2. Ottengo:4a(1)+(a-2)(-2)-2a+1=0. Risolvi
l’equazione e trova a;
2-b)Due rette sono parallele se hanno lo stesso coefficiente angolare e termine noto diverso.
Quindi puoi procedere come segue:
m
4a
(coeff . ang . del fascio )
a2
m
(2)
(coeff . ang. della retta)
1
Quindi si ha:
4a
2 da cui a 2 / 3
a2
Puoi verificare che per a=2/3 le rette hanno termine noto diverso e quindi sono parallele e distinte.
2-c)L’area del triangolo la ottieni determinando i punti di intersezione della retta del fascio con gli
assi cartesiani.
x 0
x 0
y 0
Punto A :
(a 2) y 2a 1 0 da cui y 2a 1 . Punto B : x 2a 1
a2
4a
L’area del triangolo OAB deve valere 1 e quindi imposto l’equazione
1 2a 1 2a 1
) 1 a ?
(base x altezza diviso 2): (
2 4a a. 2
2-d)La retta e’ parallela all’asse delle ascisse se ha coefficiente angolare infinito. Determiniamo il
coefficiente angolare e ricorda che: una frazione e’ zero se il numeratore e’ zero; una frazione
ha valore infinito se il denominatore e’ zero.
Essendo m
4a
si ha una retta parallela all’asse x se m=0 da cui -4a=0 e a=0;
a2
2-e)La retta e’ parallela all’asse y se ha coefficiente infinito cioè se a-2=0 da cui a=2:
Questo e’ tutto ciò che devi sapere.
Risolvi il seguente esercizio e trova sul libro esempi simili per verificare la comprensione. Se hai
dei dubbi non esitare a chiedere all’insegnante.
Esempio da svolgere:
1)
2)
3)
4)
5)
6)
7)
Dato il triangolo A(3;3), B(-1;0), C(4;0).
Calcola area, perimetro, equazione dei lati, baricentro G;
Detti M e N i punti medi dei lati AB e AC scrivi l’equazione della retta MN. Verifica che MN
e’ parallela a BC e che MN=1/2AC.
Dimostra che BG=2GN (era nel compito);
Scrivi l’equazione della retta r passante per B e parallela a AC (usa l’equazione:
y-yA=m(x-xA);
Scrivi l’equazione della retta s passante per C e parallela ad AB;
Trova l’intersezione tra s e r;
Detto P il punto di intersezione tra r e s calcola l’area del triangolo PBC.
Problema sui fasci:
Dato l’insieme A ( x, y, a) 3 /( a 1) x ay a 3 , trova il valore di a affinche’ la retta
appartenete ad A:
1)passi per il punto P(-1;-2);
2)Passi per l’origine degli assi;
3)Sia parallela alla retta 2x-y+3=0;
4)Sia parallela all’asse x;
5)Sia parallela all’asse y;
6)Formi con gli assi un triangolo di area A=1;
7)Intersechi l’asse delle ordinate in un punto di ordinata y=3;
Intersechi l’asse delle ascisse in un punto di ascissa x=4;
Problema:
Sia A ( x, y, a) 3 / ax y a 0 (a 2) x ay 1 0 . Determina il valore di a affinché:
1) A ;
2)A sia costituito da un solo punto;
3)A sia costituito da tutti i punti di una retta.
(L’ insieme A e’ l’intersezione fra due equazioni. Chiedere che A sia vuoto vuol dire che il sistema
formato dalle due equazioni non ha soluzioni reali per il valore di a richiesto. Usa le matrici e il
metodo di Cramer. Se trovi il determinante , x e y puoi fare la discussione e lo abbiamo già fatto
più volte nel capitolo dedicato alla soluzione dei sistemi con discussione.. E’ solo il linguaggio
usato che può apparire diverso ma si chiedono le stesse cose. Cerca esercizi simile nel libro di
testo.
Esempio:
Siano: A ( x, y) 2 / x y 4 0 ; B ( x, y) 2 / y 3 0 ; C ( x, y) 2 / y 3x 12 0
a)Rappresenta graficamente gli insiemi su uno stesso piano cartesiano;
b)Determina A B C ;
c)Determina i vertici della figura geometrica che si costituisce la frontiera dell’insieme trovato ;
d)Determina l’area e il perimetro della frontiera.
Gli argomenti proposti sono gli stessi del compito. Verifica se sei in grado di affrontare una prova
simile nel prossimo compito.
Buon lavoro.












