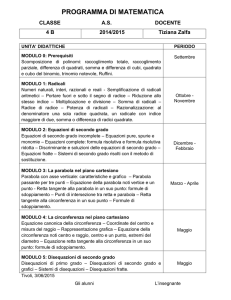
ANNO SCOLASTICO 2014-2015
CLASSE II E
DISCIPLINA: MATEMATICA
DOCENTE: Romio Silvana A.
PROGRAMMA SVOLTO A.S. 2014-2015
ALGEBRA
Ripasso sulle equazioni di I grado (tutti i tipi). Disequazioni intere (numeriche e letterali), fratte
(numeriche e letterali). Equazioni e disequazioni con il valore assoluto. Sistemi di disequazioni
letterali intere e fratte.
Sistemi di equazioni lineari con 2 incognite: metodi di risoluzione (sostituzione, confronto,
riduzione e Cramer). Gradi di libertà. Problemi risolvibili con i sistemi lineari.
Numeri reali. Numeri irrazionali: differenza tra numeri razionali e numeri irrazionali. Radicali
aritmetici e algebrici: proprietà e operazioni. Semplificazione di espressioni con radicali. Riduzione
di radicali allo steso indice. Trasporto fuori e dentro i radicali. Potenza di radicali.
Razionalizzazione dei denominatori. Condizione di esistenza dei radicali. Equazioni con coefficienti
irrazionali.
Equazioni di 2 grado numeriche o letterali, intere. Risoluzione via completamento del quadrato.
Discriminante di una equazione di II grado. Proprietà delle soluzioni di una equazione di II grado.
Relazione tra radici e coefficienti di una equazione di II grado.
Scomposizione del trinomio di 2° grado. Regola di Cartesio. Equazioni parametriche. Equazioni
letterali e numeriche fratte di II grado. Sistemi di II grado. Sistemi simmetrici ed omogenei.
Equazioni di grado superiore al 2risolubili mediante fattorizzazione. Sistemi di equazioni di grado
superiore al primo.
Disequazioni di 2 grado numeriche intere. Disequazioni numeriche fratte.
Disequazioni di grado superiore al 2°.
Sistemi di disequazioni. Sistemi simmetrici.
Equazioni irrazionali.
GEOMETRIA ANALITICA
Il piano cartesiano. Distanza tra due punti. Coordinate del punto medio.
Equazione della retta. Equazione della bisettrice del I/III quadranti e del II/IV. Proprietà
geometriche. Rette verticali ed orizzontali. Coefficiente angolare. Equazioni esplicita ed implicita.
Parallelismo e perpendicolarità. Retta passante per 2 punti. Distanza punto-retta. Fasci proprio e
improprio di rette. Esercizi e problemi.
Trasformazioni geometriche: Isometrie. Equazioni delle simmetrie assiali di asse verticale,
orizzontale, delle simmetrie centrali, delle traslazioni. Rotazione (senza equazioni). Applicazione
delle isometrie alle rette.
Equazione della parabola di asse verticale: la parabola come luogo geometrico. Dalla definizione
come luogo geometrico all’equazione. Determinazione dell’equazione della parabola dati tre punti,
un punto e il vertice, vertice e fuoco, vertice e direttrice, fuoco e direttrice. Intersezioni tra parabola
e retta, tra parabole, condizione di tangenza e rette tangenti. Isometrie applicate alla parabola.
Utilizzo del software GeoGebra per lo studio della geometria analitica.
Equazione delle omotetie con centro nell’origine. Proprietà. Confronto con le isometrie.
PROBABILITA’
Eventi e probabilità: definizioni (classica, frequentista, assiomatica, soggettiva)
Calcolo della probabilità di eventi semplici. Probabilità della somma logica di eventi. Probabilità
condizionata. Eventi indipendenti. Probabilità del prodotto logico di eventi. Estrazioni successive e
contemporanee. Applicazione alla valutazione dei test diagnostici.
GEOMETRIA SINTETICA
Quadrilateri: parallelogramma, rettangolo, rombo, quadrato, trapezio.
Isometrie: simmetrie assiali, simmetrie centrali, traslazioni, rotazioni e proprietà. Punti uniti,
insiemi uniti.
Utilizzo del software GeoGebra (free ware) per la risoluzione di problemi sui quadrilateri.
Trasformazioni geometriche del piano in se. Isometrie dal punto di vista sintetico.
Corrispondenza in un fascio di rette parallele. Corrispondenza di Talete.
Circonferenza e cerchio: corde, angoli al centro e angoli alla circonferenza.
Poligoni inscritti e circoscritti, poligoni regolari.
Poligoni equiscomponibili, teoremi di Pitagora e Euclide (I e II).
Omotetia: definizione, proprietà. Proporzionalità e teorema di Talete. Criteri di similitudine tra
triangoli. La similitudine nella circonferenza.
COMPITI (esercizi dal libro di testo in adozione e verifiche scritte svolte in classe)
i.- Da ogni capitolo svolto durante l’anno scolastico 2014/2015 si dovranno svolgere i Test dalle
Verifiche di fine capitolo. Gli esercizi dovranno essere svolti su un apposito quaderno giustificando
la risposta scelta (cioè, non basta indicare la risposta corretta) che sarà consegnato il giorno
dell’esame scritto oppure il primo giorno di lezione del prossimo A.S. Per il capitolo G8 si
dovranno svolgere solo i primi 5 quesiti del test.
ii.- Svolgere tutte le verifiche scritte (compresi i test) in fondo a questo documento.
N.B. Gli studenti promossi senza debito e senza “lettera di aiuto” possono svolgere il 50% degli
esercizi indicati. Si consiglia di svolgere i compiti in un apposito quaderno che sarà consegnato al
docente all’inizio del nuovo anno scolastico.
Pavia, 09/06/2015
L’insegnante:
FTO Silvana A. Romio
VERIFICA NOVEMBRE 2014
CLASSE = IIE – 10/11/2014
Nome e cognome dello studente = …...............................................................................................
Risolvere i seguenti esercizi e problemi ricordando di usare il buon senso e giustificando tutte
le risposte!!!
E1)
E2)
E3)
E4) Risolvere ciascuno dei seguenti sistemi lineari a 2 incognite scegliendo un metodo diverso
(cioè, non si può usare lo stesso metodo per risolvere 2 sistemi diversi)
a)
b)
E5) Per quale valore del parametro a il seguente sistema risulta impossibile? Giustificare la risposta
Problema 1: la terza parte della somma di due numeri interi consecutivi è minore di 7. Qual è il
maggior valore possibile dei due numeri?
Problema 2:
Considerare la retta passante per i punti A(-3,0) e B(0,2)
i.
ii.
iii.
iv.
v.
vi.
vii.
calcolare l’equazione della sua perpendicolare passante per l’origine delle coordinate O.
Chiamando C il punto di intersezione delle due rette, calcolare l’area del triangolo ACO; indicare
anche di che tipo di triangolo si tratta.
Calcolare l’area del triangolo AOB quindi quella del triangolo OCB.
Applicando una simmetria centrale di centro B, calcolare i trasformati dei vertici dei 2 triangoli AOB
e ACO, indicando il tipo di triangoli ottenuti e le loro aree
Calcolare l’equazione della retta trasformata della retta originale passante per i punti A e B.
Come risultano i segmenti AO’e AO? E i segmenti O’C’e OC? Giustificare le risposte
Rappresentare graficamente in un unico piano cartesiano.
VERIFICA DICEMBRE 2014 (interrogazione scritta)
Studente = ...................................................................
Classe = II E
Data = 15/12/2014
E1. Per quali valori del numero reale a esiste il radicale
A
Solo per a ≥ 0
B
Solo per a ≥ -2
C
Solo per a > -2
D
Solo per a ≥ 2
E
Per ogni valore di a
E2.
?
=
A
B
C
D
E
-9
3
-3
Nessuno dei precedenti
Giustificare la risposta
E3. Il risultato di
è
A
B
C
D
E
Nessuno dei precedenti
E4. Si consideri il sistema lineare
Indicare per quali valori del parametro a il sistema ammette una unica soluzione e per quali valori
invece non ne ammette alcuna. Giustificare la risposta.
E5. Cosa si intende per isometria? Indicare almeno un tipo di isometria e sue caratteristiche
principali descrivendo anche punti uniti ed insiemi uniti (se esistono).
E6. Senza eseguire calcoli risolvere la seguente disequazione
Giustificare la risposta
E7. Indicare i coefficienti angolari della retta r1 parallela e della retta r2 perpendicolare alla retta
passanti per il punto A(1,4). Trovare il punto di intersezione delle rette r1 ed r2. Giustificare le
risposte.
VERIFICA GENNAIO 2015
Studente = ...................................................................
Classe = II E
Data = 12/01/2015
Geometria Analitica
Dato il fascio di rette
mx-y-m+1=0
i.
ii.
iii.
iv.
v.
vi.
Determinare se è proprio o improprio
Se è proprio, trovare il suo centro A
Considerare le rette del fascio passanti per C(0,2) e O(0,0). Calcolare i punti F e G d’intersezione
delle suddette rette con la retta verticale passante per il punto B(-2,0)
Calcolare perimetro e area del triangolo AFG
Considerare la traslazione di vettore v(1,1) quindi il triangolo traslato A’F’G’. Calcolare perimetro e
area del nuovo triangolo (Hint: ricordare di non fare calcoli inutili…)
Chiamando H il punto d’intersezione del lato AF del primo triangolo con il lato F’G’ del triangolo
traslato, calcolare l’area del quadrilatero F’HAA’. Di quale quadrilatero si tratta?
Radicali
Dopo aver determinato le condizioni di esistenza risolvere i seguenti radicali:
1.-
2.-
Eseguire le operazioni indicate supponendo verificate le condizioni di esistenza
3.-
4.-
Supponendo verificate le condizioni di esistenza, risolvere le seguenti espressioni portando fuori
dalla radice quando possibile
5.6.-
7.- Supponendo che i fattori che compongono i radicali siano positivi, risolvere la seguente
espressione
8.- Date una circonferenza di centro O e una sua corda AB, dopo aver costruito il punto medio M
della corda, scegliere su di essa due punti C e D equidistanti da M. Dimostrare che C e D sono
anche equidistanti da O.
VERIFICA FEBBRAIO 2015
CLASSE = II LE – Data = 23/02/2015
Studente = ............................................................................................................................................
Risolvere i seguenti esercizi e problemi ricordando di usare il buon senso!!!
E1) Semplificare e razionalizzare i denominatori
E2) Semplificare, determinando le CE
E3) Dopo aver scritto l’equazione in forma normale, risolverla utilizzando un qualsiasi
metodo
E4) Risolvere la seguente equazione determinandone il campo di esistenza:
E5) Per ogni condizione, determinare il valore del parametro k nell’equazione che la soddisfa
ricordando che le soluzioni devono essere reali
i.
Le radici sono uguali
ii.
Le radici sono opposte
iii.
Le radici sono reciproche
iv.
Una delle radici è uguale a
v.
La somma delle radici coincide con il loro prodotto
E6) Semplificare la seguente frazione algebrica determinando le condizioni di esistenza
E7) Problema
In una pizzeria, la pizza singola (diametro 25 cm) costa euro 3.50 mentre la pizza doppia (diametro
36 cm) costa euro 7.
a) Quale scelta devono fare due amici per mangiare di più spendendo meno?
b) Che diametro dovrebbe avere la pizza piccola affinché la scelta sia ugualmente conveniente
per i due amici?
VERIFICA MARZO 2015
CLASSE = II LE – Data = 23/03/2015
Studente = ............................................................................................................................................
E1.- Considerare una circonferenza di centro O e i punti P e Q, fuori di essa, equidistanti da O.
Tracciati i segmenti di tangente condotti da P e da Q alla circonferenza, dimostrare che sono
congruenti.
E2.- Disegnare un triangolo rettangolo circoscritto a una circonferenza. Dimostrare che il diametro
della circonferenza è congruente alla differenza fra la somma dei cateti e l’ipotenusa.
E3.- Enunciare e dimostrare la condizione necessaria e sufficiente affinché un quadrilatero sia
iscrivibile in una circonferenza.
E4.- Dopo aver definito il concetto di baricentro di un triangolo dimostrarne l’esistenza
VERIFICA MAGGIO 2015
CLASSE = II E – Data = 18/05/2014
Studente = ............................................................................................................................................
Risolvere i seguenti esercizi e problemi ricordando di usare il buon senso!!! Giustificare tutte
le risposte.
E1) Risolvere le seguenti disequazioni
D1)
D2)
E2) Risolvere i seguenti sistemi
S1) (achtung baby!!! Fare solo i calcoli necessari dopo aver analizzato attentamente le
espressioni!!!!)
S2)
Problema :
i. Calcolare l’equazione della parabola avente vertice V(-1/4,-25/8) e fuoco F(-1/4,-3)
ii.
Scrivere l’equazione dell’asse di simmetria della parabola
iii.
Calcolare i punti d’intersezione della parabola con l’asse x (P e Q dove Q sta a destra di P) e
con l’asse y (I)
iv.
Trovare le tangenti alla parabola nel punto Q trovato precedentemente e nel punto R
appartenente alla parabola e di ascissa -1. Calcolare inoltre il punto T di intersezione tra
questa tangente (quella nel punto R) e l’asse x.
v.
Calcolare il punto S di intersezione delle tangenti calcolate nei punti R e Q
vi.
Calcolare l’area del triangolo TSQ e del suo simmetrico rispetto alla simmetria assiale di
asse x=1.
vii.
Calcolare l’equazione della parabola simmetrica alla parabola data nella simmetria di asse
x=1 considerata al punto precedente
viii.
Usando solo le equazioni della simmetria, calcolare il vertice V’, il fuoco F’, l’asse di
simmetria ed i vertici T’S’Q’ del trasformato del triangolo precedente. Calcolare il
perimetro del triangolo T’S’Q’
Geometria Euclidea:
Enunciare e dimostrare il teorema di Pitagora