Coseno, seno e π - mat.uniroma3

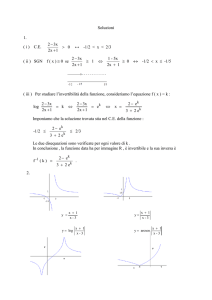
1
Università “Roma Tre” – L. Chierchia
Coseno, seno e π
(8/12/2016)
Qui daremo una presentazione analitica e autocontenuta della definizione e delle proprietà
fondamentali del coseno, del seno e di π.
Definizione 1 Per ogni x ∈ R poniamo

∞
2k
X

x2
x4
x6
x8
x10

k x

cos
x
:=
=
1
−
+
−
+
−
+ ···
(−1)


(2k)!
2
24 720 40320 3628800


k=0
(1)

∞

X

x2k+1
x3
x5
x7
x9
x11


sen
x
:=
(−1)k
=x−
+
−
+
−
+ ···


(2k + 1)!
6
120 5040 362880 39916800
k=0
Osservazione 2 (i) Le due serie in (1) convergono assolutamente per ogni1 x ∈ R e
cos 0 = 1
sen 0 = 0
cos(−x) = cos x
sen (−x) = − sen x .
(2)
(ii) Le formule (1) permettono di calcolare (con precisione arbitraria) il valore del seno e
coseno in qualunque punto x.
Ad esempio,
cos 2 =
4
X
(−1)k
k=0
22k
131
+r =−
+r ,
(2k)!
315
r :=
∞
X
(−1)k
k=5
22k
.
(2k)!
(3)
E ricordando che vale la stima2
rn (t) :=
∞ k
X
t
tn
<2
,
k!
n!
∀ n ∈ N0 , ∀ 0 < t ≤
k=n
n+1
,
2
(4)
si ha che
|r| <
∞
X
(4) 211
8
2k
= r10 (2) <
=
,
k!
10!
14175
k=10
e quindi3
− 0.417 < −
5903
841
< cos 2 < −
< −0.415 .
14175
2025
(5)
Studiamo il comportamento del seno e coseno “vicino” a x = 0:
1 Segue
dal criterio del rapporto o dal confronto con le serie iperboliche: | cos x| ≤ cosh |x|, | sin x| ≤ sinh |x|
(Esercizio 1).
2 Vedi formula (10) del file “La serie esponenziale”.
3 Esercizio 2.
2
Università “Roma Tre” – L. Chierchia
Lemma 3 Per ogni |x| ≤ 1 si ha
2
4
cos x − 1 + x ≤ x ;
2
12
4
7 2
| sen x| ≤ |x| ,
|1 − cos x| ≤
x ;
3
12
x2
1 − cos x 1 x2
sen x
− ≤
− 1 ≤
,
, (x 6= 0) .
x
3
x2
2
12
| sen x − x| ≤
|x|3
,
3
(6)
(7)
(8)
Dimostrazione Dalla definizione di seno e coseno e dalla (4) segue che, per |x| ≤ 1,
| sen x − x|
∞
∞
X
x2k+1 X |x|2k+1
= (−1)k
≤
(2k + 1)!
(2k + 1)!
k=1
≤
k=3
2
cos x − 1 + x 2
k=1
∞
X
|x|k
|x|3
|x|3
≤ 2
=
k!
6
3
(4)
∞
∞
X
x2k X x2k
(−1)k
= ≤
(2k)!
(2k)!
k=2
≤
k=2
∞
X
|x|k
k=4
k!
4
(4)
≤ 2
x
x4
=
.
4!
12
Da (6) segue che
4
x2
| sen x| = | sen x − x + x| ≤ | sen x − x| + |x| ≤ |x|
+ 1 ≤ |x|
3
3
2
2
2
x
x
1
7
x
≤ x2
+
=
x2 .
|1 − cos x| ≤ 1 − cos x − +
2
2
12 2
12
Infine (8) segue immediatamente da (6) dividendo per |x|.
Osservazione 4 (i) Da (6) segue che
lim sen x = 0 ,
x→0
lim cos x = 1 ,
x→0
(9)
ossia – ricordando (2) – che seno e coseno sono continue in 0. Le disuguaglianze (8) implicano
i seguenti limiti notevoli:
lim
x→0
sen x
=1,
x
1 − cos x
1
= .
2
x→0
x
2
lim
(10)
Teorema 5 (Formula di addizione per il coseno)
cos(x + y) = cos x cos y − sen x sen y ,
∀ x, y ∈ R.
(11)
3
Università “Roma Tre” – L. Chierchia
Dimostrazione Dalla definizione di coseno segue che
cos(x + y) = lim
N →∞
N
X
(−1)k
k=0
(x + y)2k
.
(2k)!
(12)
Ora, per ogni N ∈ N, si ha4
N
X
(−1)k
k=0
(x + y)2k
(2k)!
(i)
=
N
2k X
(−1)k X 2k j 2k−j
x y
(2k)! j=0 j
k=0
=
N
X
(−1)k
y 2k−j
j! (2k − j)!
j=0
k=0
=
2k
X
xj
1+
N
X
2k
X
xj
(−1)k
j=0
k=1
(ii)
=
1+
N
X
N
X xj y 2k−j
X
X xj y 2k−j
(−1)
+
(−1)k
j! (2k − j)!
j! (2k − j)!
0≤j≤2k
0≤j≤2k
k
k=1
(iii)
=
1+
N
X
=
k=0
h=0
k=1
h=0
k
N
k−1
X
X
X x2h+1
x2h y 2(k−h)
y 2(k−h)−1
k
k
(−1)
+
(−1)
(2h)! (2(k − h))!
(2h + 1)! (2(k − h) − 1)!
h=0
k=1
h=0
N
−1
k
k
X
X
X
x2h+1
y 2(k−h)+1
x2h y 2(k−h)
−
(−1)k
(−1)k
(2h)! (2(k − h))!
(2h + 1)! (2(k − h) + 1)!
(iv)
=:
AN − BN −1 .
k=0
j dispari
k
N
k−1
X
X
X x2h+1
x2h y 2(k−h)
y 2(k−h)−1
(−1)k
+
(−1)k
(2h)! (2(k − h))!
(2h + 1)! (2(k − h) − 1)!
N
X
=
k=1
j pari
k=1
N
X
y 2k−j
j! (2k − j)!
k=0
h=0
h=0
La tesi seguirà quindi dai limiti:
lim AN = cos x · cos y ,
N →∞
lim BN = sen x · sen y ,
N →∞
(13)
che, ora, andiamo a dimostrare. Infatti, discuteremo in dettaglio solo il limite di AN , essendo
la discussione per il limite di BN del tutto analoga (Esercizio 3∗ ).
4 (i):
segue dalla formula del binomio di Newton.
M
X
X
(ii): se I ⊂ R è un insieme finito, la notazione
ai significa, per definizione,
aij dove M è il numero di
i∈I
j=1
elementi di I e {ij | 1 ≤ j ≤ M } = I (con {ij } tale che ij 6= ij 0 se j 6= j 0 ).
(iii) nella prima somma poniamo j = 2h e nella seconda somma j = 2h + 1.
(iv): nella seconda somma su k facciamo prima il cambio di variabile k = n − 1 e poi risostituiamo n con k
(che è un cambio di indice muto).
4
Università “Roma Tre” – L. Chierchia
Scambiando l’ordine delle somme su k e h si ha5
AN
:=
N X
k
X
(−1)k
k=0 h=0
(i)
=
N X
N
X
(−1)k
h=0 k=h
=
N
X
(−1)h
h=0
(ii)
=
N
X
=
x2h y 2(k−h)
(2h)! (2(k − h))!
N
x2h X
y 2(k−h)
(−1)k−h
(2h)!
(2(k − h))!
k=h
(−1)h
h=0
(iii)
x2h y 2(k−h)
(2h)! (2(k − h))!
−h
2h N
X
x
(2h)!
(−1)j
j=0
y 2j
(2j)!
N
−h
2h N
X
X
y 2j
y 2j
h x
+
(−1)
(−1)j
(−1)
(2j)!
(2h)! j=0
(2j)!
j=0
N
X
j
h=1
=
N
N
N
X
X
y 2j
y 2j
x2h X
(−1)j
(−1)j
+
(−1)h
−
(2j)!
(2h)! j=0
(2j)!
j=0
=
N
N
N
N
X
X
X
y 2j
x2h X
y 2j
x2h
(−1)j
+
(−1)h
(−1)j
−
(−1)h
(2j)!
(2h)! j=0
(2j)!
(2h)!
j=0
h=1
h=1
(iv)
=
N
X
2h
(−1)h
h=0
=
N
X
x
(2h)!
N
X
N
X
(−1)j
j=N −h+1
h=1
2j
y
−
(2j)!
(−1)j
j=0
N
X
2h
(−1)h
h=1
x
(2h)!
N
X
y 2j (2j)!
N
X
(−1)j
j=N −h+1
y 2j
(2j)!
2j
(−1)j
j=N −h+1
y
(2j)!
N
y 2j x X
(−1)j
(−1)h
− RN
(2h)!
(2j)!
j=0
2h
h=0
dove
RN :=
N
X
(−1)h
h=1
x2h
(2h)!
N
X
(−1)j
j=N −h+1
y 2j
.
(2j)!
Il primo limite in (13) è dunque conseguenza del limite lim RN = 0. Ora, definiamo
N →∞
2
2
M := max{x , y , 1}
e si osservi che per ogni coppia di interi non negativi m ed n si ha6
m+n
1
2m+n
1 1
=
≤
.
m! n!
m
(m + n)!
(m + n)!
5 (i):
Se akh sono numeri,
N X
k
X
(14)
akh significa sommare tutti gli akh al variare delle coppie di interi (k, h)
k=0 h=0
tali che 0 ≤ h ≤ k ≤ N ; tali coppie possono essere elencate fissando 0 ≤ h ≤ N e, poi, prendendo k tale che
N X
N
X
h ≤ k ≤ N ; questo significa fare la somma
ahk .
h=0 k=h
(ii): nella seconda somma facciamo il cambio di variabile k = h + j.
(iii): la prima somma corrisponde al termine h = 0 nella riga precedente.
(iv): il termine con h = 0 corrisponde alla prima somma nella riga precedente.
6 Infatti,
per la formula del binomio di Newton, 2m+n = (1 + 1)m+n =
m+n
X k=0
maggiore di ogni suo addendo.
m + n
e tale somma è
m
5
Università “Roma Tre” – L. Chierchia
Segue:
|RN |
≤
N
X
x2h
(2h)!
h=1
≤
N
X
j=N −h+1
N
X
M 2N
y 2j
(2j)!
N
X
h=1 j=N −h+1
(14)
≤
N
X
M 2N
N
X
h=1 j=N −h+1
≤
N
X
M 2N
N
X
h=1 j=N −h+1
≤
(4M )2N
N
X
1
1
(2h)! (2j)!
22(h+j)
(2(h + j))!
24N
(2(N + 1))!
N
X
h=1 j=N −h+1
=
2N
(4M )
1
(N + 1)!
N
X
1
h
(N + 1)!
h=1
=
=
=
N (N + 1)
1
(4M )
(N + 1)!
2
1
1
(4M )2N
2
(N − 1)!
bN −1
a
,
dove a := 8M 2 , b := (4M )2 .
(N − 1)!
2N
E poiché lim bN /N ! = 0 per ogni b, si ha che lim RN = 0 e quindi che lim AN =
N →∞
N →∞
N →∞
cos x · cos y.
Osservazione 6 (i) Prendendo y = −x in (11) e ricordando (2) si ha che
cos2 x + sen2 x := (cos x)2 + ( sen x)2 = 1,
(15)
| cos x| ≤ 1 ,
(16)
da cui
| sen x| ≤ 1 ,
∀ x ∈ R.
Prendendo x = y in (11) otteniamo
cos 2x = cos2 x − sen2 x .
(17)
(ii) Da (11) e da (9) segue che il coseno è una funzione continua su tutto R: infatti, per ogni
x ∈ R,
lim cos z
z→x
=
(9)
(11)
lim cos(x + y) = lim cos x cos y − sin x sin y = cos x .
y→0
y→0
(iii) Da (ii) e dal teorema di permanenza del segno per funzioni continue segue che:
6
Università “Roma Tre” – L. Chierchia
se cos x0 6= 0 allora esiste δ > 0 tale che cos x · cos x0 > 0 (ossia cos x ha lo stesso segno di
cos x0 ) per ogni7 x ∈ [x0 − δ, x0 + δ].
Lemma 7 (“Teorema di esistenza degli zeri per funzioni continue”)
Sia f : [a, b] → R una funzione continua tale che f (a) > 0 > f (b) [oppure, f (a) < 0 < f (b)].
Allora esiste β ∈ (a, b) tale che f (β) = 0 e f (x) > 0 [oppure, f (x) < 0] per ogni x ∈ [a, β).
Dimostrazione Sia P := {d ∈ [a, b] : f (x) > 0 per ogni a ≤ x ≤ d}. Per ipotesi a ∈ P
e quindi P 6= ∅ e, chiaramente, b è un maggiorante di P . Sia β = sup P . Supponiamo (per
assurdo) che f (β) > 0: innanzitutto β < b (poiché f (b) < 0) e, per permanenza del segno,
segue che f (x) > 0 per x ∈ [β − δ, β + δ] ∩ [a, b] con un opportuno δ > 0 (e β + δ < b perché
f (b) < 0); quindi, β +δ ∈ P contraddicendo il fatto che β è un maggiorante di P . Supponiamo
ora (sempre per assurdo) che f (β) < 0: per permanenza del segno, seguirebbe che esiste δ > 0
tale che f (x) < 0 per x ∈ [β −δ, β +δ] (e β −δ > a poiché f (a) > 0): ma questo significherebbe
che β − δ < β è un maggiorante contraddicendo il fatto che β è l’estremo superiore di P .
Dunque f (β) = 0. Si osservi, infine, che a < β < b e che se a < y < β allora, (poiché β
è l’estremo superiore di P ) esiste d ∈ P tale che y < d < β, e dunque (definizione di P )
f (y) > 0.
Nel caso in cui f (a) < 0 < f (b) basta applicare il risultato precedente alla funzione continua
−f .
Corollario 8 Esiste β ∈ (1, 2) tale che cos β = 0 e cos x > 0 per ogni x ∈ [0, β).
Dimostrazione Poiché, per (5), cos 2 < 0 possiamo applicare il Lemma 7 a cos x ristretta
all’intervallo [0, 2]. Da (7) segue poi che | cos x − 1| ≤ 7/12 per |x| ≤ 1 e quindi cos x − 1 ≥
−7/12, ossia,
5
,
∀x ∈ [0, 1] ,
cos x ≥
12
il che implica che 1 < β.
Definizione 9 (Pi Greco) π := 2β dove β è il numero nel Corollario 8.
Proposizione 10 (Valori speciali)
cos
π
2
= 0, sen
π
2
= 1, cos π = −1, sen π = 0, cos 32 π = 0, sen 32 π = −1, cos 2π = 1, sen 2π = 0.
Dimostrazione Dalla definizione di π e dal Corollario 8 segue che cos π2 = 0; dunque da (15)
x
segue che | sen π2 | = 1. D’altra parte, da (8) segue che se 0 < x ≤ 1, sen
− 1 ≥ − 31 ossia
x
sen x
2
≥ 3 , e quindi, in particolare, sen x > 0 se 0 < x ≤ 1. Da (11) e dalla definizione di
x
π segue che, per ogni 0 ≤ x < π2 , cos π2 − x = sen π2 sen x; quindi se 0 < x < min{1, π2 },
sen x > 0 e cos π2 − x > 0, il che implica sen π2 = 1.
Da (17) segue che cos π = cos2 π2 − sen2 π2 = −1 e quindi, per (15), sen π = 0. Ancora da (17)
segue che cos 2π = cos2 π − sen2 π = 1 e quindi (da (15)) sen 2π = 0.
Infine, cos 32 π = cos(2π − π2 ) = cos 2π cos π2 + sen 2π sen π2 = 0, e −1 = cos π = cos 23 π − π2 =
cos 23 π cos π2 + sen 32 π sen π2 = sen 32 π.
7 Si noti che, in generale, se una proprietà P è vera in un intorno di x ∈ R significa che esiste r > 0 tale
0
che P è vera per ogni x ∈ (x0 − r, x0 + r); ma se prendiamo δ = r/2, P sarà vera anche in [x0 − δ, x0 + δ].
7
Università “Roma Tre” – L. Chierchia
Teorema 11 (Formula di addizione per il seno)
sen (x + y) = sen x cos y + cos x sen y ,
∀ x, y ∈ R.
(18)
Dimostrazione Da (11) e dalla Proposizione 10 segue immediatamente che
cos(x −
e anche (scrivendo cos x = cos (x − π2 ) +
π
2
sen x −
π
) = sen x
2
(19)
) che
π
= − cos x .
2
(20)
Quindi,
sen (x + y)
(19)
=
=
(20)
=
π
+y
2
π
π
cos x −
cos y − sen x −
sen y
2
2
cos x −
sen x cos y + cos x sen y .
Osservazione 12 Dalla formula di addizione per il seno (e da (2)) segue immediatamente la
continuità del seno su tutto8 R.
Dalle formule di addizione (Teoremi 5 e 11) seguono immediatamente molte altre relazioni
tra cui9 :
sen 2x = 2 sen x cos x ,
cos(x + π) = − cos x ,
(21)
sen (x + π) = − sen x ,
(22)
sen (x + 2π) = sen x ,
1 + cos 2x
cos2 x =
,
2
x + y
x − y
sen x + sen y = 2 sen
cos
,
2
2
x + y
x − y
cos x + cos y = 2 cos
cos
,
2
2
1
sen x sen y =
cos(x − y) − cos(x + y) ,
2
1
cos x cos y =
cos(x − y) + cos(x + y) ,
2
1
sen x cos y =
sen (x + y) + sen (x − y) ,
2
1
cos x sen y =
sin(x + y) − sen (x − y) .
2
(23)
cos(x + 2π) = cos x ,
1 − cos 2x
,
sen2 x =
2
(24)
(25)
(26)
(27)
(28)
(29)
(30)
Definizione 13
8 Esercizio
9 Esercizio
4.
5.
tan x
:=
cotan x
:=
sen x
,
cos x
cos x
,
sen x
∀ x 6=
π
+ kπ, k ∈ Z ,
2
∀ x 6= kπ, k ∈ Z .
(31)
(32)
8
Università “Roma Tre” – L. Chierchia
È facile dimostrare le seguenti relazioni10
cotan
π
− x = tan x ,
2
tan(x + π) = tan x ,
(34)
(35)
(36)
(37)
(38)
lim cotan x = +∞ ,
(39)
lim cotan x = −∞ .
(40)
x→0+
x→π−
6.
(33)
tan x = −∞ ,
lim
x→− π
2+
10 Esercizio
π
+ kπ, k ∈ Z ,
2
π
+ kπ, k ∈ Z ,
2
∀ x 6= kπ, k ∈ Z ,
∀ x 6=
cotan (x + π) = cotan x ,
tan x
=1,
lim
x→0
x
lim
tan x = +∞ ,
π
x→ 2 −
∀ x 6=