Corso di laurea in SCIENZE BIOLOGICHE
Prova scritta di:
ISTITUZIONI DI MATEMATICHE E FONDAMENTI DI BIOSTATISTICA
Data: 17.06.2013
Cognome e nome del candidato:
Numero di matricola:
I PARTE
Esercizio 1
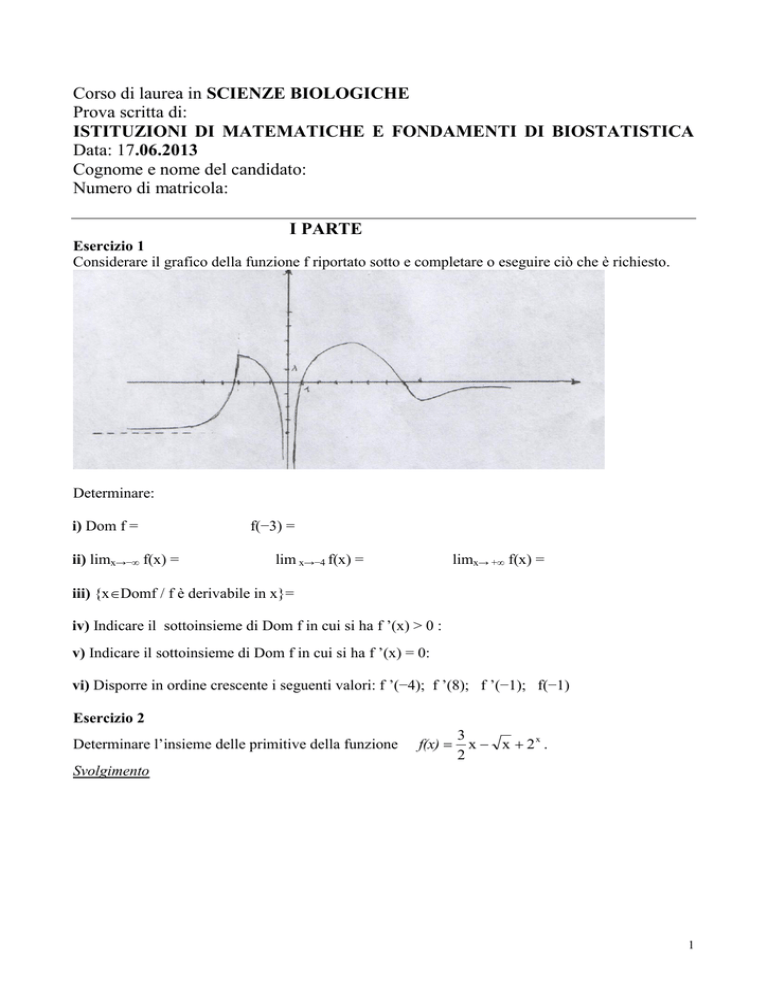
Considerare il grafico della funzione f riportato sotto e completare o eseguire ciò che è richiesto.
Determinare:
i) Dom f =
ii) limx→−∞ f(x) =
f(−3) =
lim x→−4 f(x) =
limx→ + f(x) =
iii) {xDomf / f è derivabile in x}=
iv) Indicare il sottoinsieme di Dom f in cui si ha f ’(x) > 0 :
v) Indicare il sottoinsieme di Dom f in cui si ha f ’(x) = 0:
vi) Disporre in ordine crescente i seguenti valori: f ’(−4); f ’(8); f ’(−1); f(−1)
Esercizio 2
Determinare l’insieme delle primitive della funzione
f(x)
3
x x 2x .
2
Svolgimento
1
Esercizio 3
Data la funzione f(x) = x 3 3x 15 , determinare la formula matematica della funzione derivata
e disegnare il grafico di f ’.
Grafico di f ’
Formula matematica
Esercizio 4
Utilizzare il metodo grafico per disegnare i grafici delle funzioni sotto indicate (indicare nel disegno
i valori numerici che caratterizzano gli eventuali punti di intersezione con gli assi o le equazioni
degli asintoti)
Svolgimento
ex
y
2
y 1 x 1
y 2senx
2
Esercizio 5
ln x
. Calcolare la derivata prima della funzione f e poi determinare f ’(1).
x2
x2
b) Sia g(x) =
. Calcolare la derivata prima della funzione g e poi determinare g’(e).
ln x
Svolgimento
a) Sia f(x) =
f ’(x) =
f ’(1) =
g’(x) =
g’(e) =
Esercizio 6
Calcolare i seguenti limiti, dopo aver prima disegnato i grafici delle funzioni considerate.
2
lim ( ) x
x 3
lim
x
3
x
lim senx
x π
lim x 2
x
lim log 1 x
x 0
3
Esercizio 7
In uno studio che esamina la causa di morte in soggetti affetti da asma grave, sono stati raccolti dati
su un campione di 10 pazienti pervenuti in ospedale con arresto respiratorio. La frequenza cardiaca,
misurata in battiti al minuto, dei dieci pazienti al momento dell’ammissione è stata la seguente:
150 150 40 136 120 150 167 150 125 120
a) Disegnare l’istogramma delle frequenze relative della distribuzione.
b) Caratterizzare la serie di osservazioni determinando media aritmetica, mediana e moda della
frequenza cardiaca.
Svolgimento
a)
b)
3
II PARTE
Esercizio 8
Calcolare l’area della regione di piano delimitata dall’asse x, dalla curva y = x3+1 e dalle rette di
equazione y = −x−1 ed x = 2. Rappresentare nel piano cartesiano la regione considerata.
Svolgimento
Fare la figura
Impostare il calcolo dell’area:
Calcolare il valore dell’area esplicitando i passaggi effettuati
4
Esercizio 9
Studiare la funzione seguente e disegnarne approssimativamente il grafico
f ( x)
x 5
x 4x
2
Svolgimento
Dominio
Segno ed intersezione con gli assi
Limiti ed eventuali asintoti
Studio della derivata prima
Disegnare il grafico di f
5
Esercizio 10
La popolazione degli stambecchi del Parco Nazionale dello Stelvio è composta da circa 800
esemplari adulti (dati del 2004), la cui lunghezza L varia tra i 130 e i 160 centimetri. Più
precisamente la lunghezza L è distribuita come nella tabella che segue, dove F rappresenta la
frequenza assoluta di ogni classe:
L (cm)
F
[127,5 – 132,5) 32
[132,5 – 137,5) 41
[137,5 – 142,5) 158
[142,5 – 147,5) 268
[147,5 – 152,5) 116
[152,5 – 157,5) 70
[157,5 – 162,5) 115
a) Disegnare l’istogramma delle frequenze assolute di L.
b) Calcolare la lunghezza media e la deviazione standard degli individui della popolazione.
Svolgimento
a)
b)
Esercizio 11
Si consideri la funzione f definita sull’intervallo [3, 3] come nella figura sotto riportata. Disegnare il
grafico della sua derivata f ’.
Grafico di f
Grafico di f ’
6