Scuola di Dottorato in
“High Mechanics and Automotive Design &
Technology”
“Meccanica Avanzata e Tecnica del Veicolo”
QUADERNI
Quaderno n. 1:
Il metodo di Plemelj per
l’integrazione di integrali singolari
prof. Antonio Strozzi
Meccanismo greco di Anticitera,
Museo nazionale archeologico, Atene
All'alta fantasia qui mancò possa;
ma già volgeva il mio disio e 'l velle,
si come rota ch'igualmente è mossa,
l'amore che move il sole e l'altre stelle.
Dante, Paradiso
1
Introduzione
Il primo quaderno della Scuola di Dottorato in “High Mechanics and Automotive
Design & Technology”/“Meccanica Avanzata e Tecnica del Veicolo” riguarda il
metodo di Plemelj per l’integrazione di integrali singolari di Cauchy.
Questo quaderno è essenzialmente formato da appunti che ho raggruppato
durante l’approfondimento della tecnica di integrazione di Plemelj. Tali appunti sono
stati conservati nel loro aspetto embrionale, non possedendo di certo la dignità di
stampa. Con questa scelta si è voluto in qualche modo indicare il carattere principale
che questi quaderni devono possedere: quello di trasmettere stimoli culturali. A testi
limati e perfezionati, i quaderni preferiranno pagine probabilmente meno formali, ma
dai contenuti scientifici non meno stimolanti. Si ritiene infatti che al lavoro rifinito
nel contenuto e nel testo debba venire riservata la destinazione della pubblicazione su
rivista ad alta dignità scientifica.
La tecnica di integrazione di Plemelj mi ha permesso di ottenere risultati nel
campo dei problemi di contatto, quasi sempre descritti da equazioni integrali di
Cauchy. Gli articoli che ho prodotto nel campo degli integrali di Plemelj sono:
Monegato, G. & Strozzi, A. (2005) On the analytical solutions of two singular
integral equations with Hilbert kernel. J. Integral Equations, 17, 141-157.
Monegato, G. & Strozzi, A. (2008) The numerical evaluation of two integral
transforms, J. Comput. Appl. Math., 211, 173-180.
Prof. Antonio Strozzi
Coordinatore della scuola di Dottorato in
Meccanica Avanzata e Tecnica del Veicolo
2
LE FORMULE DI PLEMELJ
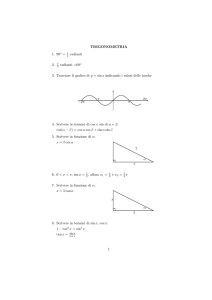
Si considera una funzione f(), dove f è una funzione complessa, e
una variabile reale. Per esempio, f() = 3 + i 2.
Si considera poi la funzione complessa di variabile complessa
F(z):
1 f
F z
d
2i
z
a
b
La funzione F(z) si chiama "analytic (or Cauchy)
representation of function f". La funzione F è una funzione analitica
"sectionally continuous", e cioè è analitica tranne che per una
discontinuità nell'attraversare la retta reale a - b.
Le proprietà della funzione F sono le seguenti:
1) La funzione F è analitica tranne che per il tratto a b;
2) La funzione F tende a 0 almeno come 1/z quando z diventa
infinito (si veda però il caso di f antisimmetrica o di f il cui integrale
sia nullo);
3) La funzione F ha un salto lungo il tratto a b, nel senso che F(z+)F(z-) è una funzione non nulla.
La funzione F tende a 0 quando z diventa infinito, Estrada p.
85. Infatti, se z diventa enorme, siccome l'intervallo di integrazione a
b è finito, il denominatore dell'integrando diventa enorme, e quindi
l'integrando diventa piccolissimo, giustificando così il fatto che
l'integrale si annulla per z infinito. La forza con la quale la funzione
F(z) tende a zero quando z diventa infinito è 1/z, come appare
dall'integrale di definizione di F(z) .
Si noti che nell'integrale la variabile di integrazione viene
indicata con e non con x, anche se essa è una variabile di
integrazione reale. Infatti usualmente z = x + i y, per cui, se adottassi
x come variabile di integrazione, l'integrale precedente diventerebbe:
f x
1
F z
dx
2i
a x x iy
b
e non è questo il significato che si intende dare all'integrale. Infine, il
termine 2 i viene introdotto per convenienza matematica.
Si considera un semplice esempio:
f
3
e quindi f viene assunta come funzione reale. Quindi F vale:
b
b
b
1
1 z
1
F z
d
d
z
d
2 i a z
2 i a z
a z
1
b z
b a z ln
a z
2 i
Siccome:
b z
lim z z ln
a b
a z
lim z
2
2
3
3
4
4
b z a b 1 a b 1 a b 1
a b z ln
....
a z
2
z
3 z2
4
z3
(per calcolare questo limite, si sostituisce 1/y a z , e si fa tendere y a
zero, calcolando col manipolatore algebrico lo sviluppo di Taylor
nell'intorno di y=0) allora F(z) dell'esempio precedente si annulla per
z come 1/z, come dovuto.
Si considerano nel seguito tre situazioni:
1 - caso z = x.
In questo caso F(x) vale:
1
1
b x
F x
b
a
x
ln
d
x a 2 i
2 i
a x
b
2 - caso z = x+.
F x
b x ei
b x
1
1
b
a
x
ln
i
b a x ln
i0
2i
x a e 2i
x a
dove si nota che il logaritmo e la funzione esponenziale si eliminano
mutuamente.
3 - caso z = x-.
F x
b x ei
b x
1
1
b
a
x
ln
i
b a x ln
i2
2i
x a e 2i
x a
Il salto della funzione analitica F "sectionally continuous" vale
quindi:
F x F x
1
x i i x f x
2i
La media dei due valori della funzione F sopra e sotto il salto
vale invece:
4
1
1
b x
F x F x
b
a
x
ln
F x
x a
2
2i
Le due formule precedenti costituiscono le formule di Plemelj
che, per una funzione generica f, sono:
1
1 f
F x F x F x
d
2
2 i
x
a
b
F x F x f x
La prima formula di Plemelj richiama lo sviluppo in serie di
Fourier di un salto, dove la funzione assume al centro del salto il
valor medio della funzione prima e dopo il gradino. Le proprietà
della somma e della differenza tra i valori di discontinuità della F
ricordano la lettura estensimetrica di una tensoflessione in una trave
effettuata applicando due estensimetri ai lati opposti di una sezione,
dove la somma dei due valori estensimetrici è collegata allo sforzo
normale e la differenza al momento flettente.
Una combinazione delle formule di Plemelj che mette in luce
la loro potenzialità nel calcolo di integrali di Cauchy è la seguente:
F x
F x
1 F F
d
i
x
b
a
Tale formula indica che, se si sa esprimere la funzione f da
integrare secondo Cauchy (cioè l'integrando è f()/(-x)) come salto
di una funzione analitica F "sectionally continuous", allora
l'integrale di Cauchy è strettamente collegato alla media della
funzione analitica prima e dopo il salto, e quindi l'integrale si calcola
immediatamente.
ESEMPI E CONTROESEMPI
Si riconsidera l'esempio precedente, e si verifica l'integrazione
con l'aiuto delle formule di Plemelj:
F x
F x
1
b x
b a x ln
;
x a
i
b x
d b a x ln
x a
a x
b
e questo risultato è corretto.
5
b
1 F F
1
d
d
i
x
i
x
a
a
b
La formula utile precedente va accompagnata con la formula:
1 F F
F z
d
2i
z
b
a
Si riconsidera la funzione analitica "sectionally continuous":
F z
1
b z
b a z ln
a z
2i
Se a questa funzione si somma un polinomio in z, il salto
F(x+)-F(x-) non cambia, dato che il polinomio è continuo
nell'attraversare il segmento che crea discontinuità ad F(z), mentre
cambia F(x+)+F(x-). Per esempio, se considero la funzione analitica
"sectionally continuous" F(z):
F z
1
b z
2
b
a
z
ln
A
Bz
Cz
a z
2i
allora il salto di F vale:
F x F x
1
x i i x
2i
mentre la semisomma dei due valori di discontinuità vale:
1
1
b x
2
F x F x
b
a
x
ln
A
Bx
Cx
x a
2
2i
In base alla formula:
F x F x
1 F F
d
i
x
b
a
dovrebbe valere il seguente integrale:
1
1
b x
2
b
a
x
ln
A
Bx
Cx
d
i
x a
i
a x
b
cioè:
b x
2
d b a x ln
A Bx Cx
xa
a x
b
6
il che è un risultato sbagliato. La ragione per la quale l'approccio
precedente produce risultati errati è che la funzione analitica
"sectionally continuous":
F z
1
b z
2
b a z ln
A Bz Cz
a z
2i
per z che tende all'infinito non si annulla come 1/z, ma invece tende
all'infinito come C z2. Quindi questa funzione F non rispetta la
condizione di comportamento tipo 1/z per z che tende ad infinito.
Similmente, se sommassi ad una funzione F il rapporto tra due
polinomi, questo presenterebbe dei poli dove il denominatore si
annulla, e quindi la funzione nel suo complesso non soddisfa in
genere la condizione che essa deve essere analitica tranne che lungo
il tratto a b. (Si veda però un esempio successivo, nel quale una
funzione analitica è formata da un rapporto di polinomi, più un'altra
parte che oscula i poli del polinomio.)
Si considera ora la funzione analitica "sectionally continuous":
F z
1 b z
ln
2i a z
Siccome:
lim z
2
2
3
3
4
4
b z a b a b 1 a b 1 a b 1
ln
....
a z
z
2
3 z3
4
z2
z4
questa funzione si comporta come richiesto per z infinito. Quindi:
i
1 b x e
1 b x
ln
ln
i
2 i x a ei 0 2 i x a
i
1 b x e
1
ln
i2
2i x a e 2i
F x
F x
b x
i
ln
x a
21i i i 1
1
2 F x F x 21i ln bx ax
F x F x
Quindi, impiegando la formula:
F x
F x
1 F F
d
i
x
b
a
si ottiene:
7
1 b x
1 1
ln
d
2i x a 2i a x
b
che è verificata.
Se invece considero la funzione analitica "sectionally
continuous":
F z
1
b z
z ln
a z
2i
questa funzione non si comporta come richiesto per z infinito, dato
che:
lim z
a 2 b2 1 a 3 b3 1 a 4 b4 1
b z
z ln
....
a b
a z
2
z
3 z2
4
z3
e quindi questa funzione non può essere impiegata per valutare un
integrale di Cauchy secondo la formula:
F x
F x
1 F F
d
i
x
b
a
SOMMA DI FUNZIONI ANALITICHE
Se però considero la funzione ottenuta sommando alla
funzione precedente il termine costante b-a:
F z
1 b z
z ln
b a
2i a z
questa si comporta come richiesto per z infinito, e quindi può venire
impiegata per il calcolo di integrali di Cauchy. In questo caso,
l'aggiunta di una parte di un polinomio (il termine costante b-a) è
quindi ammissibile.
Si considera un altro esempio nel quale si somma, ad una
funzione analitica con salto, un polinomio per far sì che la funzione
analitica si comporti come 1/z per z infinito. In questo caso la
formula del calcolo dell'integrale di Cauchy regge.
Si considera per esempio la funzione analitica F "sectionally
continuous":
F z z a
1
z b
dove 0 < Re < 1.
Per z infinito F(z) vale:
1
limz F z z 1 a b ......
z
8
Quindi occorre modificare la funzione F(z) aggiungendo un
polinomio in modo che essa si annulli come 1/z per z infinito:
F z z a
1
Si ha:
z b z 1 a b
b x ei x 1 a b
x a 1 b x ei x 1 a b
1
F x x a ei 1 2 b x ei x 1 a b
x a 1 b x ei 2 x 1 a b
x a 1 b x e i x 1 a b
F x x a
1 i 1 0
e
F x F x x a
b x 2i sin
1
F x F x x a b x 2 cos 2 x 21 a b
Quindi la relazione:
F x
F x
1
1 F F
d
i
x
b
a
diventa:
x a
2i sin a b
d
b x 2 cos 2 x 21 a b
i
x
a
b
1
1
cioè:
1 a b
1
d cot x a b x csc x 1 a b
a
x
b
1
Questa formula differisce per un coefficiente 2 dalla formula
(3.123) p. 96 di Estrada. Sbaglio io o Estrada?
Circa il tendere a zero di F come 1/z per z infinito, si nota che,
essendo:
1 f
F z
d
2i
a z
b
se f è pari in , siccome:
1 1
1
z
2
2 z z z 2
9
si ha:
1 f
z f
F z
d
d
2
2
2 i
2 i
a z
a z
b
b
e anche da questa espressione appare che F tende a zero come 1/z
per z infinito. Se invece f è dispari in , siccome:
1 1
1
2
2 z z z 2
si ha:
1 f
1 f
F z
d
2 z 2 d
2 i
z
2
i
a
a
b
b
e da questa espressione appare che F tende a zero come 1/z2 per z
infinito. Per esempio, se f()=1 (funzione pari), si ha:
z 1
1 1
z
1
1
F z
d
d
log
2
2
2 i a z
2 i
2 i
z 1
a z
b
b
dove questo F tende a zero come 1/z per z infinito. Se invece f()=
(funzione dispari), si ha:
b
1
1
F z
d
d
2
2
2 i a z
2 i
a z
b
z 1
1 2
1
d
2
zlog
2
2
2 i
2 i
z 1
a z
b
dove questo F tende a zero come 1/z2 per z infinito. Quindi, se f è
dispari, F non tende a zero come 1/z, ma come 1/z2 . Cosa vuol dire?
Considero ora una funzione espressa dal rapporto di due
polinomi:
F z
1
z
2i 1 z 2
Tale funzione si comporta come 1/z per z che tende ad infinito.
La funzione è inoltre continua nel passare il segmento a b, per cui:
F x F x 0
10
mentre il valor medio dei due valori estremali non si annulla:
1
1
z
F x F x
2
2 i 1 z 2
La formula:
F x F x
1 F F
d
i
x
b
a
in questo caso produce risultati errati. Infatti, se la funzione analitica
F è continua nel passare il segmento a b, allora il salto di F è nullo, e
quindi f()=0, dato che:
F x F x f x
Quindi una funzione analitica continua al passaggio del tratto
a b non rispetta la formula del calcolo dell'integrale di Cauchy. Il
risultato precedente può anche venire espresso nel modo seguente:
non esiste alcuna funzione f() tale che la sua rappresentazione
analitica secondo Cauchy sia una funzione continua nell'attraversare
il tratto a b. L'unico caso in cui questo accade è la funzione f() = 0,
che genera una funzione analitica nulla, la quale è continua
nell'attraversare il tratto a b.
Si noti inoltre che la funzione analitica F:
F z
1
z
2i 1 z 2
presenta due poli per z = i , e quindi la funzione F non è analitica
ovunque tranne lungo il tratto a b. In altre parole, il rapporto tra due
polinomi non soddisfa il requisito che deve possedere F per essere
una "analytic (or Cauchy) representation" di una funzione f.
Similmente un polinomio non soddisfa il requisito che deve
possedere F per essere una "analytic (or Cauchy) representation" di
una funzione f, dato che un polinomio non tende a 0 come 1/z per z
infinito. I poli del polinomio non possono capitare lungo il tratto a b,
dato che f è supposta Holderiana. I poli possono invece cadere ai due
estremi a oppure b., come accade quando studio una funzione del
tipo 1/1-x2.
Ritornando all'esempio precedente, posso rendere la funzione
precedente "sectionally continuous" moltiplicandola per una
opportuna funzione logaritmo e per z:
11
F z
z
z 1
z
log
z 1
1 z2
Per z infinito tale funzione tende a 0 come 1/z, che sembra un
risultato positivo (seguiranno critiche). Però tale funzione possiede
due poli indesiderati per z = i , che vanno eliminati. Siccome:
z 1
z log
z 1 z i
2
si costruisce la seguente funzione analitica depurata dei poli
indesiderati:
F z
z 1
z log z 1 2
z
1 z2
Si ha quindi:
1 x
x
log
i
x
i
0
x
x 1
2
x
1 x
x log
i x i 2 x
2
x 1
2
1 x
F x
F x
x
1 x2
x
1 x2
x
1 x2
F x F x
F x F x
1 x
2 x log x 1
i 2 x
ed infine, applicando la formula:
F x
F x
1 F F
d
i
x
b
a
si ottiene l'integrale di Cauchy:
x
1 x2
b
1
2 i 2
1 x
2
x
log
1 2 x d
1
x
i
a
cioè:
b
2
1
x
1 2 x d 1 x 2
a
1 x
x log 1 x 2
12
che rappresenta un risultato esatto. Tuttavia, la forma iniziale
F z
1
z
2i 1 z 2
della funzione analitica faceva pensare al calcolo del seguente
integrale:
b
1
d
2
a 1 x
mentre invece si è calcolato il seguente integrale:
b
2
1
1 2 x d
a
Le ragioni di questo cambio di rotta stanno nel fatto che si è
modificato il precedente rapporto di polinomi moltiplicandolo per z
e per un termine logaritmico, ipotizzando che la funzione analitica si
dovesse comportare come 1/z per z infinito. Siccome però
l'integrando:
1 2
è antisimmetrico, la corrispondente funzione analitica deve
comportarsi come 1/z2 per z infinito. Si prova nel seguito a calcolare
il seguente integrale:
b
1
d
2
a 1 x
cercando di costruire una funzione analitica che si comporti come
1/z2 per z infinito. Si parte da:
F z
z
1 z2
che però non va bene perché è continua nell'attraversare il segmento
-1 , 1. Si considera quindi la seguente funzione analitica:
F z
z
z 1
log
2
z 1
1 z
che si comporta giustamente come 1/z2 per z infinito. Però tale
funzione analitica possiede due poli indesiderati per z = i , che
vanno eliminati. Siccome:
1
1 1
1
1 z2 2 1 i z 1 i z
la funzione analitica può venire divisa nella somma di due parti:
13
1 1
1
z 1
z 1
F z
z log
z log
2 1 i z
z 1
z 1 z i 1 i z
1 1
1
z 1
z 1
z log
z log
z 1 2 1 i z
z 1 2
2 1 i z
1
1 z2
z 1
z 1
z log
z log
z 1
z 1
z 1
z log z 1 2
Si può verificare che nell'espressione precedente della
funzione analitica F i poli risultano osculati. Si ha quindi:
F z
1
1 z2
z 1
z
log
z 1 2
F x
1
1 x2
1 x
x log 1 x i i 0 2
1
1 x2
1 x
x
log
i
i
2
1 x
2
1
1 x
2
x
log
1 x
1 x 2
1
i 2 x
1 x2
F x
F x F x
F x F x
e quindi la formula:
F x F x
1 F F
d
i
x
b
a
diventa:
1
1 x2
1
x
1
2i
1 x
d
2
2 x log 1 x i
1 1 x x
x
1
1
d
2
1 x2
1 1 x x
1
1 x
x log 1 x 2
che è un risultato corretto.
Si considera ora un secondo esempio di funzione f(x) espressa
come rapporto tra due polinomi:
14
z i
f ( x)
1
1 x tan 2
2
e si considera la corrispondente funzione F(z) sectionally
continuous:
1
1
1
F ( z)
dx
2
2
1 1 x tan x z
Questo integrale viene calcolato come segue:
1
1
1 x 2 tan 2 ( x 2 tan 2 1
1
1
dx
dx
2
2
1 x 2 tan 2
x z
1 1 x tan x z
1
1
1
x2
1
2
dx
tan
xz
1 x 2 tan 2 x z dx
1
1
1
1 z tan 2 x 2 y 2 y 2 1 dx
log
1 x 2 tan 2 x z
1 z
1
1
1
1 z
xz
1
1
2
2
2
log
tan
dx
z
tan
dx
2
2
1 1 x 2 tan 2
1 z
1 1 x tan x z
1
1
1 z
1
1
1
2
2
2
log
z tan
dx
z
tan
dx
2
2
1 1 x 2 tan 2
1 z
1 1 x tan x z
1
1 z
1
1
2
2
log
2 z tan z tan
dx
2
2
1 z
1 1 x tan x z
1
Raggruppando gli integrali, ottengo:
1
1 z
1
1
1
F z
dx
log
2
z
tan
2
2
1 z 2 tan 2 1 z
1 1 x tan x z
Si nota che, nonostante la funzione analitica F(z) includa un
rapporto di polinomi, F(z) è continua per z = +/- i/tan . Non riesco
invece a dimostrare se è continua anche la derivata prima di F,
perché i calcoli sono troppo pesanti. Dovrebbe esserlo, perché F è
analitica.
Voglio verificare se vale la formula di integrazione:
F x F x
1 F F
d
i
x
b
a
Si ha:
15
1
log1 x i log1 x i 0 2 x tan
1 x tan 2
1
log1 x i log1 x i 2 2 x tan
1 x 2 tan 2
1
F x
2 log1 x 2 log1 x 4 x tan
2
1 x tan 2
1
F x
2 i
1 x 2 tan 2
F x
F x
F x
F x
2
e quindi la formula di integrazione è verificata.
Si considera un altro esempio:
F z
1
z2 1
z 1
1/ 2
z 1 1/2
Si nota che tale funzione si comporta come 1/z per z infinito,
come richiesto. Si ha inoltre:
F x 1 x
1/ 2 i / 2
F x 1 x
1/ 2 i / 2
e
F x F x
F x F x
e
1 x 1/2 e i 0/2
1 x 1/2 e i 2 /2
1
1 x2
1
1 x
2
e
i / 2
e
i / 2
La relazione:
F x F x
1
1 x2
1
ei / 2
ei / 2
1 x2
1
a
diventa:
16
e i 3 / 2
2i sin
1
1 x2
e i / 2
2i
2
1 x2
1 x2
1
2 cos 0
2
1 x2
1 F F
d
i
x
b
e i / 2
1
1
2i
1
1
0
d
d 0
2
i 1 1 2 x
1 1 x
confermando così un noto integrale.
Si considera ora il calcolo del seguente integrale di Cauchy:
1
1
1
d
2
2
2 1 tan x
1
1
1 x 1
Tale integrale si calcola nel modo seguente:
1
1
1
d
2
2
2 1 tan x
1 1
1
1
1
1
1
1
1
d
x
d
2
2
2
2
1 1 2 1 tan
1 1 2 1 tan x
1
1
1
1
cos x
d
2 1 2 tan 2 x
1 1
Inoltre:
17
1
1
1
1
d
2 1 2 tan 2 x
1 1
1
1
1
1
2
1
2
d tan
d
2
2
2 1 tan x
1
1 1 2 x
1
1
1
1
1
x
1
1
1
2
tan
d x
d
2
2
2
2
1 1 2 1 tan
1 1 2 1 tan x
2
1
1
1
1
2
tan x cos x
d
2
2
1 1 2 1 tan x
2
1
x tan 2 cos
1
1
1
d
2 1 2 tan 2 x
1 x 2 tan 2
1
1
In conclusione:
1
x 2 tan 2 cos
cos
1
1
d
cos
2
2
1 x 2 tan 2
1 x 2 tan 2
1 1 2 1 tan x
Si ritorna nel seguito al calcolo dell'integrale proposto tramite
le formule di Plemelj. A tale scopo, si considera la funzione
analitica:
F ( z)
1
z
2
2
z 2 1 1 z tan
Tale funzione è dispari in z, e quindi deve tendere come 1/z2
per z . Inoltre occorre rimuovere i poli per z =i/tan . Per
osculare i poli, scrivo:
F\ ( z)
1
z
z 1 1 i z tan
2
; F2 ( z)
1
z
z 1 1 i z tan
2
; F z
Sottraggo opportuni termini per osculare i poli:
18
1
F\ ( z) F2 ( z)
2
z
1
F\ ( z )
1 i z tan z 2 1
z
1
cos
z 2 1 z i 1 i z tan z 2 1
tan
z
1
F2 ( z )
1 i z tan z 2 1
z
1
cos
z 2 1 z i 1 i z tan z 2 1
tan
z
z
i z sin
1
2
2
2
z 2 1 1 z tan 1 z tan
z
F ( z)
2
Però la seconda frazione non tende a zero, come si
richiederebbe, come 1/z2, ma solo come 1/z. Pur con questo difetto,
provo a calcolare il precedente integrale con la funzione analitica:
i z sin
1
2
2
2
z 2 1 1 z tan 1 z tan
z
F ( z)
2
F(x )
F(x )
x
1 x2
x
1 x2
e
e
i
2 e i 0
i x sin
1
1 x 2 tan 2 1 x 2 tan 2
i
2 e i
i x sin
1
2
1 x tan 1 x 2 tan 2
2
i
i
2 i x sin
1
e 2 e 2
F(x ) F(x )
2
2
2
2
1 x tan 1 x tan
1 x2
x
2 i x sin
2 i x sin
1
2 cos
2
2
2
2
2 1 x tan 1 x tan 1 x 2 tan 2
1 x2
i
x i 2
1
e e 2
F(x ) F(x )
2
2
2
1
x
tan
1 x
x
2i x
1
1
2 i sin
2
2
2 1 x 2 tan 2
1 x2
1 x 2 1 x tan
x
e quindi la relazione:
F x F x
1 F F
d
i
x
b
a
diventa:
19
1
2 i x sin
2i
1
1
d
2
2
i
1 x 2 tan 2
1 1 2 1 tan x
1
i x sin
1
1
d
2
2
1 x 2 tan 2
1 1 2 1 tan x
dove il risultato precedente è errato, dato che l'integrale è reale e non
immaginario. Il risultato corretto infatti è:
1
cos
1
1
d
2
2
1 x 2 tan 2
1 1 2 1 tan x
Provo a calcolare il precedente integrale tramite una tecnica
diversa. Noto che una formula di Plemelj è:
F x
1
1 f
f x
d
2
2i
x
a
b
Se quindi f è funzione reale, la parte reale di F+ rappresenta la
funzione f , mentre la parte complessa rappresenta (a meno di 1/2)
l'integrale di Cauchy di f. (Oppure la parte reale di F+ rappresenta
l'integrale di Cauchy di f ,mentre la parte complessa rappresenta la
funzione f. Questo significa che, se f è reale, mi basta trovare
l'espressione corretta della funzione analitica per z+. Si riconsidera
quindi la funzione analitica F:
F ( z)
i z sin
1
2
2
2
2
z 2 1 1 z tan 1 z tan
z
nella quale, come già osservato, la seconda frazione non tende a
zero, come si richiederebbe, come 1/z2, ma solo come 1/z. Si pone al
numeratore della seconda frazione z = i/tan :
F ( z)
cos
1
2
2
2
z 2 1 1 z tan 1 z tan
z
2
e questa funzione analitica adesso tende a zero, come richiesto, come
1/z2, ma tale funzione analitica è corretta solo per z+. Applico quindi
la precedente formula di Plemelj:
20
0
i
2e 2
cos
1
2
1 x tan 1 x 2 tan 2
1 x2
cos
x
1
i
2
2
2
2
1 x 2 1 x tan 1 x tan
F(x )
x
e
i
2
e tale formula implica che:
1
cos
1
1
d
2
2
1 x 2 tan 2
1 1 2 1 tan x
che è un risultato corretto. Questo approccio è citato in Tricomi,
Integral Equations, p.168.
La tecnica precedente vale però solo se la funzione f è reale.
Riconsidero quindi ancora il calcolo dell'integrale:
1
1
1
d
2
2
1 1 2 1 tan x
1 x 1
cercando di sviluppare una tecnica di validità più generale. Scrivo:
z
1
F\ ( z )
1 i z tan z 2 1
z
1
cos
z 2 1 z i 1 i z tan z 2 1
tan
z
1
F2 ( z )
1 i z tan z 2 1
z
1
cos
z 2 1 z i 1 i z tan z 2 1
tan
F z
z
z
1
F\ ( z) F2 ( z)
2
Si nota che le due parti di F non sono antisimmetriche, e
quindi è giusto che tendano a 0 come 1/z. Considero la prima parte:
21
z
1
cos
2
1 i z tan z 1
F\ ( z )
0
i
i
i
1
x
1
x
2
2
2 cos
F\ ( x )
e
e
cos
e
1 i x tan
1 i x tan 1 x 2
1 x2
F\ ( x )
2
i
i
i
1
x
1
x
e 2 e 2 cos
e 2 cos
1 i x tan 1 x 2
1 i x tan 1 x 2
2 cos
1
x
2 cos 2 cos
2
1 i x tan 1 x
2
1 i x tan
sin
2i x
2i x
1
2
F\ ( x ) F\ ( x )
2 1 i x tan
2 1 i x tan
1 x
1 x
F\ ( x ) F\ ( x )
e quindi:
1
2 cos
1
1 2i
1
d
1 i x tan
i 1 1 2 1 i tan x
1
1
cos
1
d
1 i x tan
1 1 2 1 i tan x
Similmente:
F2 ( z )
z
1
cos
2
1 i z tan z 1
0
i
i
i
1
x
1
x
2
2
2 cos
F2 ( x )
e
e
cos
e
1 i x tan
1 i x tan 1 x 2
1 x2
2
i
i
i
1
x
1
x
2
2
F\ ( x )
e e
cos
e 2 cos
1 i x tan 1 x 2
1 i x tan 1 x 2
2 cos
1
x
2 cos 2 cos
2
1 i x tan 1 x
2
1 i x tan
sin
2
i
x
2i x
1
2
F\ ( x ) F\ ( x )
1 x 2 1 i x tan
1 x 2 1 i x tan
F\ ( x ) F\ ( x )
e quindi:
22
1
2 cos
1
1 2i
1
d
1 i x tan i 1 1 2 1 i tan x
1
1
cos
1
d
1 i x tan
1 1 2 1 i tan x
Infine:
1
1
1
d
2
2
1 1 2 1 tan x
1
1
1
1
1
1
1
1
d
d
2 1 i tan x
2 1 i tan x
2
2
1 1
1 1
cos
1 cos
1 cos
2 1 i x tan 2 1 i x tan 1 x 2 tan 2
che è un risultato corretto.
Si calcola ora l'integrale:
1
1
2
1
d
2
2
2 1 tan x
1 1
1
1
1
1
1
1
1
1
d
d
2
2
tan 2
1 1 2 x
1 1 2 1 tan x
x tan 2 cos
x cos
1
0
2
2
2
tan
1 x tan 1 x 2 tan 2
Si calcola ora l'integrale:
1
i
x 1 x
1
dx
1 1 x 2 1 x x y
23
Si considera la seguente funzione analitica:
z 1
z 2 1 z 1
z
F z
i
1
i
i x 1 x
e 1
1 x2 1 x
1 x
1
e
2 1 x
1 x
F x
F x
i
ix
i
F x
2 i x 1 x
sinh 2
2 1 x
1 x
F x
2 i x 1 x
cosh
1 x2 1 x
F x
F x
1
1
i
i
1
ix
1
dx
1 2 1 x
1 x2
i
1 x
tanh
1 x
cosh
Si calcola ora il seguente integrale, di interesse nella
determinazione della soluzione analitica di una equazione integrale
di Fredholm di seconda specie con nucleo di Hilbert:
1
i
1
1 1 x
x
dx
2
2 x y 1 x 1 x tan 2
1 1 x
dove è reale, -1<<1.
Si scrive:
1
1
i
1 1 x
x
dx
2 x y 1 x 1 x 2 tan 2
1 x
1
1
1
2
1
1
1
2
1
i
1 1 x
x
dx
1 x 2 x y 1 x 1 i x tan
1
1
1
1 x2 x
i
x
1 x
dx
y 1 x 1 i x tan
24
e si considerano i due integrali separatamente. La funzione analitica che si
considera per il primo integrale è:
i
i
1
1 z 1
z 1
F1 z
z
z
z 1
1 i z tan z 2 1 z 1
i
z
tan
i
1
1 z 1
i
z
e 2
1 i z tan z 2 1 z 1
tan
Quindi:
F1 z
F1 x
z 1 i
i
z
e 2
tan
z 2 1 z 1
i
1
i 1 x
i
x
e
e 2
1 i x tan 1 x 2 1 x
tan
1
1 i z tan
F1 x
1
i
1 i x tan 1 x 2
1 x i
i
e 2
e
x
tan
1 x
i
i x
2
1 i x tan 1 x 2
1 x
1 x
i
2
1 i x tan 1 x 2
1 x i
i
e 2
cosh
x
tan
1 x
F1 x F1 x
1
F1 x F1 x
1
1
i
1
i 1 i tan 1 2
1
i x
1
1 i x tan 1 x 2
sinh
1 i
1
i
e 2
d
cosh
tan
1
x
1 x
1 x
i
sinh
1
i
1
1
1
d
1 i tan 1 2 1 x
1
ix
1 i x tan 1 x 2
i
1
e 2
1
i
1
1
1 x
tanh
d
1 x
tan cosh 1 1 i tan 1 2 x
Si considera ora il secondo integrale. La funzione analitica che si
considera per il secondo integrale è:
25
i
i
1
1 z 1
z 1
F2 z
z
z
z 1
1 i z tan z 2 1 z 1
i
z
tan
i
1
1 z 1
i
z
e 2
1 i z tan z 2 1 z 1
tan
Quindi:
F2 z
F2 x
z 1 i
i
z
e 2
tan
z 2 1 z 1
i
1
i 1 x
i
x
e
e 2
1 i x tan 1 x 2 1 x
tan
1
1 i z tan
F2 x
1
i
1 i x tan 1 x 2
F x
F2 x
1
2
1 x i
i
e 2
e
x
tan
1 x
i x
2
1 i x tan 1 x 2
F2 x F2 x
i
2
1 i x tan 1 x 2
1
1
i
1
i 1 i tan 1 2
1
1 x
1 x
i
sinh
1 x i
i
e 2
cosh
x
tan
1 x
1 i
1
i
e 2
d
cosh
tan
1
x
i x 1 x
1
1 i x tan 1 x 2 1 x
i
sinh
1
i
1
1
1
d
1 i tan 1 2 1 x
1
ix
1 i x tan 1 x 2
i
1
e 2
1
i
1
1
1 x
tanh
d
2
1 x
tan cosh 1 1 i tan 1 x
Infine:
26
1
1
i
1 1
d
2
2
1 2 x 1 1 tan
1
i
i
x 1 x
tanh
1 x 2 tan 2 1 x 2 1 x
1
i
1
1
1
1
d
sinh 2
2 1 2 tan 2 x
tan cosh
1 1
1
1
1
i tan cosh 2
d
2 1 2 tan 2 x
1 1
Quindi:
1
1
i
1 1
d
2
2
1 2 x 1 1 tan
1
i
i
x 1 x
tanh
1 x 2 tan 2 1 x 2 1 x
x tan 2 cos
i
1
sinh 2 1 x 2 tan 2
tan cosh
i tan cosh 2
cos
1 x 2 tan 2
cioè:
27
1
1
i
1 1
d
2
2
1 2 x 1 1 tan
1
i
x
2
2
1 x tan 1 x 2
i
cosh 2 cos
x sin tanh 2
1 x
i
tanh
2
2
1 x
cosh 1 x tan
1 x 2 tan 2
Per = 0 tale integrale coincide col seguente integrale:
1
cos
1
1
d
2
2
1 x 2 tan 2
1 1 2 1 tan x
Per = 0 l'integrale precedentemente calcolato coincide col seguente
integrale:
1
1
i
1
ix
1
dx
1 2 1 x
1 x2
i
1 x
tanh
1 x
cosh
Si considera di nuovo il calcolo del precedente integrale:
1
i
1
1 1 x
x
dx
2
2
1 1 x 2 x y 1 x 1 x tan
dove questa procedura di calcolo che si rivelerà sbagliata. In linea coi
calcoli precedenti, si considerano separatamente le due parti dell'integrale:
i
i
z z 1
1
z z 1
F1 z
2
z 1
1 i z tan z 2 1 z 1
z
1
i
z
tan
z z 1 i
1
2
i cos e
2
1 i z tan z 1 z 1
Da calcoli numerici, non sembra che tale funzione calcolata
per z = i/tan si annulli, e quindi la parte aggiunta non effettua il
compito osculante. Procedendo comunque con i calcoli, si ha:
28
F1 x
0
i
x
i
i 1 x
2
2
1
2
2
e e
ei 0 e i i cos e 2
1 x
1 i x tan 1 x 2
i x
1
1 i x tan 1 x 2
F1 x
2
i
x
i
i
1
1 x i 2 2 i 2
2
2
e e
e
e
i cos e 2
1 x
1 i x tan 1 x 2
ix
1
1 i x tan 1 x 2
F x
F1 x
i
1 x
2
e i cos e
1 x
1
i
1 x
2
e i cos e
1 x
ix
1
1 i x tan 1 x 2
1 x
1 x
i
e
e 2 i cos e 2
i x 1 x i
2
sinh i cos e 2
1 i x tan 1 x 2 1 x
F x
F1 x
1
i x 1 x i
1
e e
1 i x tan 1 x 2 1 x
ix
2
1 i x tan 1 x 2
i
1 x
cosh
1 x
Quindi:
1
i
i
1
1
1
cosh
d
2 1
i
1
i
tan
x
1
1
i x 1 x i
1
sinh i cos e 2
1 i x tan 1 x 2 1 x
1
i
1
1
1
d
1 i tan 1 2 1 x
1
ix
1 i x tan 1 x 2
i
cos 2
1 x
tanh
i
e
1 x
cosh
Si considera ora il secondo integrale. La funzione analitica che si
considera per il secondo integrale è:
29
i
i
z z 1
1
z z 1
F2 z
2
z 1
1 i z tan z 2 1 z 1
z
1
i
z
tan
z z 1 i
1
2
i cos e
2
1 i z tan z 1 z 1
Quindi:
F2 x
0
i
x
i
i 1 x
2
2
1
2
2
e e
ei 0 e i i cos e 2
1 x
1 i x tan 1 x 2
i x 1 x i
1
e i cos e 2
1 i x tan 1 x 2 1 x
F2 x
2
i
x
i
i
1
1 x i 2 2 i 2
2
2
2
e
e
e
e
i
cos
e
1 x
1 i x tan 1 x 2
ix
1
1 i x tan 1 x 2
F x
F2 x
2
ix
1
1 i x tan 1 x 2
ix
2
1 i x tan 1 x 2
F2 x F2 x
i
1 x
2
e i cos e
1 x
i
e
e 2 i cos e 2
i
1 x
2
sinh 2 i cos e
1 x
ix
1
1 i x tan 1 x 2
ix
2
1 i x tan 1 x 2
1 x
1 x
i
1 x
cosh
1 x
Quindi:
30
1 x
1 x
i
e
e
1
i
i
1
1
1
cosh
d
2 1
i
1
i
tan
x
1
1
ix
1
1 i x tan 1 x 2
1
1
1 i tan 1 2
1
i
1 x
2
sinh i cos e
1 x
i
1
1
d
1 x
i x 1 x i
i cos 2
tanh
e
1 i x tan 1 x 2 1 x
cosh
Infine:
1
i
1
1 1
d
2 x 1 1 2 tan 2
1 1
i
x
2
2
1 x tan 1 x 2
i
cos x tan cosh 2 i sinh 2
1 x
tanh
1 x
cosh 1 x 2 tan 2
Il precedente integrale è sbagliato, dato che per =0 non
coincide con il seguente risultato:
1
x 2 tan 2 cos
cos
1
1
d
cos
2
2
1 x 2 tan 2
1 x 2 tan 2
1 1 2 1 tan x
Si considera nel seguito un altro integrale di interesse nella
determinazione della soluzione analitica di una equazione integrale
di Fredholm di seconda specie con nucleo di Hilbert:
1
1
1 1 x 2
x
1 x
dx
2
1 x 1 x tan 2
i
dove è reale, -1<<1.
Per il calcolo del precedente integrale, si considera il seguente
integrale di Cauchy, nel quale si porrà y = 0:
1
i
1
1 1 x
x2
dx
2 x y 1 x 1 x 2 tan 2
1 1 x
31
Si scrive:
1
1
1
1
1 x2 x
1
1
2
1
1
1
2
1
1
i
x
1 x
dx
y 1 x 1 x 2 tan 2
1
1 x2 x
2
i
x2
1 x
dx
y 1 x 1 i x tan
i
1 1 x
x2
dx
2 x y 1 x 1 i x tan
1 x
1
Per il calcolo del primo integrale, si considera la seguente funzione
analitica:
32
F z
1
1 i z tan
i
i
z 1
z
z 1
z z 1 z z 1
2
z 1
z 1 i
i
2
z
e
tan
z 2 1 z 1
1
1 i z tan
z
i
x
1 i x tan 1 x 2
i
x
1 i x tan 1 x 2
F x
F x
i
z
tan
1 x i
i
2
x
e
e
tan
1 x
1 x i
i
e 2
e
x
tan
1 x
F x
2i
x
1 i x tan 1 x 2
1 x i
sinh
x
1 x
F x
2i
x
1 i x tan 1 x 2
1 x i
i
e 2
cosh
x
tan
1 x
F x
F x
1
1
1 i tan 1 2
1
i
x
1 i x tan 1 x 2
1 i
1
i
e 2
d
cosh
1
tan
x
1 x i
sinh
x
1 x
1
i
1
2 1
1
d
1 i tan 1 2 1 x
1
i
i
x2 1 x
tanh
1 i x tan 1 x 2 1 x
1
i e 2
1
1
d
tan cosh 1 1 i tan 1 2 x
Per il calcolo del secondo integrale, si considera la seguente funzione
analitica:
33
1
1 i z tan
F z
i
i
z 1
z
z 1
z
z
z 1
z 2 1 z 1
i
z
tan
z 1 i
i
z
e 2
tan
z 2 1 z 1
1
1 i z tan
z
1 x i
i
x
i
x
e
e 2
1 i x tan 1 x 2 1 x
tan
i
x
1 i x tan 1 x 2
F x
F x
1 x i
i
e 2
e
x
tan
1 x
F x
2i
x
1 i x tan 1 x 2
1 x i
sinh
x
1 x
F x
2i
x
1 i x tan 1 x 2
1 x i
i
2
x
cosh
e
tan
1 x
F x
F x
1
1
1 i tan 1 2
1
i
x
1 i x tan 1 x 2
1
1 i
1
i
2
cosh
e
d
1
tan
x
1 x i
sinh
x
1 x
1
2
1 i tan 1 2
1
i
1
1
d
1 x
i
i
x2 1 x
tanh
1 i x tan 1 x 2 1 x
1
i e 2
1
1
d
2 x
tan cosh
1
i
tan
1
1
Infine:
34
1
1
i
1
2
1
d
2
2
2 1 1 tan x
1
1
i
x2
1 x 2 tan 2 1 x 2
1
i
tan cosh
1
i
1 x
tanh
1 x
sinh 2 i tan cosh 2 1
d
2
2
2
x
1
tan
1
Quindi:
1
i
1 1
2
1
d
2
2
2
1 1 1 1 tan x
i
i
x2 1 x
i
tanh
2
2
2
tan cosh
1 x tan 1 x 1 x
1
1
1
1
2
1
1
sinh 2
d
i
tan
cosh
2
d
2
2
2 1 2 tan 2 x
1
1 1 2 1 tan x
1
cioè:
1
i
1 1
2
1
d
2
2
2 1 1 tan x
1 1
i
i
x2 1 x
i
tanh
tan cosh
1 x 2 tan 2 1 x 2 1 x
cos
x cos
sinh
2
i
tan
cosh
2
1 x 2 tan 2
1 x 2 tan 2
Infine:
35
1
i
1 1
2
1
d
2
2
2 1 1 tan x
1 1
i
i
x2 1 x
tanh
1 x 2 tan 2 1 x 2 1 x
i cos sinh 2
x cos cosh 2
2
2
tan cosh 1 x tan
cosh 1 x 2 tan 2
Ponendo infine x = 0, si ottiene:
1
1
i
1
i cos sinh 2
d
2
2
tan cosh
1 2 1 1 tan
1
L'integrale giustamente si annulla per = 0, dato che l'integrando
diventa antisimmetrico. Per testare l'integrale precedente per = 0, occorre
calcolare l'integrale:
1
1
i
1
1
d
1 2 1 x
2
A tal fine si considera la seguente funzione analitica:
F z
z 1
z 2 1 z 1
z2
i
z 2i
i
i x 2 1 x
e x 2i
1 x2 1 x
1 x
x 2i
e
2 1 x
1 x
F x
F x
i
i x2
i
F x
2 i x 2 1 x
sinh 2 x 4 i
1 x2 1 x
F x
2 i x 2 1 x
cosh
1 x2 1 x
F x
F x
1
1
i
i
i
1
i x2 1 x
x 2i
1
d
tanh
cosh
1 2 1 x
1 x2 1 x
2
36
Ponendo infine x = 0, si ha:
1
1
i
1
2 i
d
cosh
1 2 1
Questo risultato coincide con l'integrale:
1
1
i
1
i cos sinh 2
d
2
2
tan cosh
1 2 1 1 tan
1
nel quale si ponga = 0, se si considera che:
lim 0
sinh 2
2
tan
Si riportano nel seguito altri calcoli, probabilmente sbagliati. Per il
calcolo del precedente integrale di Cauchy, si considera la seguente
funzione analitica F:
i
2
2
1
z
1
z
z
F z
2
2
2
2
i
1 z tan z 1
z 1 z
z 1
tan
i
2
i cos
1
z 1 z
1 z 2 tan 2 z 1 z 2 1 tan
Si ha:
37
i
2
i cos
1
1 x i x
e
2
2
2
tan
1 x tan 1 x
1 x
i
2
i cos
1
1 x i x
e
2
tan
1 x 2 tan 2 1 x
1 x
F x
F x
F x
F x
i
2
i cos
1
1 x i x
e e
e e
2
2
2
tan
1 x tan 1 x 1 x
i
2
i cos
2
1 x i x
sinh
cosh
2
2
tan
1 x tan 1 x 1 x 2
F x F x
i
2
i cos
1
1 x i x
e e
e e
2
2
tan
1 x tan 1 x 1 x 2
i
2
i cos
2
1 x i x
cosh
sinh
tan
1 x 2 tan 2 1 x 1 x 2
Quindi:
38
1
1
1
2
2
2
i 1 tan 1
1
i
i 2
1
i cos
cosh
sinh
d
2
tan
x
1
i
2
i cos
2
1 x i x
sinh
cosh
tan
1 x 2 tan 2 1 x 1 x 2
1
i
1
i
1
2
1
cosh
d
2
2
2 x
1 tan 1
i
1
1
i
2
i cos
1
1 x i x
sinh
cosh
2
2
tan
1 x tan 1 x 1 x 2
i
1
1
i cos
1
1
sinh
d
2
2
i tan
1
x
1
tan
1
1
i
1
1
2
1
d
2
2
2 x
1 tan 1
1
1
i
2
i
cos
1 x x
tanh
2
2
tan
1 x tan 1 x 1 x 2
i
1
1
cos
1
1
tanh
d
2
2
tan
1
x
1
tan
1
Si calcola ora l'integrale:
1
i
1
1
1
d
2
2
1 1 tan 1 x
1
1
i
i
1
1
1
1
1
1
1
d
d
2 1 1 i tan 1 x
1
i
tan
1
x
1
Si considera il primo integrale, che si tratta con la seguente funzione
analitica:
39
i
i
z 1
1
z 1
F z
z 1
1 i z tan z 1
z 1 i
1
2
e
1 i z tan z 1
i
z
tan
1 x i i 2 0 i 2
1 x i
1
1
2
2
e
e e
e e
1 i x tan 1 x
1 i x tan 1 x
1 x i i 2 2 i 2
1 x i
1
1
2
2
e
e
e
e e
1 i x tan 1 x
1 i x tan 1 x
F x
F x
F x
F x
1 x i
1
2e 2
e e
1 i x tan 1 x
1 x i
1
2
2 cosh 2e
1 i x tan 1 x
F x F x
1
1 x i
1
e e
1 i x tan 1 x
1 x i
1
2 sinh
1 i x tan 1 x
i
1
2
1
1
sinh
d
i
1
i
tan
1
x
1
1 x i
1
2
2 cosh 2e
1 i x tan 1 x
i
1 x i
1
i
1
1
2
d
cosh
e
sinh 1 i x tan 1 x
1 1 i tan 1 x
1
Si considera similmente il secondo integrale:
40
i
i
z 1
1
z 1
F z
z 1
1 i z tan z 1
z 1 i
1
2
e
1 i z tan z 1
i
z
tan
1 x i i 2 0 i 2
1 x i
1
1
2
2
e
e e
e e
1 i x tan 1 x
1 i x tan 1 x
1 x i i 2 2 i 2
1 x i
1
1
2
2
e
e
e
e e
1 i x tan 1 x
1 i x tan 1 x
F x
F x
F x
F x
1 x i
1
2e 2
e e
1 i x tan 1 x
1 x i
1
2
2 cosh 2e
1 i x tan 1 x
F x F x
1 x i
1
e e
1 i x tan 1 x
1 x i
1
2 sinh
1 i x tan 1 x
i
1
1
2
1
1
sinh
d
i
1
i
tan
1
x
1
1 x i
1
2
2 cosh 2e
1 i x tan 1 x
i
1 x i
1
i
1
1
2
d
cosh
e
sinh 1 i x tan 1 x
1 1 i tan 1 x
1
Infine:
i
1
1
1
1
d
2
2
1
x
1
tan
1
i
i
1 x
tanh
2
2
1 x tan 1 x
i
cosh 2 i x tan sinh 2
sinh 1 x 2 tan 2
1 x i
i
cosh 2 i x tan sinh 2
tanh
sinh
1 x 2 tan 2 1 x
Si è ora in grado di calcolare l'integrale di interesse:
41
1
i
1
1
2
1
d
2 x
1 2 tan 2 1
1
1
i
2
i
cos
1 x x
tanh
tan
1 x 2 tan 2 1 x 1 x 2
cos
i
tanh
tan
1 x 2 tan 2
1 x i
cosh 2 i x tan sinh 2
tanh
sinh
1 x
In particolare, per x = 0 l'integrale diventa:
1
i
1
1
d
2
2
2
1 tan 1
1
1
cosh 2
tanh sinh
i
cos
cos
i
tanh
tan
tan
i
cos
cosh 2
1
2
tan cosh
cosh
un risultato che sembra sbagliato.
Si affronta ora un terzo integrale di interesse nella
determinazione della soluzione analitica di una equazione integrale
di Fredholm di seconda specie con nucleo di Hilbert:
1
1 x
1 x
1
x
1 x
dx
1 x 1 x 2 tan 2
i
dove è reale, -1<<1.
Per il calcolo del precedente integrale, si studia il seguente integrale
di Cauchy, nel quale si porrà x = 0:
1
i
1 1
2
1
d
2
2
1
x
1
tan
1
1
1
i
i
1
1 1
1 1 1
2
1
2
1
d
d
2
1
1
i
tan
x
1
1
i
tan
x
1
1
1
1
42
Si considera il primo dei due integrali:
1
i
1 1
2
1
d
1
1
i
tan
x
1
1
per il quale si impiega la seguente funzione analitica:
i
z
z 1
F z
z
z 1 1 i z tan
i
z
z 1
z
z 1 1 i z tan
z 1
z
z 1
z 1
z 1 z
i 2 tan 1 ei
iz
tan
i
tan 2
tan
i 2 tan 1 ei
iz
z 1 i ei
z 1 tan tan
tan 2
i
i 2 tan 1 ei
ix
x
1 x i e i
1 x
F x
i
x
e
1 x
1 i x tan
1 x tan tan
tan 2
F x
i
i 2 tan 1 ei
ix
x
1 x i ei
1 x
e
i x
1 x
1 i x tan
1 x tan tan
tan 2
i
i e i
x
1 x
1 x
F x F x 2
i
x
sinh
cosh
1 x 1 i x tan
tan
1 x
i 2 tan 1 e
2i x
2
tan
tan 2
i
i
i e i
x
1 x
1 x
F x F x 2
i
x
cosh
sinh
1 x 1 i x tan
tan
1 x
Quindi:
1
i
1
1 x
1
ei
tanh
d
1
1
i
tan
tan
x
1
x
1
i
x
i ei
1 x
1 x
ix
tanh
1 x 1 i x tan
tan
1 x
i 2 tan 1 e
ix
tan cosh
tan 2 cosh
e cioè:
43
i
i
1
1 x 1
2
1
d
1
1
i
tan
x
1
x
1
i
i x2
i ei
1 x 1 x
tanh
tan
1 x 1 x 1 i x tan
i 2 tan 1 e
ix
tan cosh
tan 2 cosh
i
x
1 x
1 x 1 i x tan
i
i
1
ei tanh 1
1
d
tan 1 1 1 i tan x
Si considera il secondo dei due integrali:
1
i
1 1
2
1
d
1
1
i
tan
x
1
1
per il quale si impiega la seguente funzione analitica:
i
z
z 1
F z
z
z 1 1 i z tan
i
z
z 1
z
z 1 1 i z tan
z 1
z
z 1
z 1
z 1 z
i 2 tan 1 ei
iz
tan
i
tan 2
tan
i 2 tan 1 e i
iz
z 1 i e i
z 1 tan tan
tan 2
i
i 2 tan 1 e i
ix
x
1 x i e i
1 x
F x
i
x
e
1 x
1 i x tan
1 x tan tan
tan 2
F x
i
i 2 tan 1 e i
ix
x
1 x i e i
1 x
e
i x
1 x
1 i x tan
1 x tan tan
tan 2
i
i e i
x
1 x
1 x
F x F x 2
i
x
sinh
cosh
1 x 1 i x tan
tan
1 x
i 2 tan 1 e i
2i x
2
tan
tan 2
F x
F x
i
i e i
x
1 x
1 x
2
ix
cosh
sinh
1 x 1 i x tan
tan
1 x
Quindi:
44
i
1
1
1 x
1
e i
tanh
d
1
1
i
tan
tan
x
1
x
1
i
x
i e i
1 x
1 x
ix
tanh
1 x 1 i x tan
tan
1 x
i 2 tan 1 e
ix
tan cosh
tan 2 cosh
i
e cioè:
i
1
1 x 1
2
1
d
1
1
i
tan
x
1
x
1
i
i x2
i e i
1 x 1 x
tanh
tan
1 x 1 x 1 i x tan
i 2 tan 1 e
ix
tan cosh
tan 2 cosh
1
i
x
1 x
1 x 1 i x tan
i
i
e i tanh 1
1
d
tan
1
1
i
tan
x
1
Quindi l'integrale da calcolare vale:
1
i
i
1 1
i x2
2
1
1 x 1 x
d
tanh
2
2
2
2
1
x
1
x
1
x
1
tan
1
x
tan
1
1
i
i x 1 x sinh i i x tan cosh i
tan 2
tan 1 x
1 x 2 tan 2
1
i
tanh 1 sinh i i tan cosh i 1
d
tan 1 1
x
1 2 tan 2
cioè:
45
1
i
i
1 1
i x2
2
1
1 x 1 x
d
tanh
2
2
2
2
1
x
1
x
1
x
1
tan
1
x
tan
1
1
i
i x 1 x i sin i x tan cos
2
2
2
tan 1 x
1 x tan
tan
1
i
1
1
i tanh cos
d
2
2
1 1 1 tan x
1
i
1
2
1
i tanh cos
d
2
2
1 1 1 tan x
46
VECCHIO
Si scrive questo integrale come somma di due integrali:
1
i
1 1
2
1
d
2
2
1
x
1
tan
1
1
1
1
i
i
1 1 1
1
1 1 1
1
1
d
d
2
2
2
2
tan 1 1 1 x
tan 1 1 1 1 tan x
Si considera nel seguito l'integrale:
1
i
1 1
1
d
1 1 1 x
Si considera la seguente funzione analitica:
F z
z 1 z 1
z 1 z 1
i
1
i
i
i
i
i
i
1 x 2 2 0 1 x i 2 0 i 2
1 x 1 x
e e
1 i
e e
e 1
1 x
1 x
1 x 1 x
1 x 2 2 2 1 x i 2 2 i 2
1 x 1 x
e e
e
1 i
e
e 1
1 x
1 x
1 x 1 x
F x
F x
i
i
i
F x
1 x 1 x
2i
sinh 2
1 x 1 x
F x
1 x 1 x
2i
cosh
1 x 1 x
F x
F x
1
i
cosh
i
1
1
1
i
i
i
1 1
1
1 x 1 x
d i
sinh 1
1 x 1 x
1 1 x
i
i
1 1
1
1 x 1 x
d i
tanh
cosh
1 x 1 x
1 1 x
Quindi:
47
1
i
1 1
2
1
d
2
2
1
x
1
tan
1
1
tanh 1 x 1 x
i
tan 2 1 x 1 x
1
i
1
tan cosh
2
i
1 1 1
1
1
d
tan 2 1 1 1 1 2 tan 2 x
Si considera nel seguito l'integrale:
1
i
1 1
1
1
d
2
2
1 1 1 1 tan x
1
i
i
1
1 1
1 1 1
1
1
1
1
d
d
2
1
1
i
tan
x
1
1
i
tan
x
1
1
1
1
Si considera il primo dei precedenti integrali:
1
i
1 1
1
1
d
1
1
i
tan
x
1
1
per il quale si considera la seguente funzione analitica:
48
i
z 1 z 1
1
F z
1 i z tan z 1 z 1
z 1 z 1
z 1 z 1
i
i
z
tan
z 1 z 1 i
1
2 i
e
1 i z tan z 1 z 1
F x
1 x i i 0 1 x i i 2 0 i 2
1
e2 e 2
e 2 i
e e
1 x
1 i x tan 1 x
1 x 1 x i
1
2 i
e e
i
1 i x tan 1 x 1 x
F x
1 x i i 2 1 x i i 2 2 i 2
1
e2 e 2
e
e 2 i
e
1 x
1 i x tan 1 x
i
1
1 x 1 x
2 i
i
e
e
1 i x tan
1 x 1 x
F x
F x
1 x 1 x i
1
2 e 2 i
e e
i
1 i x tan 1 x 1 x
1 x 1 x i
2
2 i
sinh e
i
1 i x tan 1 x 1 x
F x
F x
1 x 1 x i
1
e e
i
1 i x tan 1 x 1 x
1 x 1 x i
2
cosh
i
1 i x tan 1 x 1 x
i
1
i
1
1 x 1 x
cosh
i 1 1 i x tan 1 x 1 x
1 x 1 x i
1
2 i
sinh e
i
1 i x tan 1 x 1 x
1
i
1
1 x 1 x
1 i x tan 1 x 1 x cosh
1
1 x 1 x i
2 i
sinh e
i
1 i x tan 1 x 1 x
49
Si considera il secondo dei precedenti integrali:
1
i
1 1
1
1
d
1
1
i
tan
x
1
1
per il quale si considera la seguente funzione analitica:
50
i
i
z 1 z 1
1
z 1 z 1
F z
1 i z tan z 1 z 1
z 1 z 1
i
z
tan
z 1 z 1 i
1
2 i
e
1 i z tan z 1 z 1
F x
1 x i i 0 1 x i i 2 0 i 2
1
e2 e 2
e 2 i
e e
1 x
1 i x tan 1 x
1 x 1 x i
1
2 i
e e
i
1 i x tan 1 x 1 x
F x
1 x i i 2 1 x i i 2 2 i 2
1
e2 e 2
e
e 2 i
e
1 x
1 i x tan 1 x
i
1
1 x 1 x
2 i
i
e
e
1 i x tan
1 x 1 x
F x
F x
1 x 1 x i
1
2 e 2 i
e e
i
1 i x tan 1 x 1 x
1 x 1 x i
2
2 i
sinh e
i
1 i x tan 1 x 1 x
F x
F x
1 x 1 x i
1
e e
i
1 i x tan 1 x 1 x
1 x 1 x i
2
cosh
i
1 i x tan 1 x 1 x
i
1
i
1
1 x 1 x
cosh
i 1 1 i x tan 1 x 1 x
1 x 1 x i
1
2 i
sinh e
i
1 i x tan 1 x 1 x
1
i
1
1 x 1 x
1 i x tan 1 x 1 x cosh
1
1 x 1 x i
2 i
sinh e
i
1 i x tan 1 x 1 x
51
In conclusione:
1
i
1 1
1
1
d
2
2
1
x
1
tan
1
1
i
i
1 x 1 x
i cosh 2 i x tan sinh 2
sinh e
2
2
1 x tan 1 x 1 x
1 x 2 tan 2
L'integrale cercato vale:
1
i
1 1
2
1
d
2
2
1
x
1
tan
1
1
tanh 1 x 1 x
i
tan 2 1 x 1 x
i
1
tan cosh
2
i
i
1
1 x 1 x
i cosh 2 i x tan sinh 2
sinh
e
tan 2 1 x 2 tan 2 1 x 1 x
1 x 2 tan 2
Per x = 0 l'integrale diventa:
1
i
1 1
d
2
2
1
1
tan
1
1
tanh
1
1
i
i sinh ei cosh 2
2
2
2
tan
tan cosh tan
che sembra un risultato sospetto per =0.
52
Si considera ora un altro esempio tratto dai polinomi di
Chebyshev. In generale si ha:
Tn
d U n x
2
1 1 x
1
Si considera per esempio n = 3. Si ha:
1
4 x 3 3x
d 4 x 2 1
2
1 1 x
Si vuole ritrovare l'integrale precedente tramite le formule di
Plemelj. Se scelgo come funzione F(z):
1
F z
z2
4z
1
3
3z
tale funzione si comporta per z infinito come:
4z 2 1
1
8 z4
Considero quindi:
1
F z
z
2
4z
1
3
3z 4 z 2 1
che si annulla correttamente per z infinito, come 1/z4. Si ha:
F x
F x
1
1 x
2
1
1 x
2
e
e
i
i
2
2
4z
4z
3
3
3z 4 z 2 1
3z 4 z 2 1
F x
i
i
1
2
e e 2 4 z 3 3z
1 x2
1 x2
F x
i
i
2
e e 2 4 z 3 3z 8z 2 2
2
1 x
F x
F x
1
1
2 cos 4 z 3 3z 8z 2 2 8z 2 2
2
1 x2
1
Quindi la relazione:
F x F x
1 F F
d
i
x
b
a
53
3
2 i sin 4 z 3z
2
diventa:
8 z 2 2
b
b
4 3 3
2
d
2
i
a 1 x
2 i sin
4 3 3
d 4 x 2 1
2
a 1 x
confermando così un noto integrale.
54
PRODOTTI DI FUNZIONI ANALITICHE
Fino ad ora si sono considerati esempi nei quali si
aggiungevano, ad una funzione F iniziale, delle parti in modo da far
tendere F ad infinito come 1/z quando z tende ad infinito, e di
aggiungere dei salti di funzione a funzioni che altrimenti
attraverserebbero il segmento -1 , 1 con continuità, cioè senza il
desiderato salto. Nel seguito si considerano esempi nei quali due
funzioni analitiche vengono moltiplicate tra loro.
Si osserva innanzitutto che, da un punto di vista pratico,
l'approccio precedentemente sviluppato può sembrare scarsamente
utile. Infatti si è in pratica detto che, per calcolare integrali di
Cauchy del tipo:
f
z d
a
b
si deve calcolare la rappresentazione analitica F della funzione f:
1 f
F z
d
2i
a z
b
Una volta calcolata la funzione F ed i suoi salti
nell'attraversare il segmento a b, l'integrale secondo Cauchy della f
vale:
1 f
d F x F x
i a x
b
Si può infatti obiettare che, se si è calcolata la funzione F, vuol
dire che si è già calcolato l'integrale secondo Cauchy per x = z, cioè
per un caso più generale rispetto ad una variabile reale x.
L'utilità pratica delle formule di Plemelj appare appieno
quando si considerano prodotti di funzioni analitiche. Si considera la
funzione Q:
Qn,m, z z a
n
z b m
dove n ed m sono numeri interi (positivi o negativi: i valori 0 e -1
sono leciti) e 0 < Re < 1. Inoltre si considera la funzione F
"sectionally continuous":
55
1 f
F z
d
2i
z
a
b
Per z infinito si ha:
limz Qn,m, z z nm ; limz F z
1
z
Considero nel seguito la funzione analitica ottenuta come
prodotto:
Q z F z
Tale funzione si comporta correttamente come 1/z per z
infinito se n+m=0, una condizione che si ritiene soddisfatta nel
seguito. Siccome:
Qn,m, x x a
n i n 0
e
b x m e i m
x a n b x m ei m 1 m x a n b x m ei
n
m
Qn,m, x x a ei n 2 b x ei m
x a n b x m ei m2n 1 m x a n b x m e i
il salto di Q F lungo il tratto a b vale:
Qn,m, x F x Qn,m, x F x
1 m x a n b x m ei F x 1 m x a n b x m e i F x
b
1 f
m
n
m i 1
d
1 x a b x e f x
2 t a x
2
1 x a
n
1 x a
n
m
m
b x
b x
m
e
i
b
1
1 f
f x
d
2
2 t
a x
b
sin f
d
cos f x
a x
m
mentre la somma dei valori di Q F prima e dopo il salto vale:
56
Qn,m, x F x Qn,m, x F x
1 m x a n b x m ei F x 1 m x a n b x m e i F x
b
1 f
m
n
m i 1
d
1 x a b x e f x
2 t a x
2
1 x a
n
b x
m
1 x a
n
b x
m
m
m
e
i
b
1
1 f
f x
x d
2
2
t
a
b
cos f
i sin f x
x d
i
a
Quindi la formula:
F x F x
1 F F
d
i
x
b
a
in questo caso si legge:
Q x
F x
Q x
F x
1 Q x F Q x F
d
i
x
b
a
e quindi tale formula produce il seguente integrale:
1 x a
m
n
b x
a
1
i
a
b
m
n
m
b
cos f
i sin f x
x d
i
a
b
b
sin f
d
cos f
a
m
x
oppure:
57
d
x a
n
b x
m
a
cos
a
n
a
sin
a
n
b
b
oppure:
x a
b x
n
a
a
b
n
b
f
cos
d
sin
f
x
x
a
b m f d
x
b
f
d
a
m
b
x
d
f
n
m
d
x
a
b
x
tan f x
x
a
m
b
b m f d
x
a
tan
a
b
n
b
f
d
a
m
b
x
d
oppure:
a
a
b
n
f
d
a
b m
b
x
d
tan
b
n
m
b
a b
f
n
m f
n
m
d x a b x tan f x
d
x a b x
x
a x
a
Si vuole verificare la formula precedente nel caso a=-1, b=1 e:
f x
1
1 x2
Siccome:
58
1
1
dx 0
1 x y 1 x 2
si ha, ricordando la condizione n+m=0:
1 n 1 m
1
n
m
d x 1 1 x tan
1 2 x
1 x2
1
1
Per esempio, per n=m=0 si ha:
1
1
1
1
1 x
d tan
1 1 2 x
x 1 1 x 2
1
Controllo l'integrale precedente considerando la funzione
analitica:
F z z 1
1
2
z 1
1
2
Si ha:
1 x
F x
1 x
1
2
e
i 1 x
1
2
1
2
1
i
2
1 x
F x
e
1
i
2
1 x
1
1 i 0
2
2e
1
1
1
1 x 2 i 1 x 2 ei 1 x 2
1
2
e
1
i
2
ei 1 x
1 x
1
i 2
2e
e quindi:
59
1
1 i 2
2
2e
i 1 x
1
2
1
1 x 2 e i
1
1
F x F x i 1 x 2 1 x 2 ei e i
2 i cos 1 x
1
2
1 x
1
2
1 x
2 i cos
1 x
1
1 x2
1
1
F x F x i 1 x 2 1 x 2 ei e i
2 sin 1 x
1
2
1 x
1
2
Quindi la formula:
F x F x
1 x
2 sin
1 x
1
1 x2
1 F F
d
i
x
b
a
diventa:
1 x
2 sin
1 x
b
1
1
2 i cos
1
1 x 2 i
a
1
1
1 2 x
d
cioè:
b
1
1
1
1 x
d tan
1 1 2 x
1 x 1 x2
a
confermando così l'esattezza dell'ultimo integrale.
Si considera ora l'integrale:
1
1
1 1 x 2
x
1 x
dx I1 ,
2
1 x 1 x tan 2
i
(17)
e lo si vuole calcolare tramite le formule di Plemelj, impiegando una
funzione analitica prodotto di due parti. La prima parte è:
Q z z 1
i
z 1 i
mentre la seconda parte si calcola come:
1 f
F z
d
2 i
1 z
1
e cioè:
60
1
1
1
F z
d
2
2
2
2 i
1
tan
1 1 z
Se i calcoli sono giusti, F deve comportarsi come 1/z per z infinito.
Si ha:
1
1
d
2
2
1 1 2 z 1 tan
1
1
1
1
1
d z
d
2
2
2
2
2
1 1 2 z 1 tan
1 1 1 tan
1
1
1
cos z
d
2
2
1 1 2 z 1 tan
Nel seguito si considera l'integrale:
1
1
1
d
2
2
1 1 2 z 1 tan
Si nota che la parte dell'integrando che moltiplica 1/(-z) è pari in ,
e quindi, introducendo un passaggio che facilita i successivi cambi di
variabile:
1 1
1
z
2
2 z z z 2
Quindi l'integrale precedente diventa:
1
1
1
1
1
1
d
z
d
2
2
2
2
2
2
2
1 1 2 z 1 tan
1 1 z 1 tan
Si considera nel seguito l'integrale
b
1
1
d
2
2
2 1 2 tan 2
a 1 z
Si effettua il cambio di variabili:
61
tan
tan
cos 2
; z
tan
tan
; d
d
cos tan
(5)
2
1
1 tan 2
2
e l'integrale precedente diventa:
1
1
1
1
d tan 2
d
2
2
2
2
2 1 tan
2
2
2
2
1
z
tan
tan
tan
tan
1
Impiegando l'identità trigonometrica:
1
cos2 cos2
tan2 tan2 sin2 sin2
(24)
si ottiene:
1
1
1
d
2
2
2
2 1 tan 2
1
z
1
cos 3
2
2
tan cos cos
d
2
2
2
2
sin
sin
sin
sin
Si effettua ora il cambio di variabili:
sin
sin
;
sin
sin
; d
ottenendo:
62
cos
d
sin
(26)
1
1
1
d
2
2
2
2 1 tan 2
1
z
1
tan 2 cos cos 2
sin 2
1
1
cos 2
cos
1
1
cos 2
d
1
1 2 sin 2
1 z 2 sin 2
d
d
2
2
2
cos
2 2
1
1
1 2 sin 2
1 2
1 2 2 2
Si considerano ora gli integrali calcolati per >1 (?):
1
1
d
2
2
2
2 1
1 1
1
2
d
1
2
1 2 2 2
1
1
Quindi:
1
1
1
d
2
2
2
2
2
1 1 z 1 tan
1 z 2 sin 2
1
sin 2
1
cos 1 2
1 2
1 2
1 z 2 sin 2
1
1
2
sin
1
cos 1 2
1 2
1 2
1 z 2 sin 2 cos 2
sin 2
1
cos 1 2
che non converge come 1/z**2 per z infinito, e quindi è sbagliato.
Inoltre:
63
1
1
1
1
1
1
d
z
d
2
2
2
2
2
2
2
1 1 2 z 1 tan
1 1 z 1 tan
1 z 2 sin 2 cos 2
sin 2
cos 1 z 2
1 z z
2
Impiegando tutti i risultati precedenti, la funzione analitica F
diventa:
1 z 2 sin 2 2
F z
sin
2 i cos
z 2 1 z cos 2
64
z2 1
1
1
1
1 1 x 2
1
1 x
1 x
1
x
1 x
dx I1 ,
2
1 x 1 x tan 2
i
x
1 x
dx I 2 ,
2
1 x 1 x tan 2
(17)
i
1
i
1
1 1 x
x
dx I 4 , , y
2 x y 1 x 1 x 2 tan 2
1 1 x
65
(17)
FORMULE UTILI
z 1
log
z 1
i
z i
z 1
log
z 1
2
i
z i
z 1
z log
z 1
2
z i
2
2 2 1
z 1
limz log
....
z 1
z 3 z3
z 1
log
z 1
z 1
log
z 1
z i z i
i z i i
2
2
3
2
z i
3
z i z i
i z i i
2
2
3
2
z i
z 1
z log
z 1
z 1
z log
z 1
z i
i 1 z i
2
2
2
z i
z i
2
z i
z i
2
2
i 1
2
; log i i
2
2
i
i
z 1
z 1
2
e
;
z 1
z 1
i
3
2
logi i
z
tan
1
z 1
2
sin ;
i
z
tan
z
z 1
i
z
tan
F z
1
z 1
F z
z 1
z2 1
i
z 2 1 z
z 1
2
; F x
i
tan
cos 2
sin
i
tan
z
i cos
i
z
tan
i
; F x
z
z2
i cos ;
2
e 2
1 x2
i
1 x
e
1 x
66
; F x
; F x
i
1 x2
i
1 x
e
1 x
67
PATTUME
quando si nota che, se si moltiplica una funzione F "sectionally
continuous" per una funzione analitica G continua nell'attraversare il
tratto a b, (per esempio un polinomio od un rapporto di polinomi che
non presenti singolarità nel tratto a b; inoltre F G deve annullarsi
per z ), allora il salto di F G vale:
G x f x G x
F x G x F x G x F x F x
La media della funzione nel salto vale invece:
G x
F x G x F x G x F x F x
Il legame tra la media del salto ed il salto diventa:
F x
F x
b
Siccome:
F x
F x
b
1 F F G
1 f G
G x
d
d
i
x
i
x
a
a
1 f
F x
d
i a x
b
la formula precedente può venire riscritta come:
f G
f
d
G
x
x
x d
a
a
b
b
Se quindi devo calcolare l'integrale di Cauchy di una funzione
interpretabile come prodotto di due parti, una prima parte f della
quale so individuare la rappresentazione analitica F, ed una seconda
parte il cui corrispettivo analitico (cambiando cioè con z) è
continuo nell'attraversare il tratto a b, cioè non presenta salti,
l'integrale secondo Cauchy del prodotto di tali funzioni si ottiene
calcolando l'integrale secondo Cauchy della sola funzione f, e
moltiplicando il risultato per la funzione G. La formula precedente
mostra che la funzione G viene estratta dall'integrale, una operazione
non certo lecita nella integrazione tradizionale.
Per esempio, si è visto che, se:
f
allora:
68
F z
1
a z
b
a
z
ln
b z
2i
F x
a x
1
i
b a x ln
2i
x b
a x
1
b
a
x
ln
i
2i
x b
F x F x x
F x
Se voglio quindi calcolare il seguente integrale secondo
Cauchy:
d
2
a x 1
b
dove:
G
1 2
scrivo:
F z G z
1
a z z
b
a
z
ln
b z 1 z 2
2i
che tende a 0 per z che tende ad infinito.
Inoltre:
1
a x
x
b a x ln
i
2
2 i
b x
1 x
1
a z
x
b a x ln
i
2
2 i
b z
1 x
F x G x
F x G x
x
1 x2
1
a x x
b a x ln
2
i
b x 1 x
F x G x F x G x x
F x G x F x G x
Quindi:
69
f G
f
x d G x x d
a
a
b
b
b
x
x
d
d
x
1 2
1 x 2 a x
1 x2
a
b
a x
b
a
x
ln
x b
In conclusione:
b
2
x
d
2
1 x2
a x 1
b
a x
b a x ln x b
a x x
d 2b a x ln
2
x
b
x
1 x
2
a 1 2
i
1
z
z 1 z
F1 z
2
2
1 i z tan z 1
i
z 1 z
z 1
tan
i
1
z 1 z
cos
2
1 i z tan z 1 z 1
Quindi:
70
F1 x
0
i
i
i
1
1 x i 2 0 i 2 x
2
2
e e cos
e e
1 i x tan 1 x
1 x 2
i
1
1 x i x
cos
e
2
1 i x tan 1 x
1 x
F1 x
2
i
i
i
1
1 x i 2 2 i 2 x
2
e
e e 2 cos
e
1 i x tan 1 x
1 x 2
i
1
1 x i x
cos
e
2
1 i x tan 1 x
1 x
F x
F1 x
1
i
ix
1
1 x
e e cos e e
2
1 i x tan 1 x 1 x
i
2
1 x i x
sinh cos cosh
1 i x tan 1 x 1 x 2
F x
F1 x
1
i x 1 x i
1
e e cos e e
1 i x tan 1 x 2 1 x
i
2
1 x i x
cosh cos sinh
1 i x tan 1 x 1 x 2
Quindi:
1
i
i
1
1
1
cosh
d
2 1
i
1
i
tan
x
1
1
ix
1
1 i x tan 1 x 2
i
1 x
sinh cos cosh
1 x
1
i
1
1
1
d
1 i tan 1 2 1 x
1
ix
1 i x tan 1 x 2
i
1 x
tanh cos
1 x
Si considera ora il secondo integrale. La funzione analitica che si
considera per il secondo integrale è:
71
1
z
z 1 z
F2 z
2
2
1 i z tan z 1
i
z
1
z
1
z
tan
i
i
1
z 1 z
cos
2
1 i z tan z 1 z 1
Quindi:
F2 x
0
i
i
i
1
1 x i 2 0 i 2 x
2
2
e e cos
e e
1 i x tan 1 x
1 x 2
i
1
1 x i x
cos
e
2
1 i x tan 1 x
1 x
F2 x
2
i
i
i
1
1 x i 2 2 i 2 x
2
e
e e 2 cos
e
1 i x tan 1 x
1 x 2
i
1
1 x i x
cos
e
2
1 i x tan 1 x
1 x
F2 x F2 x
i
ix
1
1 x
e e cos e e
1 i x tan 1 x 1 x 2
i
i x 1 x
2
sinh cos cosh
1 i x tan 1 x 2 1 x
F2 x F2 x
i
1
1 x i x
e e
1 i x tan 1 x 1 x 2
i
2
1 x i x
cosh
1 i x tan 1 x 1 x 2
Quindi:
72
1
i
i
1
1
1
cosh
d
2 1
i
1
i
tan
x
1
1
i
ix
1
1 x
sinh cos cosh
1 i x tan 1 x 1 x 2
1
i
1
1
1
d
1 i tan 1 2 1 x
1
ix
1 i x tan 1 x 2
i
1 x
tanh cos
1 x
Infine:
1
i
1
1 1
d
2
2 x 1 1 tan 2
1
1
i
i
i sin x
x 1 x
tanh
1 x 2 tan 2 1 x 2 1 x
1 x 2 tan 2
1 1 x i
ix
tanh
sin
1 x 2 tan 2 1 x 2 1 x
Inoltre:
73
1
i
1
1
2
1
d
2
2
2 x
1 tan 1
1
1
1
i
1 1
1
1
d
2
2 x
1
tan
1
1
1
i
1
1
1
1
1
d
2
2
2 x
1
tan 2
1
tan
1
1
Si calcola ora il seguente integrale:
1
1 i
1
1
d
2 x
1
1
1
A tal scopo si considera la seguente funzione analitica:
z 1
F z
z 2 1 z 1
1
F x
F x
1
1 x2
1
1 x2
e
e
i
i
0
i 1
2e 2
i
2
i
2e 2
i
x i 2 0 i 2
i
e e
1 x
1 x2
i
i
1 x i 2 2 i 2
e
e
1 x
1 x2
F x
1 x
2 1 x
1 x
i
F x
1 x
1 x2 1 x
i
F x
F x
1
i
2 i 1
cos
i
1
1
i
i
e
e
e
e
e quindi:
74
i
1 x
cos
2 1 x
1 x
2i
2i
1
d
1 2 x
1 x2
1
i
1 x
e
1 x
1 x
sin
2 1 x
1 x
1
1 i
i
1
1
d
1
1 2 x
1 x2
1
i
1 x
e
1 x
i
i
2i
i
1 x
sin
1 x
1 x
tan
1 x
1
i
1
1
2
1
d
2 x
1 2 tan 2 1
1
1
1
i
1 1
1
1
d
2
2 x
1
tan
1
1
1
i
1
1
1
1
1
d
2
2
2 x
1
tan 2
1
tan
1
1
1
i
1
1
2
1
d
2
2
2 x
1 tan 1
1
1
1
i
1 1
1
1
d
2
2 x
1
tan
1
1
1
i
1
1
1
1
1
d
2
2
2
2 x
1
tan
1
tan
1
1
Di conseguenza:
1
i
1
1
2
1
d
2 x
1 2 tan 2 1
1
1
tan i
tan 2 1 x 2
1 x
1 x
i
1
i
1
1
1
1
1
d
2
2
2 x
1
tan 2
1
tan
1
1
75
oppure:
1
i
1
1
1
1
d
2 x
1 2 tan 2 1
1
1
i
1 x
tan
1 x2 1 x
i
1
i
1
1
2
1
2
tan
d
2 x
1 2 tan 2 1
1
1
che, unito al risultato precedentemente ottenuto:
1
i
1
1
2
1
d
2 x
1 2 tan 2 1
1
1
i
2
i
cos
1 x x
tanh
tan
1 x 2 tan 2 1 x 1 x 2
i
1
1
cos
1
1
tanh
d
2
2
tan
1
x
1
tan
1
produce il risultato:
76
1
i
1 1
2
1
d
2
2
1
x
1
tan
1
1
1
1
i
i
1 1 1
1
1 1 1
1
1
d
d
2
2
2
2
tan 1 1 1 x
tan 1 1 1 1 tan x
1
1
i
1 1 i
1 1
2
1
2
1
d
d
2
2
1 1 1 i tan x
1
x
1
tan
1
1
1
77
Per il calcolo di questo integrale di Cauchy, si considera la seguente
funzione analitica F:
1
z 1 z 1
F z
2
2
1 z tan z 1 z 1
i
2
2
z z
i
z
tan
i
1
z 1 z 1 2
1
1
z
2
2
2
1 z tan z 1 z 1
tan tan 2
Si ha:
1
z 1 2
1
F z
2
2
1
1 z tan
z 1 2
F x
i
1
z 1 2
z
z 1
tan 2
1
1 x 2 e 2 e 2 0 1 x ei2 0e i2 x 2 1
1
2
2
1
1 x
1 x tan
tan 2
1 x 2
i
i
i
i
i x2
i cos
i
1 x 1 x
e
2
2
2
tan
1 x tan 1 x 1 x
1 x
i
cos
1
1 x 1 x x 2
e
2
2
2
tan
1 x tan 1 x 1 x
1 x
F x
1
i
i
2
i
i
1 x 2 2 2 2 1 x i i 2 2 i 2 x 2
i cos
1
2
2
e
e
e
e
e
e
1
2
1 x
tan
1 x 2 tan 2
1
x
1 x 2
i
i cos
i
1 x 1 x i x 2
e
2
2
2
tan
1 x tan 1 x 1 x
1 x
i
cos
1
1 x 1 x x 2
e
2
2
2
tan
1 x tan 1 x 1 x
1 x
F x F x
i
1
1 x 1 x
e e
2
2
1 x tan 1 x 1 x
i
x2
1 x2
cos
tan
cos
tan
e e
x
cos
2
1 x 1 x
sinh
cosh
2
tan
1 x tan 1 x 1 x
1 x2
2
2
F x
F x
i
1
1 x 1 x
e e
1 x 2 tan 2 1 x 1 x
i
x2
1 x
2
e e
x
cos
2
1 x 1 x
sinh
cosh
tan
1 x 2 tan 2 1 x 1 x
1 x2
2
i
x2
cos
1
2
1 x 1 x
sinh
cosh
2
2
2
i 1 1 x tan 1 x 1 x
tan
1 x
1
78
79
80