Formulario di Trigonometria
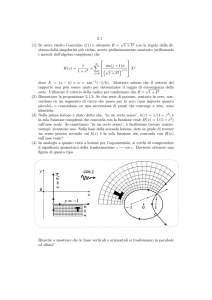
Indice degli argomenti
Formule fondamentali
Valori noti delle funzioni trigonometriche
Simmetrie delle funzioni trigonometriche
Relazioni tra funzioni goniometriche elementari
Formule sugli angoli complementari e supplementari
Formule di addizione e sottrazione
Formule di duplicazione e bisezione
Formule di prostaferesi
Formule parametriche (t
= tan
α
2
)
Formule di Werner
Funzioni goniometriche inverse
Funzioni iperboliche
1
www.webtutordimatematica.it
Formule fondamentali
sin
2
α + cos
tan x =
cot x =
sec x =
csc x =
2
α = 1
sin x
cos x
cos x
sin x
1
cos x
1
sin x
2
www.webtutordimatematica.it
Valori noti delle funzioni trigonometriche
3
www.webtutordimatematica.it
Simmetrie delle funzioni trigonometriche
sin(−x)
= − sin x
cos(−x)
= cos x
tan(−x)
= − tan x
cot(−x)
= − cot x
4
www.webtutordimatematica.it
Relazioni tra funzioni goniometriche elementari
tan α
−
−−−
−−
−−
2
sin α = ±√1 − cos α
sin α = ±
−−−−
−−−−
√1 + tan2 α
−
−
−−
−
−
−−
2
cos α = ±√1 − sin α
cos α = ±
−−−−
−−−−
√1 + tan2 α
−
−
−−
−
−
−−
√1 − sin2 α
−
−
−−
−
−
−−
√1 − sin2 α
cot α = ±
sin α
−
−−−
−−
−−
√1 + cot2 α
cos α = ±
−
−−−
−−
−−
√1 + cot2 α
cot α
1
−
−−−
−−
−−
√1 − cos2 α
sin α
tan α = ±
1
sin α = ±
tan α = ±
1
tan α =
cot α
cos α
cos α
cot α = ±
−
−−−
−−
−−
√1 − cos2 α
5
1
cot α =
tan α
www.webtutordimatematica.it
Formule sugli angoli complementari e supplementari
Angolo
Operatore
π
2
− α
π
2
+ α
π − α
π + α
3π
2
− α
3π
2
+ α
2π − α
sin
cos α
cos α
sin α
− sin α
− cos α
− cos α
− sin α
cos
sin α
− sin α
− cos α
− cos α
− sin α
sin α
cos α
tan
cot α
− cot α
− tan α
tan α
cot α
− cot α
− tan α
cot
tan α
− tan α
− cot α
cot α
tan α
− tan α
− cot α
6
www.webtutordimatematica.it
Formule di addizione e sottrazione
Formule di addizione
sin(α + β) = sin α cos β + cos α sin β
cos(α + β) = cos α cos β − sin α sin β
tan(α + β) =
cot(α + β) =
tan α+tan β
1−tan α tan β
cot α cot β−1
cot β+cot α
Formule di sottrazione
sin(α − β) = sin α cos β − cos α sin β
cos(α − β) = cos α cos β + sin α sin β
tan(α − β) =
cot(α − β) =
tan α−tan β
1+tan α tan β
cot α cot β+1
cot β−cot α
7
www.webtutordimatematica.it
Formule di duplicazione e bisezione
Formule di duplicazione
sin 2α = 2 sin α cos α
cos 2α = cos
tan 2α =
cot 2α =
2
α − sin
2
α
2 tan α
1−tan
cot
2
2
α
α−1
2 cot α
Formule di bisezione
sin
cos
tan
cot
α
2
α
2
α
2
α
2
−−−−−
1−cos α
= ±√
2
−−−−−
1+cos α
= ±√
2
−−−−−
= ±√
1−cos α
1+cos α
−−−−−
= ±√
8
1+cos α
1−cos α
www.webtutordimatematica.it
Formule di prostaferesi
α+β
sin α + sin β = 2 sin
α−β
cos
2
2
α−β
cos
2
α−β
sin
2
α+β
cos α + cos β = 2 cos
α+β
sin α − sin β = 2 cos
2
α+β
cos α − cos β = −2 sin
2
α−β
sin
2
sin(α + β)
2
sin(α − β)
tan α + tan β =
tan α − tan β =
cos α cos β
cos α cos β
sin(β + α)
sin(β − α)
cot α + cot β =
cot α − cot β =
sin α sin β
sin α sin β
9
(
= tan
)
www.webtutordimatematica.it
Formule parametriche (t
α
= tan
sin α =
2
)
2t
2
1+t
2
cos α =
tan α =
1−t
2
1+t
2t
2
1−t
2
cot α =
10
1−t
2t
www.webtutordimatematica.it
Formule di Werner
sin α cos β =
cos α cos β =
sin α sin β =
1
[sin(α + β) + sin(α − β)]
2
1
2
1
2
[cos(α + β) + cos(α − β)]
[cos(α − β) − cos(α + β)]
11
www.webtutordimatematica.it
Funzioni goniometriche inverse
Le funzioni goniometriche inverse sono: arcoseno, arcocoseno, arcotangente e
arcocotangente.
arcsin x = sin
−1
arccos x = cos
x
−1
x
−1
arctan x = tan
arccotx = cot
12
−1
x
x
www.webtutordimatematica.it
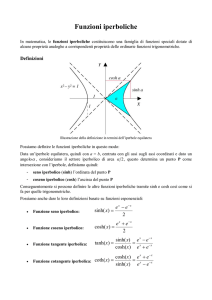
Funzioni iperboliche
Le funzioni iperboliche sono: seno iperbolico, coseno iperbolico, tangente iperbolica,
cotangente iperbolica.
Formule fondamentali
2
cosh
α − sinh
tanh x =
coth x =
sech x =
csch x =
2
α = 1
sinh x
cosh x
cosh x
sinh x
1
cosh x
1
sinh x
Forma esponenziale
Per calcolare il valore delle funzioni iperboliche dobbiamo considerare la loro espressione in
forma esponenziale.
x
sinh x =
e −e
−x
2
x
cosh x =
e +e
−x
2
x
tanh x =
coth x =
e −e
x
e +e
−x
−x
x
−x
x
−x
e +e
e −e
Simmetrie delle funzioni iperboliche
sinh(−x) = − sinh x
cosh(−x) = cosh x
tanh(−x) = − tanh x
coth(−x) = − coth x
Formule di addizione e sottrazione
sinh(α + β) = sinh α cosh β + cosh α sinh β
cosh(α + β) = cosh α cosh β + sinh α sinh β
tanh(α + β) =
tanh α+tanh β
1+tanh α tanh β
sinh(α − β) = sinh α cosh β − cosh α sinh β
cosh(α − β) = cosh α cosh β − sinh α sinh β
tanh(α − β) =
tanh α−tanh β
1−tanh α tanh β
Formule di duplicazione e bisezione
13
www.webtutordimatematica.it
sinh 2α = 2 sinh α cosh α
2
cosh 2α = cosh
α + sinh
1+tanh
α
2
cosh
tanh
α
2
α
2
α
2 tanh α
tanh 2α =
sinh
2
2
α
−−
−−−−
= ±√
cosh α−1
2
−−
−−−−
cosh α+1
= √
2
−−
−−−−
= √
cosh α−1
sinh α
Formule di prostaferesi
α+β
sinh α + sinh β = 2 sinh
α−β
α+β
cosh
sinh α − sinh β = 2 cosh
2
2
α+β
2
α−β
cosh α + cosh β = 2 cosh
cosh
Formule parametriche (t
2
= tanh
2
α+β
cosh α − cosh β = −2 sinh
2
α−β
sinh
α−β
sinh
2
α
2
2
)
sinh α =
2t
2
1−t
2
cosh α =
tanh α =
1+t
2
1−t
2t
2
1+t
Formule di Werner
sinh α cosh β =
cosh α cosh β =
sinh α sinh β =
1
[sinh(α + β) + sinh(α − β)]
2
1
2
1
2
[cosh(α + β) + cosh(α − β)]
[cosh(α − β) − cosh(α + β)]
Funzioni iperboliche inverse
Le funzioni iperboliche inverse sono: settore seno iperbolico, settore coseno iperbolico,
settore tangente iperbolica e settore cotangente iperbolica.
−
−
−−−
2
settsinh x = x log(x + √x + 1)
∀x ∈ R
−
−−−−
2
settcosh x = x log(x + √x − 1)
con x ≥ 1
setttanh x =
settcoth x =
1
2
1
2
log
log
1+x
con − 1 < x < 1
1−x
x+1
con x < −1 e x > 1
x−1
14
www.webtutordimatematica.it