Matematica 1 - Corso di Laurea in Ingegneria
Meccanica
Esercitazioni sugli integrali
28 ottobre 2005
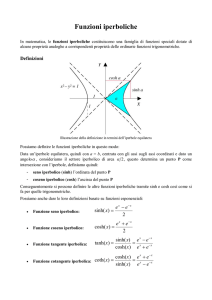
Funzioni iperboliche
Definizione e proprietà generali
Definizione. Le funzioni iperboliche sono definite come
cosh x :=
ex + e−x
,
2
sinh x :=
ex − e−x
,
2
tanh x :=
sinh x
ex − e−x
= x
.
cosh x
e + e−x
Il dominio delle funzioni iperboliche è l’insieme R. Si osservi che cosh
è una funzione pari, mentre sinh e tanh sono dispari. Tutte sono funzioni
continue, anzi derivabili infinite volte.
Esercizio 1. Verificare che:
1. cosh2 x − sinh2 x = 1;
2. cosh(x + y) = cosh x cosh y + sinh x sinh y;
3. sinh(x + y) = sinh x cosh y + sinh y cosh x;
4. cosh(2x) = cosh2 x + sinh2 x = 1 + 2 sinh2 x = 2 cosh2 x − 1;
5. sinh(2x) = 2 sinh x cosh y.
Soluzione. Le prime tre si dimostrano con il calcolo diretto a partire dalla
definizione di cosh e sinh, mentre le ultime due sono una facile conseguenza
delle prime tre. Si noti l’analogia con le funzioni trigonometriche e il fatto che
per ogni x il punto (cosh x, sinh x) appartiene al ramo dell’iperbole equilatera
di equazione x2 − y 2 = 1 con x ≥ 0.
Esercizio 2. Trovare le formule analoghe per tanh(x + y) e per tanh(2x).
1
4
cosh(x)
sinh(x)
tanh(x)
3
2
1
0
-1
-2
-3
-4
-2
-1.5
-1
-0.5
0
0.5
1
1.5
2
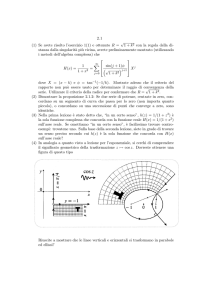
Figura 1: I grafici di cosh, sinh e tanh.
Esercizio 3. Verificare che vale che
1. (D cosh)(x) = sinh x;
2. (D sinh)(x) = cosh x;
3. (D tanh)(x) =
1
cosh2 x
= 1 − tanh2 x.
Soluzione. Le prime due sono immediate applicando le usuali regole di derivazione a partire dalla definizione di cosh e sinh, la terza è una conseguenza
delle prime due e del fatto che cosh2 x − sinh2 x = 1.
Con un semplice studio di funzione si scopre che cosh è decrescente nell’intervallo ] − ∞, 0] e crescente in [0, +∞[, quindi 0 è un punto di minimo
locale. Inoltre limx→±∞ cosh x = +∞. La funzione sinh invece è crescente
su tutto R e limx→±∞ sinh x = ±∞. Anche la funzione tanh è crescente e
limx→±∞ tanh x = ±1. I grafici sono in Figura 1.
Le funzioni inverse
Da quanto detto precedentemente sinh e tanh sono funzioni invertibili, mentre cosh lo è solo come funzione [0, +∞[→ [1, +∞[. Chiameremo la funzione
inversa di cosh, sinh e tanh rispettivamente sett cosh, sett sinh e sett tanh.
2
Osservando che se y = f (x) allora x = f −1 (y) per trovare l’espressione delle
funzioni inverse di rispettivamente cosh, sinh e tanh basta risolvere rispetto
a x le equazioni
y=
ex + e−x
,
2
y=
ex − e−x
,
2
y=
ex − e−x
,
ex + e−x
da cui
e2x − 2yex + 1 = 0,
e2x − 2yex − 1 = 0,
(1 − y)e2x = 1 + y.
Si ottiene
ex = y ±
p
y 2 − 1,
ex = y ±
p
y 2 + 1,
e2x =
1+y
,
1−y
da cui (bisogna osservare che nella prima equazione si esclude la soluzione
con il segno - perché x = sett cosh(y) ≥ 0 per definizione e nella seconda
perché ex > 0)
p
p
1
+
y
1
x = log(y + y 2 − 1), x = log(y + y 2 + 1), x = log
,
2
1−y
cioè
p
y 2 − 1),
p
sett sinh y = log(y + y 2 + 1),
1+y
1
.
sett tanh y = log
2
1−y
sett cosh y = log(y +
Da queste espressioni si potrebbe calcolarne la rispettive derivate con la
formula di derivazione della funzione composta. Si può invece applicare il
1
fatto che (f −1 )0 (y) = f 0 (f −1
e quindi
(y))
1
1
,
=p
sinh(sett cosh y)
y2 − 1
1
1
=p
,
(D sett sinh)(y) =
cosh(sett sinh y)
1 + y2
1
1
(D sett tanh)(y) =
=
.
tanh(sett tanh y)
1 − y2
(D sett cosh)(y) =
3
Applicazioni delle funzioni iperboliche
Le funzioni iperboliche
hanno
√
√ le giuste proprietà per calcolare le primitive di
2
funzioni come x + 1 o x2 − 1.
Abbiamo infatti ponendo x = cosh t
Z √
Z
Z
sinh(2t) t
cosh(2t) − 1
2
x2 − 1 dx = sinh t dt =
dt =
−
2
4
2
1 √ 2
sinh t cosh t t
1
− = x x − 1 − sett cosh(x)
=
2
2
2
2
p
1 √ 2
1
= x x − 1 − log(y + y 2 − 1) + k.
2
2
Ponendo invece x = sinh t
Z √
Z
Z
cosh(2t) + 1
sinh(2t) t
2
2
dt =
+
x + 1 dx = cosh t dt =
2
4
2
√
1
sinh t cosh t t
1
+ = x 1 + x2 + sett sinh(x)
=
2
2
2
2
p
1 √
1
= x 1 + x2 + log(y + y 2 + 1) + k.
2
2
È da osservare√l’analogia √
fra l’uso delle funzioni iperboliche per cercare
una primitiva di x2 + 1 o √x2 − 1 e l’uso delle funzioni trigonometriche
per cercare una primitiva di 1 − x2 . Infatti per fare questa si può porre
x = sin t con t ∈ [− π2 , π2 ] e si ottiene:
Z √
Z
Z
t sin(2t)
1 + cos(2t)
2
2
dt = +
1 − x dx = sin t dt =
2
2
4
√
t sin t cos t
1
1
= +
= arcsin(x) + x 1 − x2 + k.
2
2
2
2
Notare che in questo caso va anche bene la sostituzione x = cos t con t ∈ [0, π]
(fare il conto!).
Esercizio 4. Calcolare l’area del cerchio di equazione x 2 + y 2 ≤ 1.
Il prossimo esercizio dà una interpretazione geometrica delle funzioni
iperboliche.
Esercizio 5. Nel piano cartesiano Oxy si considerino i punti di coordinate
P = (cosh t, sinh t) e Q = (cosh t, − sinh t). Quanto vale l’area compresa fra i
segmenti OP , OQ e l’arco P Q sull’iperbole equilatera di equazione x 2 − y 2 =
1? Quale è il risultato analogo per le funzioni trigonometriche?
4
Altri esercizi
Ricordiamo la formula di integrazione per parti:
Z
Z
0
f (x)g(x) dx = f (x)g(x) − f (x)g 0 (x) dx.
Esercizio 6. Calcolare una primitiva di In =
R
sinn x dx.
Soluzione. Non troveremo una formula esplicita per In , ma una formula che
lega In a In−2 e che ci permette di trovare In in un numero finito di passi.
Integriamo per parti ponendo f 0 (x) = sin x e g(x) = sinn−1 x. Abbiamo:
In =
Z
g0
g
f
f
{ Z z }|
}|
{
{ z
z }| { z }|
n
n−1
n−2
sin x dx = [− cos x][sin
x] − [− cos x][(n − 1) sin
x cos x] dx
Z
= − cos x sinn−1 x + (n − 1) (1 − sin2 x) sinn−2 x dx
= − cos x sinn−1 x + (n − 1)In−2 − (n − 1)In
da cui
1
n−1
In = − cos x sinn−1 x +
In−2
n
n
che è la formula cercata.
(1)
Per fare un paio di esempi, la formula ottenuta di permette di ricondurre
il calcolo di I6 al calcolo di I4 che a sua Rvolta si riconduce al calcolo di I2
a sua volta ricondotta a quella di I0 = sin0 x dx = x + k. Oppure con
questa
R formula possiamo trovare I7 a partire da I5 che si trova sapendo I3 e
I1 = sin x dx = − cos x + k.
Esercizio 7. Calcolare una primitiva di sin7 x, sin6 x, sin5 x, sin4 x, sin3 x e
sin2 x.
R
Esercizio 8. Se chiamiamo Jn = cosn x dx, c’è una formula analoga a (1)
che lega Jn a Jn−2 . Trovarla.
Esercizio 9. Calcolare una primitiva di cos 7 x, cos6 x, cos5 x, cos4 x, cos3 x e
cos2 x.
R
Esercizio 10. Posto In = (1+x1 2 )n dx, trovare la seguente formula:
In =
x
2n − 3
In−1 .
+
2(n − 1)(1 + x2 )n−1 2n − 2
5
Suggerimento. Osservare che
1
x2
1
=
−
(1 + x2 )n
(1 + x2 )n−1 (1 + x2 )n
da cui si ottiene
Z
x2
dx.
(1 + x2 )n
R x2
Infine con un’integrazione per parti calcolare (1+x
2 )n dx.
In = In−1 −
Osservando che I1 = arctan x + k , la formula appena trovata ci permette
di trovare in un numero finito di passi In .
Esercizio 11. Trovare una primitiva di
6
1
.
(1+x2 )3