18. Integrazione per sostituzione
Davide Catania
[email protected]
Esercitazioni di Analisi Matematica 1
A.A. 2016/17
Formula di integrazione per sostituzione. Se ϕ(t) è una
funzione differenziabile con continuità e invertibile, allora
b
Z
a
Z
f (x) dx =
ϕ−1 (b)
ϕ−1 (a)
¡
¢
f ϕ(t) ϕ0 (t) dt ,
con
x = ϕ(t) ,
dx = ϕ0 (t) dt ,
t = ϕ−1 (x) .
Bisogna stabilire la sostituzione x = ϕ(t) più comoda!
Esercizio 1
Z
1
1
p dx =
−1 1 + |x|
Esercizio 2
Calcolapla massa di una sbarra lunga 1 di densità lineare
λ(x) = x x + 1, essendo x la distanza da un estremo.
Esercizio 3
Trova la primitiva F(x) di p
1
x x2 − 1
su ]1, +∞[ tale che F(2) = 0.
Esercizio 4
Z
e2x
dx =
p
ln 2 ex −1
7
Esercizio 5
Z
2
1
dx =
x + e−x
e
−2
Esercizio 6
Z π /2
0
sin3 x cos2 x dx =
Nota. Talvolta è utile effettuare una sostituzione senza
esplicitare x; in tal caso, usiamo
g(x) = t ,
g 0 (x) dx = dt .
È comodo soprattutto se g 0 (x) è già presente nella funzione da
integrare.
Esercizio 7
Z π /4
0
tan x dx =
Sostituzione t = tan x: utile per integrare
¡
¢
f sin2 x, cos2 x, tan x, sin x cos x .
Si usano le formule
sin2 x =
t2
,
1 + t2
cos2 x =
1
.
1 + t2
Esercizio 8
Z π /4
0
tan x
1 + sin2 x
dx =
x
2
Sostituzione t = tan : utile per integrare
f (sin x, cos x) .
Si usano le formule parametriche
sin x =
2t
,
1 + t2
cos x =
1 − t2
.
1 + t2
Esercizio 9
Z π /2
π /3
1
dx =
sin x
Sostituzione f (x) = a sin t : utile per integrare
q
a2 − f (x)2 .
Esercizio 10
p
3/4 p
Z
0
1 − 4x2 dx =
Esercizio 11
Z 1p
3 − 2x − x2 dx =
0
Sostituzione f (x) = a sinh t : utile per integrare
q
a2 + f (x)2 .
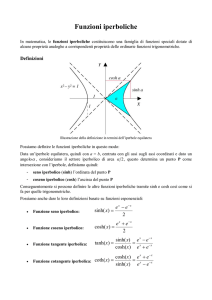
Ricordiamo che, per ogni x ∈ R:
p
1 + sinh2 x = cosh x Ê 1 ,
³
´
p
sinh−1 (x) = ln x + x2 + 1 .
Esercizio 12
Z 1p
1 + x2 dx =
0
Sostituzione f (x) = a cosh t : utile per integrare
q
f (x)2 − a2 .
Ricordiamo che:
p
cosh2 x − 1 = |sinh x|
(x ∈ R) ,
³
´
p
−1
cosh (x) = ln x + x2 − 1
(x Ê 1) .
Esercizio 13
p
Trova la primitiva F(x) di f (x) = x2 + 2x su [0, +∞[ tale che
F(0) = 1.
Riepilogo sulle sostituzioni fondamentali per le radici.
q
a2 − f (x)2
q
a2 + f (x)2
q
f (x)2 − a2
f (x) = a sin t
f (x) = a sinh t
f (x) = a cosh t
Formule utili:
cosh2 x − sinh2 x = 1 ,
´
³
´
³
p
p
cosh−1 x = ln x + x2 − 1 ,
sinh−1 x = ln x + x2 + 1 ,
cosh2 x =
cosh(2x) + 1
,
2
sinh2 x =
cosh(2x) − 1
.
2
Casi immediati.
Z
1
dx = arcsin x + c ,
p
1 − x2
Z
1
dx = sinh−1 (x) + c ,
p
2
1+x
Z
1
dx = cosh−1 (x) + c ,
p
2
x −1
Z
1
dx = arctan x + c ,
1 + x2
Z
1
dx = vedi integrazione di funzioni razionali fratte .
1 − x2
Area dell’ellisse e del cerchio, e definizione di π.
Esercizio 14
Calcola l’area di un’ellisse di semiassi a, b > 0. Deduci la
formula per l’area di un cerchio di raggio r > 0.