FAM
Serie 14: Soluzioni
C. Ferrari
Esercizio 1 Invarianza dell’intervallo
R = Astronave, R′ = Razzo.
1. x0 = 5 m,
2. ∆s2 = −9 m2 ,
3. ∆s′2 = −9 m2 ,
4. ∆~x′ = ~0,
5. ∆x′0 = 3 m.
Esercizio 2 Invarianza dell’intervallo: dimostrazione in 1+1 dimensioni
1.-4. Basta seguire le indicazioni.
5.-6. Abbiamo ∆s′2 = K(k~uk)∆s2 e l’equivalenza dei sistemi di riferimento permette
di scrivere ∆s2 = K(k − ~uk)∆s′2 e dunque K(k~uk)K(k − ~uk) = 1, ossia
K(k~uk)2 = 1 =⇒ K(k~uk) = ±1
ma per ~u = ~0, K(k~uk) deve essere +1 e dunque la sola soluzione possibile è
K(k~uk) = 1.
Osservazione: Per dimostrare il risultato in 1 + 3 dimensioni è sufficiente osservare
che le due equazioni inerenti la propagazione della luce devono valere per ogni coppia
di eventi A e B collegati da un lampo di luce. È quindi sufficiente considerare i tre
casi seguenti:
• A e B sull’asse x′1 quindi si ha ∆x′2 = ∆x′3 = 0 e si ottiene il caso discusso in
questo esercizio.
• A e B sull’asse x′2 quindi si ha ∆x′1 = ∆x′3 = 0 e si ottiene un caso simile a
quello discusso in questo esercizio.
• A e B sull’asse x′3 quindi si ha ∆x′1 = ∆x′2 = 0 e si ottiene un caso simile a
quello discusso in questo esercizio.
1
Esercizio 3 Invarianza dell’intervallo: dimostrazione alternativa di K = 1
1. K(k~u2 k)∆s22 = K(k~u1 k)∆s21 = K(k~u1 k)K(k~u12 k)∆s22
=⇒ K(k~u2 k) = K(k~u1k)K(k~u12 k)
2. Benché non conosciamo (ancora) come esprimere ~u12 in termini dei vettori ~u1
e ~u2 possiamo affermare che la norma di ~u12 dipenderà dalle norme k~u1 k, k~u2k
e dall’angolo θ tra i vettori ~u1 e ~u2 . Quindi
K(k~u12 k) = f (θ, k~u1 k, k~u2k)
ma
K(k~u2 k)
= g(k~u1k, k~u2k)
K(k~u1 k)
3. Ora visto che g non dipende da θ anche f deve essere indipendente da θ e quindi
K(k~u12 k) non può dipendere da k~u12 k ed è dunque costante. In generale quindi
K(k~uk) = costante .
4. Se R = R′ allora K = 1 da cui K = 1.
Esercizio 4 Trasformazioni di Lorentz: struttura di gruppo
1.
γ
−γβ 0 0
−γβ
γ
0 0
L(~u) =
0
0
1 0
0
0
0 1
2. Si verifica che L(−~u)L(~u) = L(~u)L(−~u) = I4
γ γβ
γβ γ
L(−~u) =
0
0
0
0
e che L(~0) = I4 .
dove
0
0
1
0
0
0
0
1
3. Abbiamo (utilizzando le proprietà delle funzioni iperboliche)
cosh(η1 + η2 ) − sinh(η1 + η2 )
cosh η2 − sinh η2
cosh η1 − sinh η1
=
− sinh(η1 + η2 ) cosh(η1 + η2 )
− sinh η2 cosh η2
− sinh η1 cosh η1
da cui, ponendo
u3
c
= tanh η3 = tanh(η1 + η2 ), si ha
tanh η3 =
tanh η1 + tanh η2
1 + tanh η1 tanh η2
e quindi il risultato cercato.
2
4. Senza perdere in generalità possiamo prendiamo come evento A l’evento parametrizzato in R e R′ da (0, 0, 0, 0). Utilizzando la trasformazione di Lorentz
nella direzione 1 possiamo scrivere
′2
′2
′2
2
2
2
2
2
2
∆s′2 = −x′2
0 + x1 + x2 + x3 = −γ (x0 − βx1 ) + γ (x1 − βx0 ) + x2 + x3
= −x20 γ 2 (1 − β 2 ) + x21 γ 2 (1 − β 2 ) + x22 + x23 = ∆s2 .
Esercizio 5 Sistema di riferimento inerziale
1. ∆t = 3,47 · 10−9 s (MRU),
2. ∆x = 6,03 · 10−17 m (MRUA),
3. Sı̀, perché l’effetto della gravità è trascurabile.
Esercizio 6 Il mesone K +
R = Laboratorio, R′ = sistema di riferimento di riposo dei K + .
Calcoliamo il ∆s2 tra gli eventi A e B che corrispondono al passaggio dei K + ai due
contatori: ∆s2 = −26,5 m2 . Da cui (abbiamo ∆~x′ = ~0)
∆t′ = 1,72 · 10−8 s
che sono due tempi di dimezzamento, poiché restano 1/4 delle particelle, quindi
t′1/2 = 8,58 ns.
Esercizio 7 Velocità limite
1. Si verifica facilmente quanto richiesto nei seguenti casi: ~v = (±c,0,0), ~v =
(0, ± c,0) e ~v = (0,0, ± c), con ~u = (±u,0,0). Nei tre casi otteniamo k~v ′ k = c.
È possibile dimostrare in generale che, se ~v = (α1 c,α2 c,α3 c) e quindi
k~vk2 = c2 (α12 + α22 + α32 ) ,
allora (verifica!)
P
• se 3i=1 αi2 = 1 allora k~v ′k2 = c2 per ogni ~u (di norma inferiore a c)
P
• se 3i=1 αi2 < 1 allora k~v ′k2 < c2 per ogni ~u (di norma inferiore a c) .
2. A causa dell’indice di rifrazione la velocità della luce in acqua è minore di c.
3
Esercizio 8 Composizione delle velocità
R = Laboratorio, R′ = K + .
• Caso NR:
v1 = v1′ + u = ±0,72c + 0,998c =
(
1,718c
0,278c
a dipendenza se il verso del moto del µ+ è uguale o opposto al verso del moto
del K + . Con la teoria NR si ottengono velocità superiori a c quindi la teoria
newtoniana è sicuramente inapplicabile per particelle la cui velocità è prossima
a quella della luce.
• Caso RR:
v′ + u
±0,72 + 0,998
v1 = 1 ′ = 1 ± 0,7185 c =
v u
1 + 12
c
(
0,9997c
0,988c
Esercizio 9 Aberrazione della luce ricevuta dalle stelle fisse
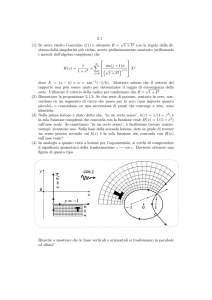
R = Stella, R′ = Terra (T). Il piano dell’eclittica è il piano dell’orbita terrestre.
α
~v
~v ′
α
x2
x1
x3
T
~u
~v = (0, − c, 0), utilizzando la legge di p
composizione delle velocità otteniamo la
′
velocità rispetto alla Terra ~v = (−u, − c 1 − β 2 , 0) da cui
u
tan α = p
.
c 1 − β2
Osservazioni:
L’osservatore sulla Terra vede la stella con un’angolo α rispetto alla verticale. Per
effetto della velocità relativa tra un astro e l’osservatore terrestre (dovuto alla rivoluzione della Terra intorno al Sole), la direzione da cui sembra provenire la luce
dell’astro non coincide con la direzione vera, cosicchè una stella od un altro corpo
celeste, sono visti in posizioni che generalmente non sono quelle reali. Ciò causa una
leggera variazione apparente, sulla direzione di arrivo della luce, e quindi un’errata
determinazione della posizione di un corpo celeste. Questo fenomento è noto come
aberrazione stellare.
4
Lo scostamento apparente della posizione vera varia periodicamente, con periodo
di un anno; questo a causa della velocità della Terra intorno al Sole che varia con
il variare della distanza da esso. Tale fenomeno fu scoperto dall’astronomo inglese
James Bradley (1693–1762), nel 1728 osservando la stella Eltanin (γ–Draconis); e
fornı̀ una prova convincente della rivoluzione annua della Terra intorno al Sole. Inoltre, l’osservazione dell’aberazione stellare permette di conculdere che, se il presunto
etere esistesse, esso allora non è trascinato dal moto della Terra (ipotesi alla base
dell’esperienza di Michelson e Morley).
5