Nome…………………….Cognome………………….
12 Febbraio 2009
Classe 4D
VERIFICA di MATEMATICA
Problemi
7
4
1) Nel triangolo ABC si sa che cos BAˆ C =
, tan ABˆ C =
e CM = a , essendo CM l’altezza relativa
25
3
ad AB. Determinare le misure dei lati del triangolo.
2) Nel triangolo ABC si sa che AB = a e BAˆ C = 3 ABˆ C . Conduci una semiretta r avente origine A, che
incontri il lato BC in P e tale che BAˆ P = PBˆ A . Posto ABˆ C = x , determina l’espressione di
AP
BH
f ( x) =
+3
+ 2 essendo BH la distanza di B dalla semiretta r. Traccia il grafico della
2 AC
AP
funzione trovata.
3) Sia ABC un triangolo equilatero di lato 2l. Considera un punto P Sulla semicirconferenza di diametro
2
BC, esterna al triangolo. Determina in funzione di x = PBˆ C l’espressione di: f ( x) = AP + AB ⋅ PH ,
essendo PH la distanza di P dalla retta BC. Qual è il massimo valore di f(x) ?
4) Sia M il punto medio del segmento AB = 2a . In uno dei due semipiani da AB, si fissi un punto P tale
3
che cos( APˆ M ) = . Posto PAˆ M = x , determina per quali valori 5 AP + PM = 5a .
5
Disequazioni
x
+ sin x
2
<0
tgx + 1
2 cos 2
1)
2)
3 sin 2 x − cos 2 x
≤0
2 cos 2 x − 3 cos x + 1
3) sin x − cos x < 1
Grafici
Per ciascuna delle seguenti funzioni traccia il grafico e determina massimo e minimo (quando esistono)
1) y =
2 sin 2 x + sin x − 3
1 − sin x
2) y = 2 cos 2 x − 3
Verifica di trigonometria 12 febbraio
3) y = cos(2 x) − 3 sin(2 x) − 1
1
Soluzioni verifica di matematica 4D 12 febbraio 2009
Problema 1
7
4
, tan ABˆ C =
e CM = a , essendo CM l’altezza relativa ad
Nel triangolo ABC si sa che cos BAˆ C =
25
3
AB. Determinare le misure dei lati del triangolo.
Utilizzando la calcolatrice è possibile vedere che BAˆ C ≈ 73°,7 e ABˆ C ≈ 53°,1 e quindi fare il disegno
corrispondente.
C
AC =
CM
sin BAˆ C
AM =
CM
(CMA rettangolo)
tan BAˆ C
BC =
CM
sin ABˆ C
BM =
CM
(CMB rettangolo)
tan ABˆ C
a
A
B
M
Dalle relazioni tra funzioni goniometriche:
sin BAˆ C 24
24
tan ABˆ C
4
sin BAˆ C = 1 − cos 2 BAˆ C =
;
; sin ABˆ C =
=
tan BAˆ C =
=
25
7
cos BAˆ C
1 + tan 2 ABˆ C 5
25
5
7
3
25
quindi: AC =
a ; BC = a ; AM =
a ; BM = a ; AB =
a
24
4
24
4
24
Problema 2
Nel triangolo ABC si sa che AB = a e BAˆ C = 3 ABˆ C . Conduci una semiretta r avente origine A, che
incontri il lato BC in P e tale che BAˆ P = PBˆ A . Posto ABˆ C = x , determina l’espressione di
AP
BH
+3
+ 2 essendo BH la distanza di B dalla semiretta r. Traccia il grafico della funzione
f ( x) =
2 AC
AP
trovata.
C
H
P
3x
A
Posto ABˆ C = x si ha 0 < x <
a
interni di un triangolo è π )
x
π
(poiché la somma degli angoli
4
B
BH = AB sin x = a sin x (AHB rettangolo)
AB
a
AP =
=
(APB isoscele)
2 cos x 2 cos x
AB
a sin x
AC =
sin x =
(ABC)
sin(π − 4 x)
sin(4 x)
sin( 4 x)
+ 6 sin x cos x + 2 .
4 cos x sin x
Ricordando la formula di duplicazione del seno si può scrivere: sin(4 x) = sin(2 ⋅ 2 x) = 2 sin(2 x) cos(2 x)
2 sin(2 x) cos(2 x)
f ( x) =
+ 3 sin(2 x) + 2 = cos(2 x) + 3 sin(2 x) + 2 .
2 sin(2 x)
Sostituendo nella relazione, semplificando il parametro a si ottiene: f ( x) =
Verifica di trigonometria 12 febbraio
2
Utilizzando il metodo dell’angolo aggiunto si ha:
1
1
1
1
f ( x) = 10 cos(2 x − arccos
) + 2 = 10 cos 2( x − arccos
) + 2 ( arccos
≈ 71°,7 )
2
10
10
10
Il grafico si ottiene con i seguenti passaggi:
y
5
disegno il grafico di cosx,
4
contraggo orizzontalmente di 2
sposto a sinistra l’asse verticale
1
1
arccos
2
10
3
dilato verticalmente di 10
2
abbasso l’asse orizzontale di 2
1
x
−π
−3π/4
−π/2
−π/4
di
π/4
π/2
3π/4
massimo: 10 + 2
minimo: − 10 + 2
π
−1
Problema 3
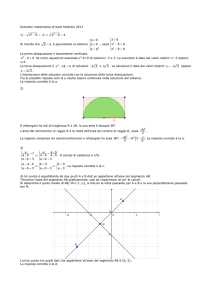
Sia ABC un triangolo equilatero di lato 2l. Considera un punto P Sulla semicirconferenza di diametro BC,
2
esterna al triangolo. Determina in funzione di x = PBˆ C l’espressione di: f ( x) = AP + AB ⋅ PH , essendo
PH la distanza di P dalla retta BC. Qual è il massimo valore di f(x) ?
A
l
H
B
π
2
PB = BC cos x = 2l cos x (PBC rettangolo)
PH = PB sin x = 2l cos x sin x (PBH rettangolo)
2
2
2
π
AP = AB + PB − 2 AB ⋅ PB cos + x =
3
(PAB)
π
2
2
2
2
= 4l + 4l cos x − 8l cos x ⋅ cos + x
3
Posto x = PBˆ C si ha: 0 ≤ x ≤
C
x
P
Sostituendo nella funzione di ha:
π
f ( x) = 4l 2 + 4l 2 cos 2 x − 8l 2 cos x ⋅ cos + x + 4l 2 cos x sin x =
3
1
3
= 4l 2 + 4l 2 cos 2 x − 8l 2 cos x ⋅ cos x −
sin x + 4l 2 cos x sin x =
2
2
(
)
(
)
= 4l 2 + 4 1 + 3 l 2 sin x cos x = 4l 2 + 2 1 + 3 l 2 sin(2 x)
(
)
f ( x) = 4l 2 + 2 1 + 3 l 2 sin(2 x) avrà massimo pari a
π
f ( x) = 2 3 + 3 l 2 quando sin(2 x) = 1 , cioè solo in x = (tenendo conto delle limitazioni)
4
Senza bisogno di disegnarla, la funzione
(
)
Verifica di trigonometria 12 febbraio
3
Problema 4
Sia M il punto medio del segmento AB = 2a . In uno dei due semipiani da AB, si fissi un punto P tale che
3
cos( APˆ M ) = . Posto PAˆ M = x , determina per quali valori 5 AP + PM = 5a .
5
Utilizzando la calcolatrice APˆ M = γ ≈ 53° e dalle relazioni tra le funzioni goniometriche: sin( APˆ M ) =
Posto PAˆ M = x si ha: 0 ≤ x ≤ π − γ
P
AP =
γ
A
x
a
M
5 AP + PM = 5a
4
5
B
a
AM
5a
sin(π − ( x + γ )) =
sin( x + γ ) (APM)
sin γ
4
AM
5a
sin x =
sin x (APM)
sin γ
4
Sostituendo nella relazione si ha:
MP =
25
5
a sin( x + γ ) + a sin x = 5a utilizzando la formula di addizione del seno:
4
4
⇒
5 3
4
1
( sin x + cos x) + sin x = 1 ; sin x + cos x = 1 si ottiene così un’equazione lineare che si può risolvere
4 5
5
4
con il metodo della circonferenza:
Y = − X + 1
2
X + Y 2 = 1
di
conseguenza
x=0 ∨ x=
si
hanno
le
π
2
soluzioni:
x = 2kπ ∨ x =
π
+ 2kπ
2
,
accettabili
sono
solo
x
+ sin x
2
Disequazione 1
<0
tgx + 1
La disequazione è fratta, si studiano quindi separatamente numeratore e denominatore:
x
cos x + 1 + sin x > 0
2 cos 2 + sin x > 0
utilizzando la formula di bisezione:
2
tan x > −1
tan x > −1
La
prima
disequazione è lineare, si può risolvere facilmente con il metodo della
circonferenza:
2 cos 2
Y > − x − 1
2
X + Y 2 = 1
quindi la soluzione è:
Verifica di trigonometria 12 febbraio
4
π
3
+ 2kπ < x < π + 2kπ
2
4
∨ π + 2kπ < x <
7π
3
+ 2kπ ∧ x ≠ π + 2kπ
4
2
3 sin 2 x − cos 2 x
≤0
2 cos 2 x − 3 cos x + 1
La disequazione è fratta, si studiano quindi separatamente numeratore e
denominatore:
Disequazione 2
3 sin 2 x − cos 2 x ≥ 0
2 cos 2 x − 3 cos x + 1 > 0
la prima disequazione è omogenea, la seconda è di 2° grado in cosx:
3 tan 2 x − 1 ≥ 0 ⇒ tan x ≤ −
cos x <
3
3
∨ tan x ≥
3
3
1
∨ cos x > 1
2
La soluzione è:
π
1
+ 2kπ < x < π + 2kπ
6
3
∨
5
7π
π + 2kπ < x <
+ 2kπ
6
6
5
11
π + 2kπ < x ≤ π + 2kπ
3
6
∨
Disequazione 3 sin x − cos x < 1
La disequazione con il modulo è equivalente a: − 1 < sin x − cos x < 1 ,
sin x > cos x − 1
,
cioè si tratta di un sistema di due disequazioni lineari:
sin x < cos x + 1
Y > X − 1
risolvendolo con il metodo della circonferenza si ha: Y < X + 1
2
2
X + Y = 1
π
La soluzione è: kπ < x < + kπ
2
2 sin 2 x + sin x − 3
per disegnare la funzione è necessario 1
1 − sin x
semplificare, eseguendo per esempio la divisione con la regola di Ruffini.
Si ottiene quindi:
y
3
2 sin 2 x + sin x − 3 (2 sin x + 3)(sin x − 1)
y=
=
= −2 sin x − 3
1 − sin x
− (sin x − 1)
2
Grafico 1
y=
π
Con la condizione x ≠ + 2kπ .
2
Il grafico si ottiene con i seguenti passaggi:
traccio il grafico di sinx,
dilato verticalmente di 2
faccio il simmetrico rispetto all’asse delle
ascisse,
alzo l’asse orizzontale di 3
Verifica di trigonometria 12 febbraio
2
1
2
-3
3
2
3
0
1
x
−2π
−3π/2
−π
−π/2
−1
π/2
π
3π/2
−2
−3
−4
−5
−6
−7
−8
−9
5
2π
data la C.E. elimino i punti corrispondenti a
massimo:-1
minimo: non c’è
x=
π
+ 2kπ
2
Grafico 2 y = 2 cos 2 x − 3
Occorre prima abbassare di grado, utilizzando le formule di duplicazione:
1 + cos(2 x)
y= 2
− 3 = cos(2 x) − 2
5
2
y
4
3
Il grafico si ottiene con i seguenti passaggi:
2
disegno il grafico di cosx,
contraggo orizzontalmente di 2
alzo l’asse orizzontale di 2
ribalto le parti negative (cioè tutto)
1
x
massimo: 3
−π
minimo: 1
−π/2
π/2
π
−1
−2
−3
Grafico 3 y = cos(2 x) − 3 sin(2 x) − 1
Occorre prima utilizzare il metodo dell’angolo aggiunto per riscrivere la somma di seno e coseno:
π
π
y = 2 cos(2 x + ) − 1 = 2 cos 2( x + ) − 1
3
6
y
2
Il grafico si ottiene con i seguenti passaggi:
1
x
−π
−2π/3
−π/3
π/3
−1
−2
2π/3
π
disegno il grafico di cosx,
contraggo orizzontalmente di 2
dilato verticalmente di 2
sposto l’asse verticale a destra di
π
6
alzo l’asse orizzontale di 1
massimo: 1
minimo: -3
−3
−4
Verifica di trigonometria 12 febbraio
6