Preparazione_verifica_di_aprile

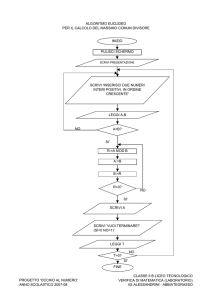
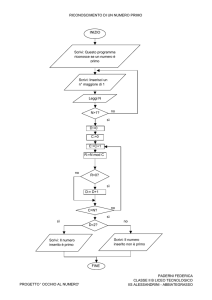
Funzioni:
 Scrivi la funzione il cui grafico sia una retta orizzontale passante per il punto (2,7)
 Scrivi una funzione il cui grafico sia una retta che passa per il punto (0, -1) e parallela al grafico della
funzione y=3x
 Scrivi una funzione il cui grafico sia una parabola con asse di simmetria coincidente con l’asse y, il vertice
nel punto (0,-2) e la con la concavità rivolta verso l’alto.
 Disegna i grafici di ciascuna delle funzioni precedentemente trovate e stabilisci quali di esse sono
biunivoche, motivando la tua risposta.
Divisioni tra polinomi:
 Esegui la seguente divisione e verifica il risultato trovato: x 4  2x 3  2x 2  5: x 2  x  4
 Dato il polinomio 6 x 3  5x 2  x  12 , stabilisci se esso è divisibile per i seguenti binomi: x  1, x  1
Espressioni:

x 2 1
x  2 1  2 x 3  x 2


  2
;
 x 3  x 2  4x  4 x
x  2 x  3x  2





  x3
x
2  2

x

x

2

1
 0, 3 

 3
  
2
3

 x  3x  3x  2 x  1 
  3

Geometria:
 Internamente al lato AB del triangolo ABC si riportino tre segmenti adiacenti AD, DE, EF qualsiasi. Si
dimostrino le seguenti disuguaglianze: ADˆ C  AEˆC; ADˆ C  ABˆ C; AEˆC  ECˆF; AEˆC  EBˆ C
 Dimostrare che in un triangolo acutangolo la somma delle tre altezze è minore del perimetro e maggiore del
semiperimetro.
 In ogni triangolo la congiungente un vertice con un punto qualunque del lato opposto è minore di uno
almeno degli altri due lati.