Nome……………………..Cognome……………………. Classe…….
14 Marzo 2011
Verifica di fine corso
A) Risolvi le seguenti disequazioni:
x
≤0
2
1)
π
1
sin( x − ) <
4
3
3)
2)
3 cos x + sin x
≤0
cos x − sin x
4)
sin x + 2 cos x ≥ cos x + 1
3 sin x − sin
B) Traccia i grafici delle seguenti funzioni per ciascuna indica:
- se è periodica, il periodo
- le intersezioni con gli assi cartesiani.
1) y =
2 − cos 2 x
3
2) y = sin( x −
π
)
6
C) Risolvi il seguente problema
E’ dato il quadrilatero ABCD inscritto in una circonferenza di raggio r. L’angolo in A è di
che ABˆ D = 2 DBˆ C . Posto DBˆ C = x , determina
AB BC
3
f ( x) =
+
. Risolvi quindi la disequazione f ( x) <
2
AD DC
tale
l’espressione
analitica
π
, quello in B è
3
della funzione
Soluzioni verifica di fine corso
A) Risolvi le seguenti disequazioni:
x
≤0
2
1)
Per risolvere la disequazione è necessario avere per tutte le funzioni goniometriche lo stesso argomento,
x
meglio usare la formula d duplicazione e vedere sin x = sin 2 ⋅ piuttosto che quella di bisezione che
2
1 − cos x
x
contiene la radice sin = ±
2
2
La disequazione diventa quindi:
x
x
x
x
x
x
3 sin x − sin ≤ 0 ⇒ 6 sin cos − sin ≤ 0 ⇒ sin (6 cos − 1) ≤ 0
+
2
2
2
2
2
2
x
sin ≥ 0
2
Studiando il segno dei due fattori si ha:
⇒
x 1
cos ≥
2 6
+
1
x
1
x
Quindi arccos + 2kπ ≤ ≤ π + 2kπ ∨ − arccos + 2kπ ≤ ≤ 2kπ
6
2
6
2
moltiplicando tutto per 2 si ottiene la soluzione:
1
1
2 arccos + 4kπ ≤ x ≤ 2π + 4kπ ∨ − 2 arccos + 4kπ ≤ x ≤ 4kπ
6
6
3 cos x + sin x
≤0
2) cos x − sin x
Si studia il segno di numeratore e denominatore, entrambe disequazioni
lineari omogenee
cos x = X
sin x ≥ − 3 cos x
, considerata la
⇒ fatta la sostituzione
sin x < cos x
sin x = Y
+
3 sin x − sin
circonferenza goniometrica si ha:
Y ≥ − 3X
Y<X
⇒
-
La soluzione è quindi:
sin( x −
3)
π
4
+
)<
π
2
+ kπ ≤ x ≤ π + kπ
4
3
1
3
1
π − arcsin
π
1
3
E’ una disequazione elementare in α = x −
sin α <
4
3
Guardando la circonferenza goniometrica:
Considerando solo angoli del primo giro si ha
1
1
2kπ ≤ α ≤ arcsin + 2kπ ∨ π − arcsin + 2kπ ≤ α ≤ 2π + 2kπ oppure
3
3
1
1
sul primo e secondo giro: π − arcsin + 2kπ ≤ α ≤ 2π + arcsin + 2kπ quindi
3
3
5
1
9
1
π − arcsin + 2kπ ≤ x ≤ π + arcsin + 2kπ
4
3
4
3
4) sin x + 2 cos x ≥ cos x + 1
arcsin
1
3
E’ una disequazione irrazionale, è quindi necessario mettere le C.E. e, per poter elevare alla seconda le
condizioni di concordanza
sin x + 2 cos x ≥ 0 C.E.
sin x + 2 cos x ≥ 0 C.E.
∨
C.C.
cos x + 1 ≥ 0
∅
cos x + 1 < 0
2
sin x + 2 cos x ≥ cos x + 1 + 2 cos x
sin x + 2 cos x ≥ 0
∀x
2
sin x ≥ 1 − sin x + 1
π
x = + 2kπ
2
sin x + 2 cos x ≥ 0
2
π
sin x + sin x − 2 ≥ 0 ⇒ sin x ≤ −2 (imp ) ∨ sin x ≥ 1 x = 2 + 2kπ
B) Traccia i grafici delle seguenti funzioni per ciascuna indica:
- se è periodica, il periodo
- le intersezioni con gli assi cartesiani.
2 − cos 2 x
3
Per tracciare il grafico bisogna abbassare di grado utilizzando le formule di duplicazione:
1 + cos(2 x)
2−
1 1
2
y=
= − cos(2 x)
3
2 6
Dal grafico del coseno si ottiene con le seguenti trasformazioni,
- contrazione orizzontale di 2 e verticale di 6
- simmetria rispetto all’asse delle ascisse
1
- traslazione verticale di
2
1) y =
y
1.0
0.5
x
−π/4
π/4
π/2
3π/4
π
5π/4
−0.5
−1.0
La funzione è periodica di periodo π
1
3
Dal grafico si deduce che non ci sono intersezioni con l’asse delle ascisse.
L’intersezione con l’asse delle ordinate è y (0) =
π
)
6
Dal grafico del seno si ottiene con le seguenti trasformazioni,
- modulo sulle x, cioè si prendono i punti con le x positive o nulle più i corrispondenti simmetrici rispetto
all’asse delle ordinate
2) y = sin( x −
- traslazione orizzontale del grafico a destra di
π
6
y
2
1
x
−3π/2
−π
−π/2
π/2
π
3π/2
2π
−1
−2
La funzione NON è periodica.
L’intersezione con l’asse delle ordinate è y (0) =
1
2
π
+ kπ k ∈ Z oppure si trovano
6
π
π
π
π
risolvendo l’equazione sin x − = 0 ⇒ x − = kπ ⇒ x − = kπ x = + kπ
6
6
6
6
Dal grafico si deduce che le intersezioni con l’asse delle ascisse sono x =
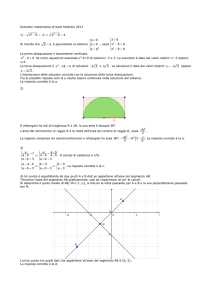
C) Risolvi il seguente problema
π
, quello in B
3
è tale che ABˆ D = 2 DBˆ C . Posto DBˆ C = x , determina l’espressione analitica della funzione
AB BC
3
f ( x) =
+
. Risolvi quindi la disequazione f ( x) <
2
AD DC
E’ dato il quadrilatero ABCD inscritto in una circonferenza di raggio r. L’angolo in A è di
D
C
A
π
3
Ricordando che angoli alla circonferenza che insistono sulla stessa
)
2π
corda, da parti opposte sono supplementari si ha DCB =
,
3
)
2π
π
quindi: BDC = π − ( + x) = − x
3
3
)
π
2π
BDC = π − ( + 2 x) =
− 2x
3
3
Limitazioni: 0 < x <
2π
3
π
3
x
2x
B
Utilizzando il teorema della corda si ottiene:
2π
π
AB = 2r sin( − 2 x) ; AD = 2r sin(2 x) BC = 2r sin( − x) e DC = 2r sin x
3
3
2
π
3
1
3
1
sin( π − 2 x) sin( − x)
cos(2 x) + sin( 2 x)
cos x − sin x
3
3
3
3
2
2
f ( x) =
+
= 2
+ 2
=
cot an 2 (2 x) +
cot anx
sin(2 x)
sin x
sin(2 x)
sin x
2
2
3
3
3
3
significa quindi
cot an(2 x ) + cot anx < 1 o equivalentemente
cot an(2 x ) +
cot anx <
2
2
2
2
1
1
+
< 1 utilizzando le formule di duplicazione si ottiene:
tan(2 x ) tan x
f ( x) <
1 − tan 2 x + 2 − 2 tan x
tan 2 x + 2 tan x − 3
<0
> 0 , considerando le
2 tan x
2 tan x
limitazioni il denominatore è positivo e si può eliminare, rimane così:
tan 2 x + 2 tan x − 3 > 0 ⇒ tan x < −3 ∨ tan x > 1 tenendo conto delle
π
π
limitazioni si ottiene:
<x<
4
3